在复合应力下工作的零件危险截面上同时存在σ、τ，应采用相应的强度理论进行计算。
对塑性材料零件的疲劳强度应按第三强度理论进行计算。
设σ、τ循环周期相同，近似取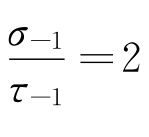
，根据第三强度理论强度条件有
即
将式（2-17）代入上式，并近似取
，即得到安全系数形式的强度条件为
式中 Sσ——只考虑σ时的安全系数，Sσ=σ-1/（Kσσa）；
Sτ——只考虑τ时的安全系数，Sτ=σ-1/（Kτσa）。
为了防止零件产生塑性变形，还应按式（2-26）进行静强度计算：
对于低塑性材料和脆性材料零件，建议由下式计算其疲劳强度：(www.xing528.com)
式中各符号含义同前。
2）非对称循环时复合应力下机械零件的疲劳强度计算
式（2-25）是按对称循环应力得到的，但因非对称循环应力可以折算成当量对称循环应力，所以非对称循环时复合应力下，塑性材料机械零件的疲劳强度仍可按式（2-25）计算，但式中Sσ、Sτ应按单向应力状态下非对称循环时的式（2-18）确定；低塑性材料和脆性材料零件的疲劳强度仍按式（2-27）计算。
以上的讨论是针对零件的无限寿命进行的，即零件的工作应力循环次数N≥N0。当零件在有限寿命期内（N＜N0）工作时，其疲劳强度仍可按以上各式计算，但需要将各式中σ-1换为σ-1N=KNσ-1。
例2-1 一根圆形拉杆如图2-11所示，D=70 mm，d=50 mm，r=5 mm。工作中受脉动循环拉力F=0～3×105N的作用，材料为40Mn钢，σb=750 MPa，σs=500 MPa，轴表面经过精车加工，硬度为250 HBW，工作应力循环次数不低于5×105。规定［S］=1.9，试校核拉杆的强度。
图2-11 圆形拉杆
解：计算过程见表2-12。
表2-12 校核拉杆强度计算
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
