稳定变应力下机械零件疲劳强度的计算

机械零件的疲劳强度常采用安全系数法进行计算。零件的疲劳强度条件为

式中　S——零件实际工作安全系数；

［S］——对疲劳强度规定的许用安全系数，可查阅有关设计资料选定。

零件的极限应力根据不同的循环特性由零件的极限应力线图确定；零件的最大工作应力σmax由力学方法计算。

单向应力状态时零件工作应力只有σ（或τ）。

1）对称循环的疲劳强度计算

零件的疲劳强度条件为

2）非对称循环的疲劳强度计算

在进行非对称循环的疲劳强度计算时，需要确定零件的极限应力。在非对称循环时零件的极限应力还与零件的应力变化规律有关，在不同的应力变化规律下，零件的极限应力有所不同。典型的零件应力变化规律有三种情况：①变应力的循环特性保持不变，即r=C，如绝大多数转轴中的应力情况；②变应力的平均应力保持不变，即σm=C，如振动中的受载弹簧的应力情况；③变应力的最小应力保持不变，即σmin=C，如紧连接螺栓中螺栓受轴向工作变载荷时的应力情况。以下分别进行介绍。

（1）r=C的情况。在图2-8中，设零件的工作应力点为位于区域内，其循环特性r=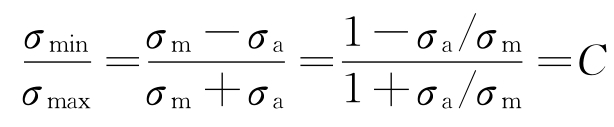，即需σa/σm为一个常数C′。连OM交A′E′于，因为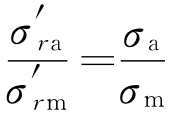为同一常数C′，所以极限应力点与工作应力点M的循环特性相同。

图2-8　r=C时零件的极限应力

A′E′的方程与直线MM′的方程可求出零件的极限应力为

此时，若零件发生破坏，则将疲劳破坏。

将上式代入式（2-16），即得到r=C时零件的疲劳强度条件为

若零件的工作应力点N（σm，σa）位于QE′S区域内，连ON交E′S于，由前可得到零件的极限应力为。此时，若零件发生破坏，则将为塑性屈服。所以，零件的强度条件为

综上所述，在r=C的情况下进行零件的疲劳强度计算时，应首先确定零件的变应力所在的区域。如果工作应力点位于OA′E′范围内，零件将发生疲劳破坏，应按式（2-18）进行计算；如果工作应力点位于OE′S范围内，零件将发生塑性屈服，则应按式（2-19）进行计算。另外，当工作应力点位于OE′直线附近时，零件可能发生疲劳破坏，也可能发生塑性屈服，应同时用式（2-18）和式（2-19）进行计算。

（2）σm=C的情况。在图2-9中，设零件的工作应力点为M（σm，σa）位于OA′E′F区域内。过点M作横轴的垂线交A′E′于，有，即M与M′平均应力相等。所以，在σm=C的情况下，得到点M的极限应力为M′。(www.xing528.com)

同前，可求出零件的极限应力为

将上式代入式（2-16），即得到σm=C时零件的疲劳强度条件为

若零件的工作应力点N（σm，σa）位于FE′S区域内，其极限应力点为N′，零件的极限应力为，强度条件仍为式（2-19），只需进行静强度计算。

若只考虑工作应力中的变化部分，即应力幅对疲劳强度影响时，有应力幅安全系数的强度条件为

式中　Sa——应力幅工作安全系数；

［Sa］——对疲劳强度规定的许用应力幅安全系数。

（3）σmin=C的情况。在图2-10中，设零件的工作应力点为M（σm，σa），位于OA′E′F区域内。过点M作与横轴夹角45°的直线交A′E′于，此时M与M′的最小应力相等。所以，在σmin=C的情况下，得到点M的极限应力为M′。

图2-9　σm=C时零件的极限应力

图2-10　σmin=C时零件的极限应力

同前，可求出零件的极限应力为

点M的最大应力为σmax=σm+σa=2σa+σmin，将其与上式一起代入式（2-16），即得到σmin=C时零件的疲劳强度条件为

若零件的工作应力点N（σm，σa）位于HE′S区域内，其极限应力点为N′，零件的极限应力仍为屈服极限σs，所以只需进行静强度计算。

同前，只考虑应力幅对疲劳强度的影响时，有应力幅安全系数的强度条件为

应注意，在具体设计零件时，当难以确定零件的应力变化规律时，往往取r=C的情况进行疲劳强度计算。

以上讨论的结果同样适用于切应力，只需将各式中的σ换为τ即可。

在进行零件的疲劳强度计算时，若取应力比例系数μ0作图，也可用图解法求解。如在图2-8中，可得到零件的疲劳强度条件为