正弦量相位表示法

1.复数和常用的表示方法

如图3-32所示，向量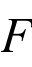复数代数表达示为，式中为虚单位（与数学中常用的i等同）。图中表示复数的大小，称为复数的模，、为复数的实部和虚部。有向线段与实轴正方向间的夹角，称为复数的幅角，用表示，规定幅角的绝对值小于180°。

图3-32　复数坐标

由图可得复数的代数式转化为三角形式：

根据欧拉公式，将复数的三角形式转化为指数形式：

还有极坐标形式：

实部相等、虚部大小相等而异号的两个复数叫作共轭复数，用F* 表示F的共轭复数，则有。

复数可以进行四则运算。两个复数进行乘除运算时，可将其化为指数形式或极坐标形式来进行计算。

如将两个复数相除得

如将复数乘以另一个复数ejωt，

则得

如两个复数进行加减运算时，用代数形式计算。

也可以按平行四边形法则在复平面上作图求得。如图3-33所示。

图3-33　平行四边形法则

2.相量的基本概念

一个正弦量由它的振幅、初相和角频率来确定，其一般表达式为

在正弦稳态电路分析中，各正弦量的角频率都相同，等于交流电源的角频率。正弦量可以用相应的复数来表示，这就是所谓的相量；正弦量的运算可以用相量运算来代替，使交流电路获得一种类似直流电阻电路的简便计算方法。

与正弦量相对应的复指数函数在复平面上可用旋转相量表示出来，正弦量是旋转相量在旋转过程中在正实轴上的投影。其波形如图3-34所示。

图3-34　旋转相量在实轴上的投影对应正弦波

两个同频率正弦量的旋转相量，其角速度相同，旋转相量的相对位置保持不变（同频率正弦量的相位差为常量）。因此，当讨论两个正弦量的振幅和相位关系时，无须考虑它们在旋转，通常只需画出它们在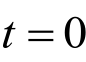时的位置就可以了，即画出它们的相量图，就完全可以比较他们的振幅大小及相位关系。

3.电阻元件伏安关系的相量形式

（1）电阻元件的电压与电流相量关系

如图3-35（a）所示的电阻元件电路

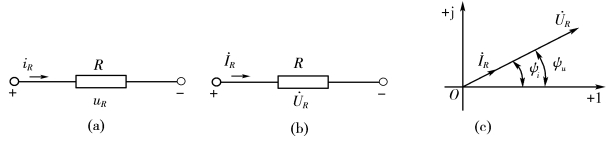
图3-35　电阻元件伏安关系的相量形式

当电阻元件流过正弦电流时，稳态下的伏安关系为：

是同频率的正弦量，其相量形式为

式（3-32）是电阻元件伏安关系的相量形式，由此我们可得出

①，即电阻电压有效值等于电流有效值乘以电阻值。

②，即电阻上电压与电流同相位。

（2）电阻电路的功率

在任一瞬间，电阻两端电压瞬时值与流过电流瞬时值的乘积称为瞬时功率，用小写字母p表示。波形如图3-36所示

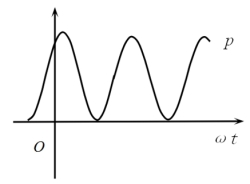
图3-36　功率曲线

由瞬时功率的表达式及曲线图2.12可知，p≥0，表明电阻元件在除过零点的任一瞬间均从电源吸取能量，并将电能转化为热能，电阻元件是耗能元件。

瞬时功率实用意义不大，通常电路的功率是指瞬时功率在一个周期的平均值，称为平均功率（也称有功功率），用表示。

4.电感元件伏安关系的相量形式

（1）电感元件的电压与电流相量关系

如图3-37（a）所示的电感元件电路，设，在正弦稳态下伏安关系为：

图3-37　电感元件伏安关系的相量形式

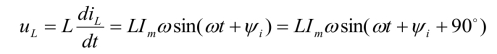
其相量形式为

(www.xing528.com)

式（3-34）称为电感元件伏安关系的相量形式，由此我们可得出：

，电感元件的端电压有效值等于电流有效值、角频率和电感三者之积。

，电感上电压相位超前电流相位90°。

图3-37（b）所示的电路给出了电感元件的端电压、电流相量形式的示意图，图3-37（c）所示的电路给出了电感元件的端电压与电流的相量图。

由式（3-34），得

记，称之为电感元件的感抗，国际单位制（SI）中，其单位为欧姆（Ω）。称为感纳。

感抗时用来表示电感元件对电流阻碍作用的一个物理量。在电压一定的条件下，感抗越大，电路中的电流越小，其值正比与频率。有两种特殊情况如下：

。即电感元件对高频率的电流有极强的抑制作用，在极限情况下，它相当于开路。因此，在电子电路中，常用电感线圈作为高频扼流圈。

。即电感元件对于直流电流相当于短路。

图3-38　感抗随频率变化曲线

图3-39　功率随频率变化曲线

感抗随频率变化的情况如图3-38所示曲线。一般地，电感元件具有通直流隔交流的作用。

必须注意，感抗是电压、电流有效值之比，而不是它们的瞬时值之比。

例3-13一个=10mH的电感元件，其两端电压为，

当电源频率为50HZ与50 kHZ时，求流过电感元件的电流I。

解　当=50HZ时

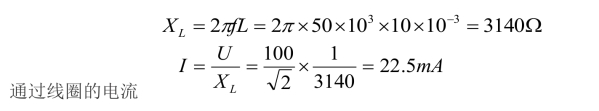
可见，电感线圈能有效阻止高频电流通过。

（2）电感电路的功率

假设电流的初相角，瞬时功率的表达式：

可见p是一个以2的角频率随时间交变的正弦量，其变化曲线如图3-39所示。

在第一和第三个1／4周期内，为正值，这表示电感从电源吸收电能并把它转换为电磁能储存起来。电感相当于负载。在第二和第四周期内，为负值，表明电感将储存的磁场能转换为电能送还给电源，电感起着一个电源的作用。

电感电路的平均功率为：

电感电路的平均功率在一个周期内等于零，故没有能量消耗，也就是说电感从电源吸收的能量全部送回电源。

5.电容元件伏安关系的相量形式

（1）电容电路的电压与电流相位关系

如图3-40（a）所示正弦稳态下的电容元件，设，在正弦稳态下的伏安关系为：

图3-40　电容元件伏安关系的相量形

式（3-35）称为电容元件伏安关系的相量形式。由此我们可得出

，即电容上电流有效值等于电压有效值、角频率、电容量之积；

，即电容上电流相位超前电压相位90°。

如图3-40 （b）所示为电容元件的电压、电流相量形式的示意图，如图3-40（c）所示为电容元件端电压、电流的相量图。

由式（3-36），得

记，称之为电容元件的容抗，国际单位制（SI）中，其单位为Ω，其值与频率成反比；，称之为电容元件的容纳，其单位为S。

对于两种极端的情况，有

①。电容元件对高频率电流有极强的导流作用，在极限情况下，它相当于短路。因此，在电子线路中，常用电容元件作旁路高频电流元件使用。

②。即电容对于直流电流相当于开路。因此，电容元件具有隔直流通交流的作用。

在电子线路中，常用电容元件作隔离直流元件使用。容抗和容纳随频率变化的情况如图所示。必须注意，容抗是电压、电流有效值之比，而不是它们的瞬时值之比。

图3-41　电容随频率变化曲线

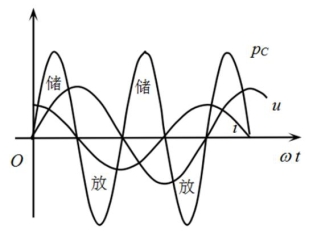
图3-42　功率随频率变化曲线

（2）电容电路的功率

假设电压的初相角，瞬时功率的表达式：

瞬时功率的波形如图3-42所示可知，在第一和第三个1／4周期内，为正值，这表示电容从电源吸收电能并把它转换为电场能储存起来。在第二和第四周期内，为负值，表明电容将储存的电场能转换为电能送还给电源。

电容电路的平均功率在一个周期内等于零，故也没有能量消耗，只与电源进行等量交换。和电感电路相似。