【摘要】：比较等式两边的振幅关系应有或，即电阻元件的电压有效值和电流有效值应符合欧姆定律。图3-29线性非时变电阻的正弦稳态特性2.电容元件根据以上所述不难得出电容元件的正弦电压、电流关系。式中表明，电容电压与电流有效值之间的关系为而电压与电流的相位关系则为。例3-12 设、、串联支路中的电流为，试求的表达式。
在关联参考方向下，线性非时变电阻、电容及电感元件的VCR分别为
在正弦稳态电路中，这些元件的电压、电流都是同频率的正弦波。
1.电阻元件
如图3-29（a）所示，设电阻元件通有正弦电流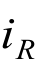
，电阻两端的电压为
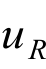，若
，根据欧姆定律得uR=RiR则有
（3-24）式表明，电阻两端的正弦电压和流过的正弦电流频率相同、初相相等，
，波形如图3-29（b）所示。比较等式两边的振幅关系应有
或
，即电阻元件的电压有效值和电流有效值应符合欧姆定律。
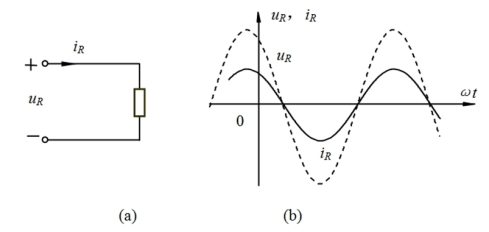
图3-29 线性非时变电阻的正弦稳态特性
2.电容元件
根据以上所述不难得出电容元件的正弦电压、电流关系。若电容两端电压为
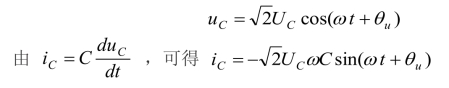
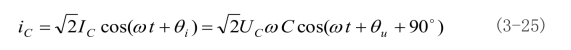
电容电压、电流的波形如图3-30（b）所示。式中表明，电容电压与电流有效值之间的关系为
(https://www.xing528.com)
而电压与电流的相位关系则为
。由此可见，电容电压滞后其电流的相位为
。式中的
具有与电阻相同的量纲。当ω=0时，，此时电容相当于开路。
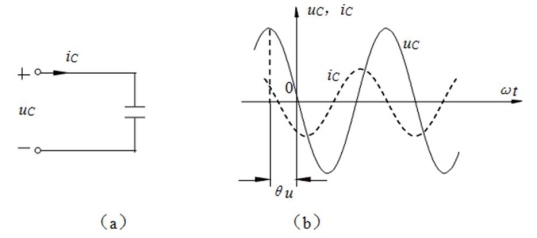
图3-30 线性非时变电容的正弦稳态特性
3.电感元件
对于电感元件来说，根据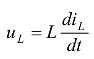
，则有
（3-27）式表明，θu=θi+90°，电感电流iL的相位滞后电感电压的相位为
。电感电流与电压有效值的关系为
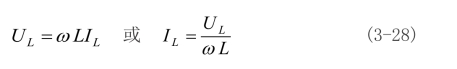
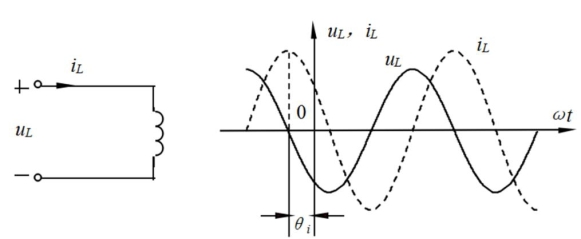
图3-31 线性非时变电感的正弦稳态特性
式（3-28）中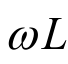
具有与电阻相同的量纲。当
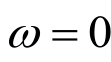时，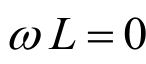
，此时电感相当于短路。
图3-31为电感电压、电流波形图。
例3-12 设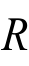
、
、
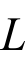串联支路中的电流为
，试求
的表达式。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
