熔态钎料与固体母材的润湿优化

了解钎焊的过程，首先需要了解熔态钎料与母材的润湿过程。现在先从润湿的物理状态开始讨论。

1.2.2.1 液滴在平面固体上的润湿行为

一滴液体在固体表面润湿时如图1-2a所示，液滴与母材之间会出现润湿角θ，如果液滴和固体间仅以色散力相互作用，也就是说，不存在任何物理的互溶、渗透以及任何的化学反应，这时润湿角θ与固体的表面张力F_s（亦即是固体与空气的界面张力），液体的表面张力F_l（亦即是液体与空气的界面张力）和固-液的界面张力F_sl存在以下的关系，称为Young’s平衡式：

F_sl=Fs-F_lcosθ （1-1）或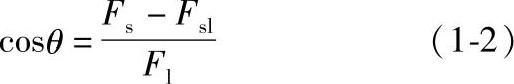

由式1-1可以看出，当润湿角θ为0°时（见图1-2b），cosθ=1，也就是说，完全润湿时，固-液间的界面张力是固、液表面张力之差。

F_sl=Fs-F_l （1-3）

当润湿角为90°时（见图1-2c），cosθ=0，固-液界面张力等于固体的表面张力。

F_sl=F_s （1-4）

当润湿角θ等于180°时（见图1-2d），即完全不润湿的情况下，cosθ=-1，固-液的界面张力是固、液表面张力之和：

F_sl=F_s+F_l （1-5）

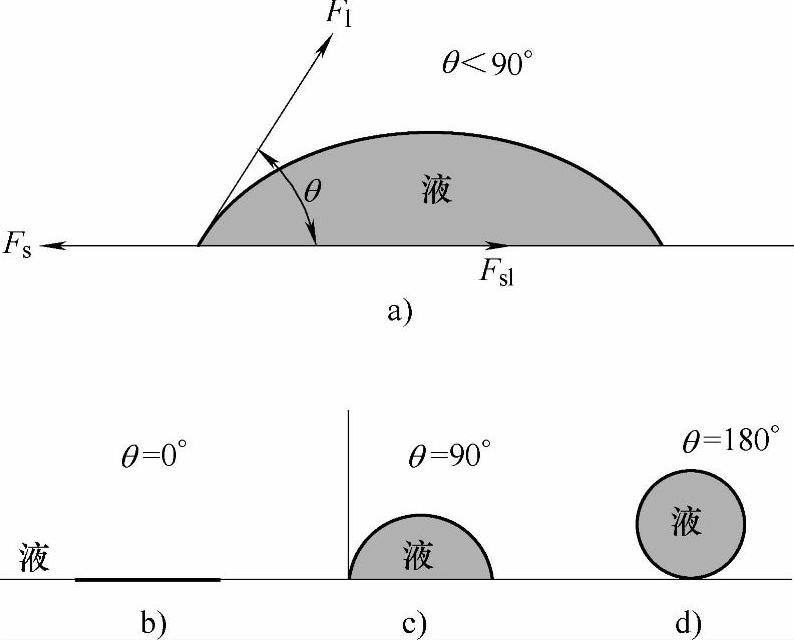
图1-2 液滴在固体表面的润湿 Fig.1-2 A liquid drop wetting on the solid surface

从这里得出的结论是：界面张力F_sl和润湿角θ呈正相关，也即润湿角θ越小，界面张力F_sl也越小。或者换句话说，要想液-固润湿得好，就要降低固-液间的界面张力。

1.2.2.2 液体在狭窄缝隙中的润湿行为—毛细现象

将一根直径为λ的毛细管插入液体内（见图1-3），液体和管壁就会产生一个润湿角θ。在润湿角θ和液体表面张力F_l（液体和空气之间的界面张力）综合力的作用下，管内的液面会发生变化。

当θ<90°时，管中液面会上升，如水在玻璃管中就是这样（见图1-3a）。这个过程是这样的：由于液体润湿了管壁产生了润湿角θ，管内的液面就会出现深的弯月形曲面，但这时液体的表面张力则力图将弯月面拉平，这样就使得液面微有上升。但是液体又向上润湿一个新的θ角，表面张力再度拉平液面。如此反复，液面就不断爬升。爬升的过程中却同时受到液柱重力的反制。当这个润湿角和液体表面张力综合形成的爬升力和液柱所受重力平衡时，液柱就会稳定在一个h的高度上。下面等式左侧是爬升力，右侧是液柱所受的重力：

或

式中 F_l——液体表面张力；

θ——润湿角；

g——重力加速度；(www.xing528.com)

ρ——液体的密度；

λ——毛细管的直径；

h——液柱高度。

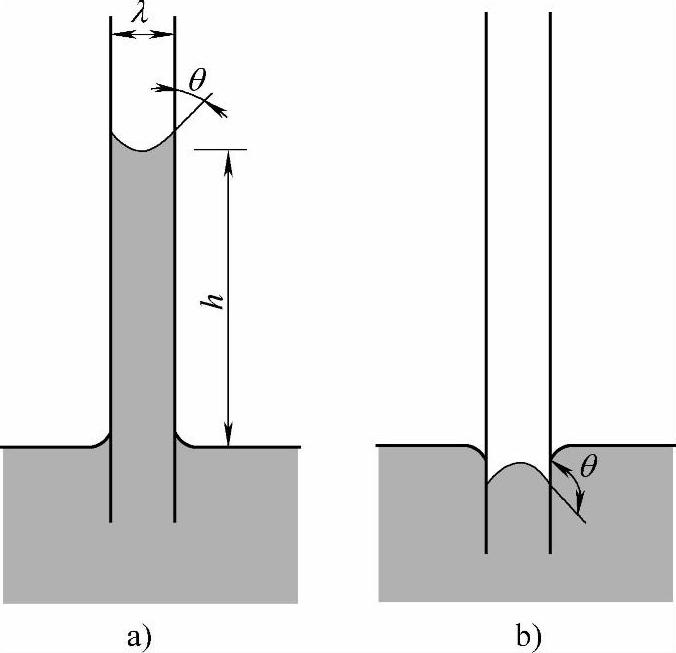
图1-3 毛细管中液面的变化 Fig.1-3 Variation of the liquid surface in capillary tubes

对于固定的一种液体，分母中gρ乘积的值是固定的。可以看出，毛细管中液面爬升的高度和管径λ成反比，和液体表面张力F_l（液体和空气之间的界面张力）成正比，还和润湿角θ成反比（这是因为θ在0°→90°时，cosθ是从1减少到0）。也就是说，管径越小，液体的润湿角越小，液体的表面张力（即液态钎料与空气的界面张力）越大，越有利于液柱的爬升。

当θ=90°时，cosθ=0，h=0，毛细管内外液面持平，没有爬升。

但是当θ>90°时，毛细管内液柱不升反降（见图1-3b），因为在90°→180°时（见图1-3b），cosθ值是0→-1，h值成为负值，所以这时液面会出现下降，θ值越大，液面下降得越多。可以见到的实例是玻璃毛细管中的水银。

在实际的钎焊过程中，情况有很大的不同，遇到的不是毛细管而是两片母材夹成的大面积间隙，而且常常间隙是水平放置的，较少像上述毛细管的垂直放置（见图1-4）。

图1-4 液体在平面间隙中的润湿 Fig.1-4 Wetting of the liquid in a gap between two plates

可以看出，在考察钎焊过程的实际时，情况要复杂得多，很难定量地描述液态钎料在间隙中的流布。这时不妨将上述液柱的爬升力，定性的看成是液态钎料在间隙中向前流动的驱动力，那么就同样也可以得出：钎焊时母材间隙越小，液态钎料润湿母材的润湿角越小，液态钎料的表面张力（即液态钎料与空气的界面张力）越大，越有利于液态钎料在母材间隙中的向前流布。

在实际钎焊过程中，熔态钎料在大面积母材狭缝中流动的行为非常复杂，难于描述。钱乙余等利用X射线荧光增强仪摄制了液态钎料在平行的狭缝中流动的动态模拟。结果表明，这是一个无规则的紊流过程，伴随着熔态钎料的多头前进、包抄、围困和产生夹芯，看来在空气中进行大面积钎焊，钎缝中存在缺陷是难以避免的。为了解决这一难题，提出了不等间隙的钎焊流程，得以有效排除夹芯的产生。

固体的表面张力实际上是固-气的界面张力F_sg。在大气中，固体本身有很多因素都影响自身的表面张力，例如成分、组成、晶格缺陷、表面分凝和力学应变等等。其中表面分凝影响最大。固体的表面张力难以理论界定、测量和控制。但是因为固体的表面张力实际上是固-气的界面张力F_sg，改变固体界面上的气氛，显然会对F_sg能够产生影响。在真空和一些还原性气氛，如氢气中，F_sg会有明显的下降。

液体的表面张力的物理意义和量值明确，是指增加单位表面积液体时自由能的增值。液体的表面张力是易于测定的。其法定单位为mN/m（毫牛/米），以前常用dyn/cm（达因/厘米）。液体金属的表面张力常在200～2500mN/m之间。液体的表面张力随温度的升高而线性下降，因此升高温度有利于润湿。图1-5所示为不同熔态金属的表面张力与温度变化的关系。

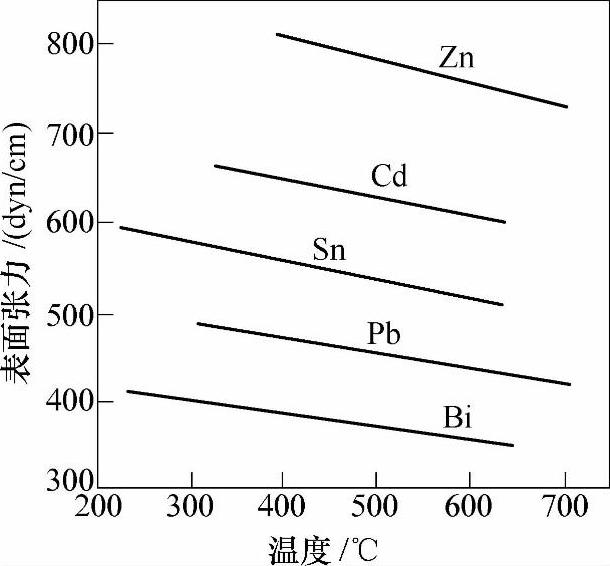
图1-5 不同熔态金属的表面张力与温度变化的关系 Fig.1-5 Temperature dependence of surface tension for different molten metals 注：1dyn/cm=10^-2mN/cm

以上的叙述局限于液-固金属间仅以色散力相互作用的情况，其间既无化学反应发生，也无相互溶解和原子渗透等物理反应发生。但实际上影响液态金属（钎料）和固体金属（母材）之间润湿行为的更大因素是它们之间的相关系（phase rela-tion）。这已超出式（1-1）讨论的范围。

熔态钎料与母材间如有一定的反应性，通常能够很好地润湿，反之则较难润湿。所谓的反应性，包括液态钎料和母材间的互溶或金属间化合物的生成。然而影响润湿最主要的因素是互溶度。例如液态Zn和固体的Al在500℃有近30%的溶解度，它们润湿得很好。液态Pb和固态Al在500℃时几乎完全没有互溶度，它们极难润湿。这些关系可以从Al-Zn和Al-Pb的相图上看出来。类似的情况如液态Ag在1200℃时与Fe的互溶度几乎为零，而Cu在同样的温度下能溶Fe近5%，实际的表现是前者难润湿而后者则较易。但在这种情况下，如果不用纯Ag，而是在Ag中加入一定比例的、能与Fe互溶的Cu或Zn形成合金，就能大大改善这种银合金与母材Fe间的润湿性。特别是加入Pd，由于它和Fe、Co、Ni、Cu、Ag、Au等金属不但在液相，就是在固相也有完全的互溶度，增加润湿性最有效，由此导致发展许多含Pd的钎料。因此对合金钎料，通常其中各主要成分与母材的相关系，决定了合金钎料与母材润湿的综合效果。