新型自动怠速的数学模型优化方案

图7-32所示为新型自动怠速系统的结构简图，通过建立系统的数学模型来分析新型自动怠速系统的控制特性。先作出如下假设。

1）忽略电磁换向阀对执行器速度特性的影响。

2）这里只考虑液压缸伸出的运动，忽略由于液压缸的活塞运动对液压缸无杆腔、液压蓄能器和液压泵之间压力容腔体积的影响。

3）液压缸和液压泵均无弹性负载。

4）系统安全阀未溢流，补油单向阀未打开。

5）液压泵的进口压力为零。

（1）变频器-动力电动机环节的电磁力矩方程

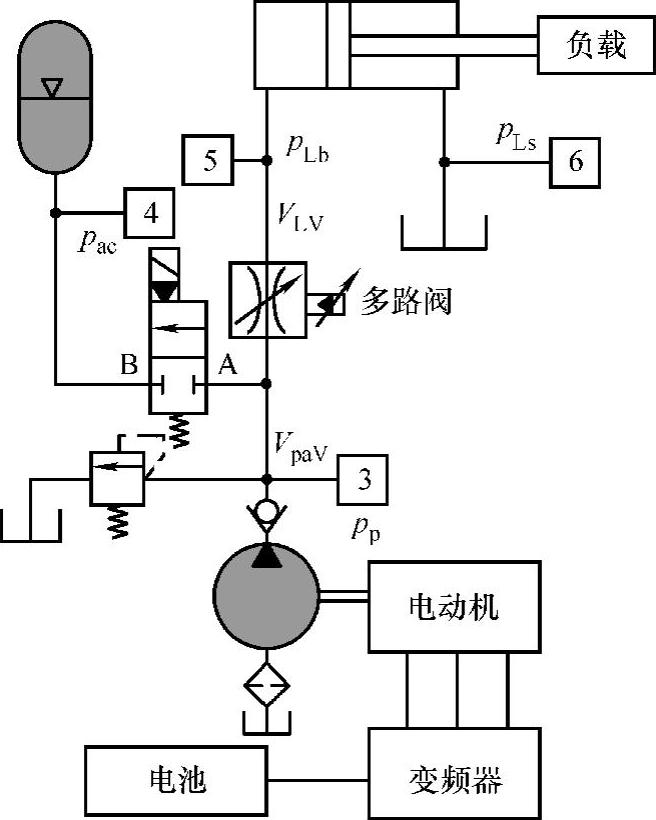
图7-32 新型自动怠速系统的结构简图

采用异步电动机作为动力电机，由于异步电动机的电磁瞬变过程要比机电瞬变过程快得多，而且考虑到变转速容积调速系统的动态过程中，变频器-动力电动机的电磁场产生目标电磁转矩的时间远小于液压泵-动力电动机的机械响应时间，因此变频器和动力电动机可以假设为一个比例环节：

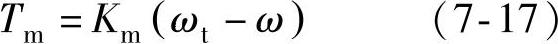
式中，T_m为动力电动机的电磁力矩（N·m）；K_m为动力电动机转矩和转速差的比例系数；ω_t为动力电动机目标角速度（rad/s）；ω为动力电动机的角速度（rad/s）。

（2）液压泵输出流量方程

式中，q_p为液压泵的排量（m³/rad）；C_ip和C_ep分别为液压泵的内泄漏和外泄漏系数[m³/（Pa·s）]；C_tp为泵的总泄漏系数[m³/（Pa·s）]，C_tp=C_ip+C_ep；p_p为泵的出口压力（Pa）。

（3）动力电动机-液压泵的负载力矩方程

如上述假设，忽略弹性负载与外干扰力矩，则动力电动机-液压泵的负载转矩方程为：

电动机-泵的转矩平衡方程为：

式中，T_L为液压泵的负载力矩（N·m）；J为液压泵、电动机及联轴器的总转动惯量（kg·m²）。b_m为粘性阻尼系数（N·m·s/rad）。

（4）比例方向多路阀的流量方程

式中，q_C为流过比例方向多路阀的流量（m³/s）；K_q为比例方向多路阀的流量增益（m²/s）；K_C为比例方向多路阀的流量压力系数[m³/（Pa·s）]；x_v为比例方向多路阀阀口开度位移（m）；p_Lb为液压缸无杆腔压力（Pa）。

（5）液压蓄能器的流量方程

(www.xing528.com)

式中，q_ac为液压蓄能器的输出流量（m³/s）；p₀和p_ac分别为液压蓄能器的充气压力和工作压力（Pa）；V₀为液压蓄能器的额定体积（m³）。

（6）油液的连续性方程

液压缸的连续性方程为：

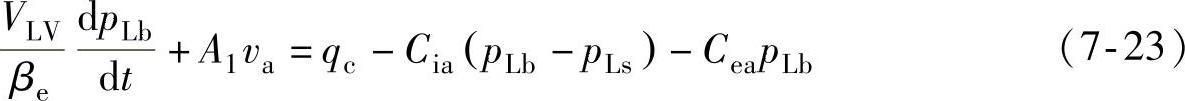
液压泵的连续性方程为：

式中，β_e为有效体积模量（Pa）；V_paV为泵、液压蓄能器和比例方向多路阀之间的体积（m³）；V_LV为液压缸无杆腔和比例方向多路阀之间的体积（m³）；A₁为液压缸无杆腔的有效作用面积（m²）；v_a为液压缸的运行速度（m/s）；C_ia和C_ea分别为液压缸的内泄漏和外泄漏系数[m³/（Pa·s）]，两者之和为液压缸的总泄漏系数C_ta[m³/（Pa·s）]，C_ta=C_ia+C_ea。

当液压缸作伸出运动时，有杆腔的压力为零，即p_Ls=0。因此，方程（7-24）可以写成：

（7）液压缸的力平衡方程

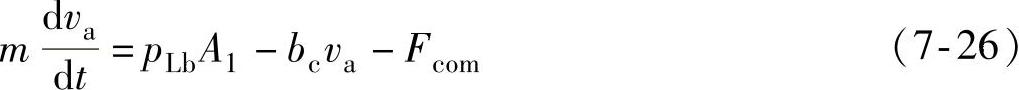
式中，m为液压缸活塞及负载折算到活塞杆上的总质量（kg）；b_c为液压缸活塞及负载的粘性阻尼[N/（m/s）]；F_com为液压缸伸出时受到的库伦摩擦阻力（N）。

根据上述方程，由拉普拉斯变换并整理可得：

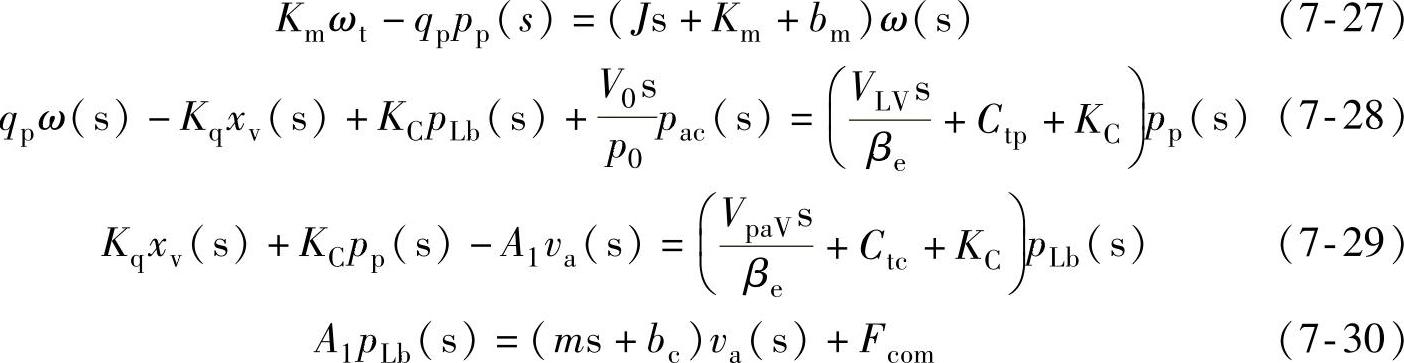
最后整理化简得到：

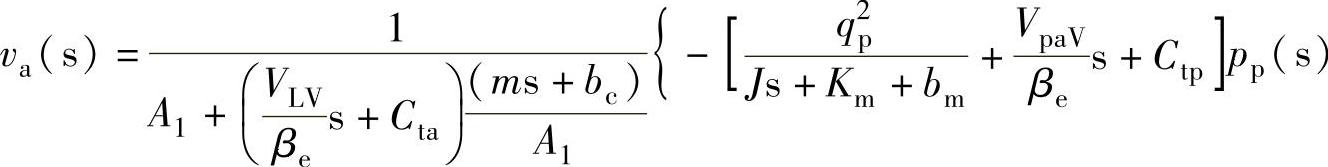
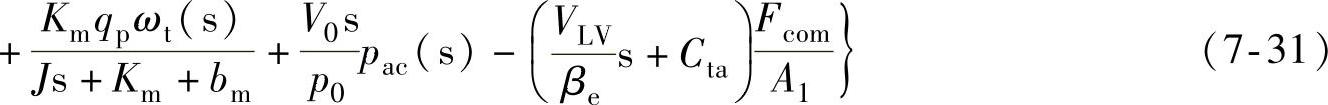
在分析液压缸速度特性时，暂时不考虑动力电动机特性和库伦摩擦阻力（看作常数）对液压缸速度的影响，同时忽略液压泵和液压缸的泄漏影响。因此，式（7-31）可以化简为：

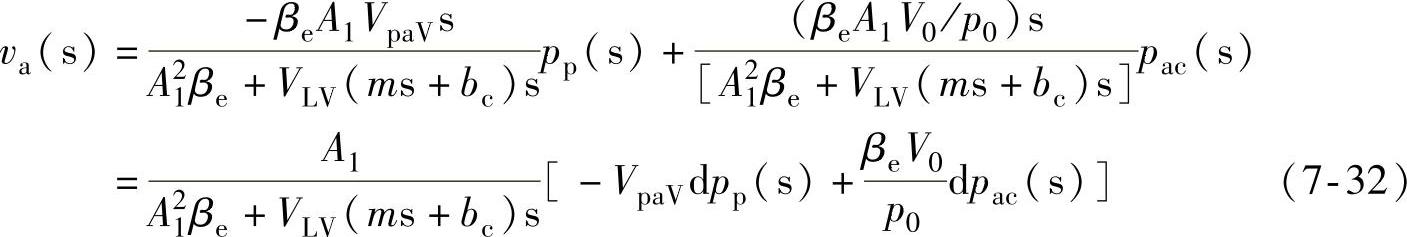
式中，dp_p和dp_ac分别为液压泵和液压蓄能器的压力变化率。

如果不考虑液压蓄能器对液压缸速度的影响，则可以得到传统自动怠速系统的液压缸速度控制方程：

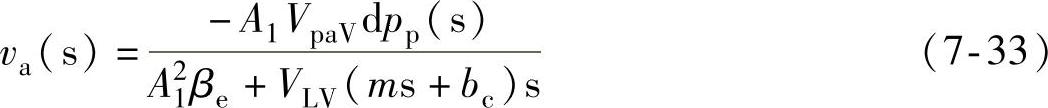
因此可以得到传统自动怠速系统的液压固有频率和阻尼比为：

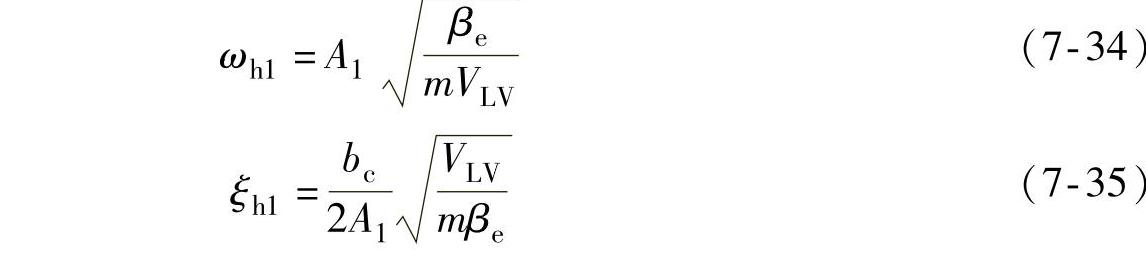
因此从上面的公式可以看出，两种自动怠速系统的区别在于，有液压蓄能器的自动怠速系统同时还受到液压蓄能器压力变化率的影响。从上述传递函数可以看出，液压缸的速度特性同时受液压蓄能器的额定体积V₀和充气压力p₀，以及执行器与比例方向阀之间的体积V_LV、液压泵、液压蓄能器和比例方向多路阀之间的体积V_paV影响。下面将对这些影响因素进行仿真研究。