系统建模与控制特性分析

为了研究方便，首先将图5-1简化成图5-2，在此系统中，通过调节液压马达的转速来控制液压马达的流量，在执行元件的回油腔形成背压，从而控制液压执行元件的运行速度。在建模分析时，可以对系统进行以下假设。

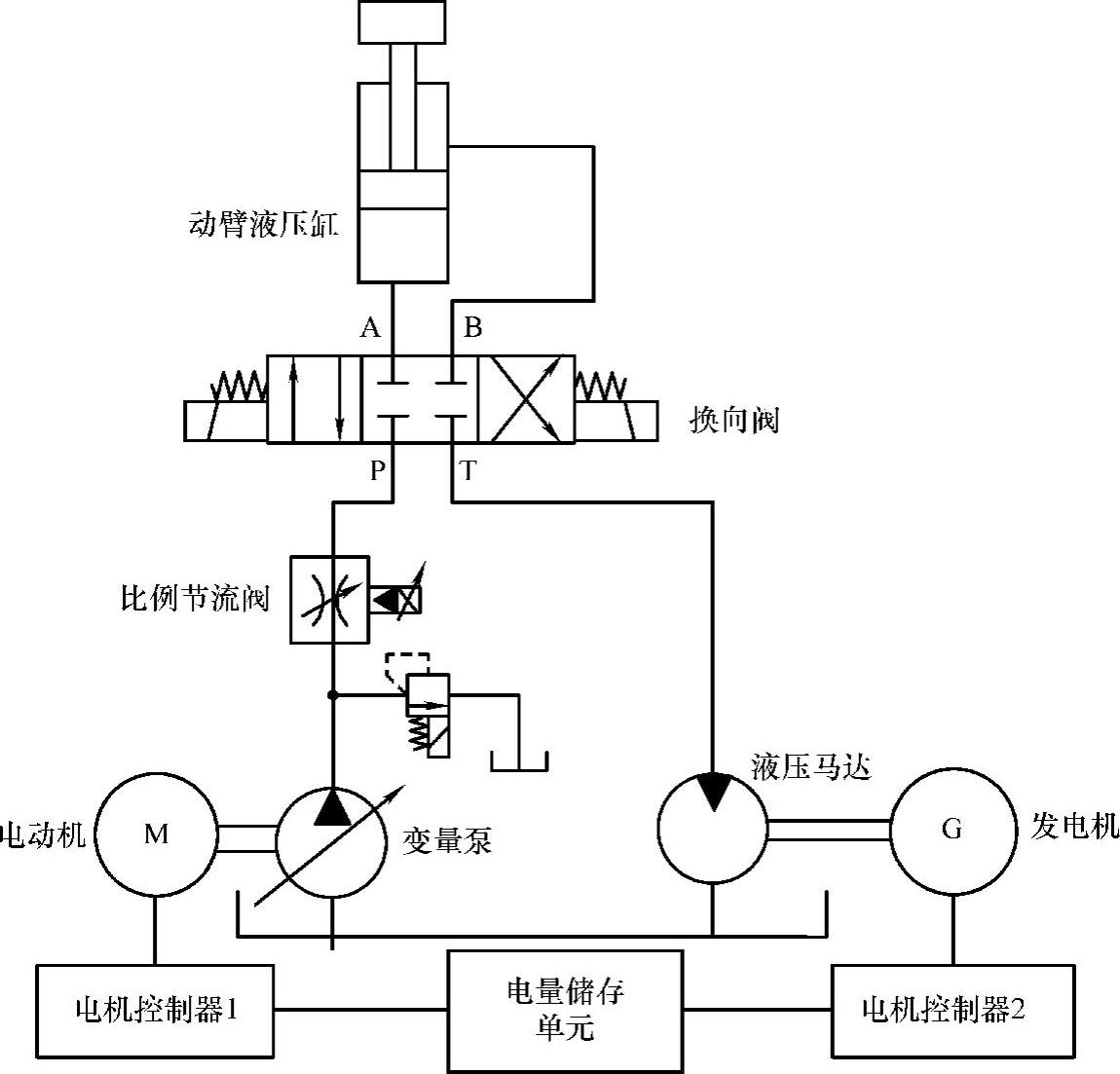
图5-1 液压马达-发电机能量回收系统简化示意图

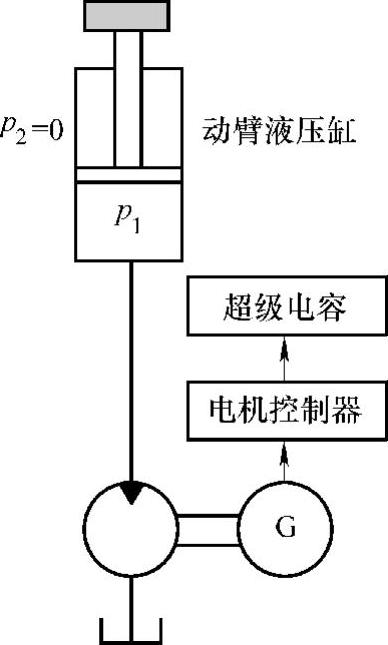
图5-2 液压挖掘机基本能量回收系统简化原理图

1）由于液压马达主要是对执行机构下放时的重力势能进行回收，因此仅以液压缸回缩时作为研究对象，不考虑其外伸过程。

2）忽略了换向阀对动臂速度特性的影响。

3）液压马达和发电机同轴相连。

4）动臂下放时，忽略由于动臂液压缸的活塞运动对动臂液压缸无杆腔和液压马达之间压力容腔体积的影响。

5）动臂液压缸和液压马达均无弹性负载。

6）系统安全阀未溢流，补油单向阀未打开。

7）液压马达回油压力为零。

8）每个腔室内的压力是均匀相等的，液体密度为常数。

9）液压马达排量恒定。

1.动臂速度控制数学模型

（1）基本电气式能量回收系统数学模型的建立

1）液压马达流量方程

q_m=ωV_m+C_imp₁+C_emp₁ （5-1）

式中 C_im——液压马达内泄漏系数（m³/Pa·s）；

C_em——液压马达外泄漏系数（m³/Pa·s）；

ω——发电机和液压马达的角速度（rad/s）；

V_m——液压马达的排量（m³/rad）；

p₁——液压缸无杆腔和液压马达之间的容腔压力（Pa）。

2）油液的连续性方程

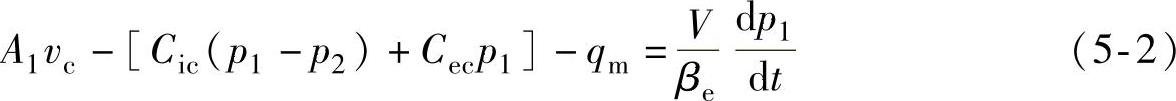
式中 C_ic——液压缸内泄漏系数（m³/Pa·s）；

C_ec——液压缸外泄漏系数（m³/Pa·s）；

V——液压缸无杆腔与液压马达之间的容腔容积（m³）；

β_e——有效体积弹性模量（Pa）；

A₁——液压缸无杆腔的有效面积（m²）；

v_c——活塞运动速度（m/s），取向下为正。

由于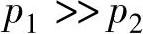，所以p₁-p₂≈p₁。

令系统的总泄漏系数为

C_t=C_ic+C_im+C_ec+C_em （5-3）

则式（5-1）和式（5-3）代入式（5-2）后，可简化为

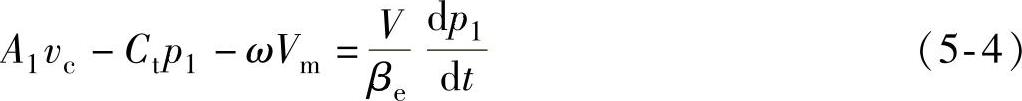
3）液压缸的力平衡方程

忽略弹性负载与外扰力后，液压缸与负载的力平衡方程为

式中 m——液压缸活塞及负载折算到活塞杆上的总质量（kg）；

b_c——液压缸活塞及负载的粘性阻尼（N·s/m）；

p₂——液压缸有杆腔内的压力（Pa）；

A₂——液压缸有杆腔内的有效面积（m²）。

动臂下放时，对于液压缸有杆腔的压力油来说，液压缸活塞及负载折算到活塞杆上的总质量为一个负负载，其有杆腔的压力很小，为了只研究重力势能的回收效果，排除有杆腔的压力对能量回收的影响，假设当液压缸靠重力快速下落时其有杆腔的压力很低，即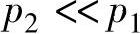，式（5-5）可简化为：(www.xing528.com)

4）液压马达的转矩平衡方程

忽略弹性负载与外干扰转矩，液压马达与负载的转矩平衡方程为

式中 T_g——用作发电机的发电转矩（N·m）（电动为正，发电为负）；

J——液压马达-发电机等效转动惯量（kg·m²）；

b_m——液压马达回转的粘性阻尼（N·m·s）。

5）发电机的物理方程

永磁同步发电机一般采用矢量控制，即把交流电机模拟成直流电机控制，这里仅考虑矢量变频控制中的转速环。对于矢量控制变频电机，由于电机控制器及电机的电磁产生目标电磁转矩的时间远小于液压马达-发电机的机械响应时间，因此电机控制器和发电机可以假设为一个比例环节：

T_g=Kg（ω_t-ω） （5-8）

式中 K_g——发电机转矩和转速差的比例系数N·m/（rad/s）；

ω_t——发电机目标角速度（rad/s）。

对式（5-4）、式（5-6）、式（5-8）进行拉氏变换得：

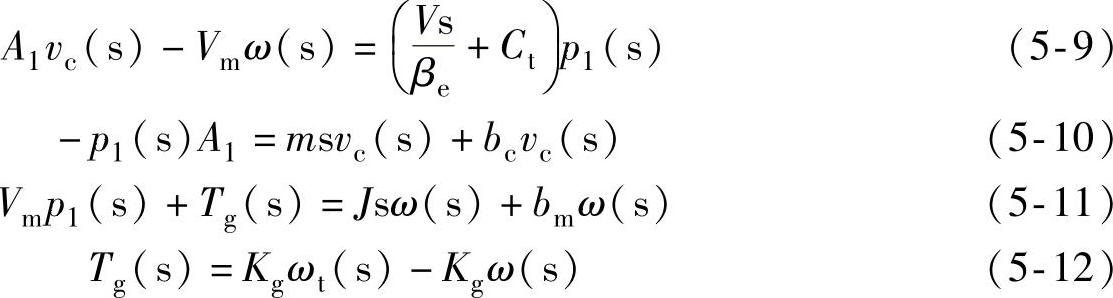
由式（5-9）～式（5-12）整理得

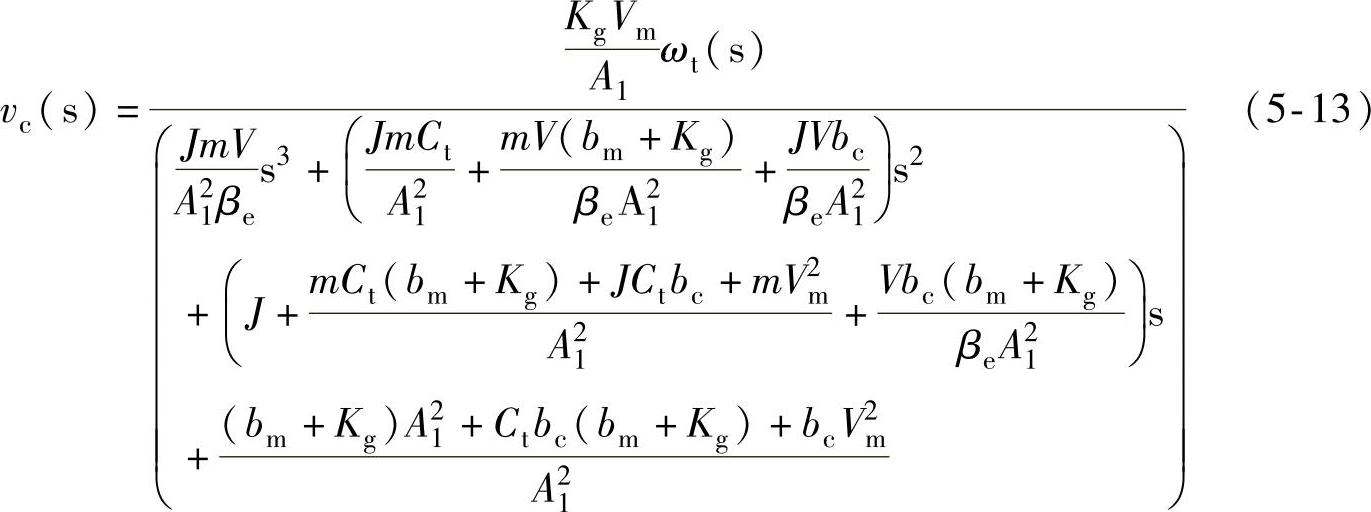
由于液压挖掘机的惯性负载相对于液压缸和液压马达来说比较大，为了便于分析系统的模型，这里忽略系统中液压缸和液压马达的粘性阻尼，即b_c=b_m=0，则式（5-13）可以进一步简化成下式。

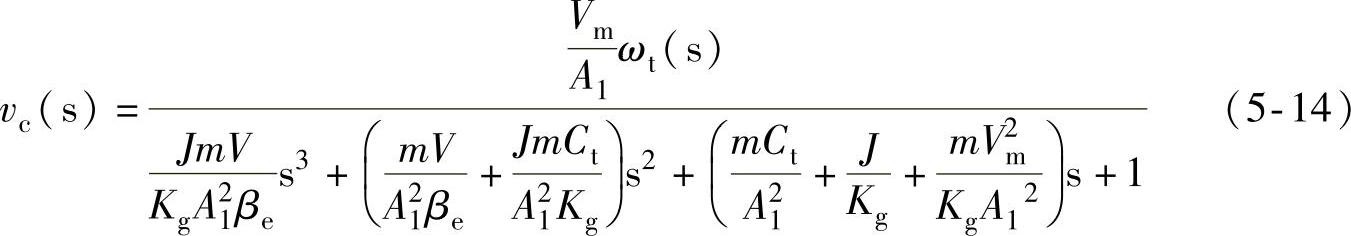
分母中的第一项和第二项为

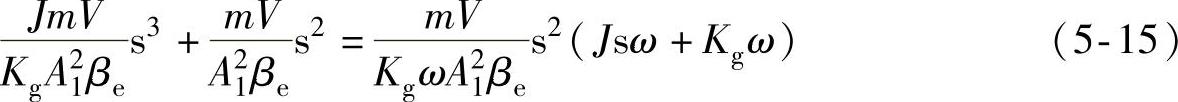
式（5-15）中右侧括号中第1项是转速对液压马达惯性转矩的影响，第2项是电动机由于转速变化而引起的转矩变化。一般液压马达和发电机的等效转动惯量很小，而发电机的刚性比较大，所以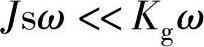，则式（5-15）变为

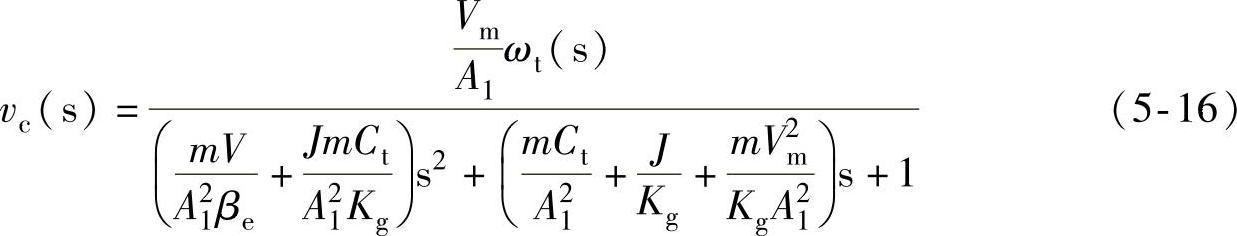
由此可以得到液压挖掘机基本能量回收系统的液压固有频率和阻尼比：

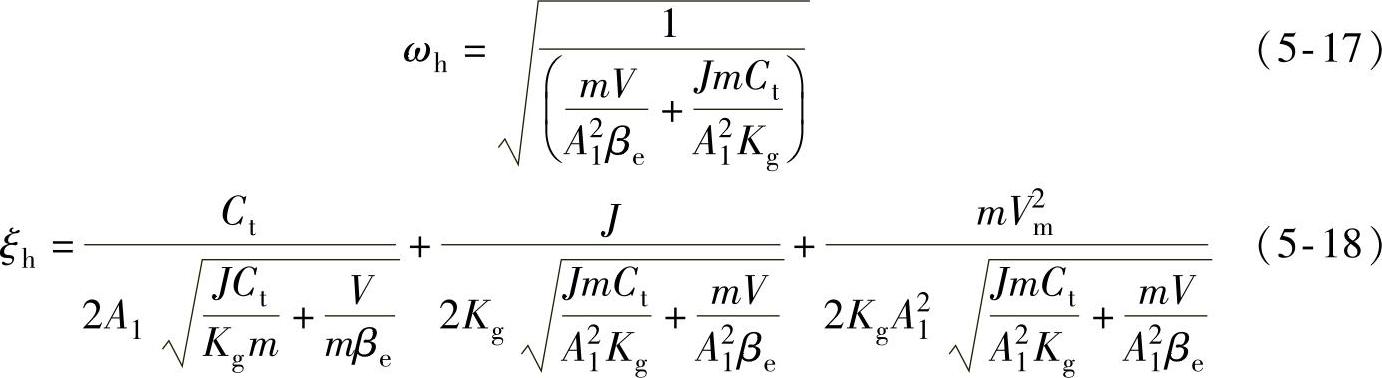
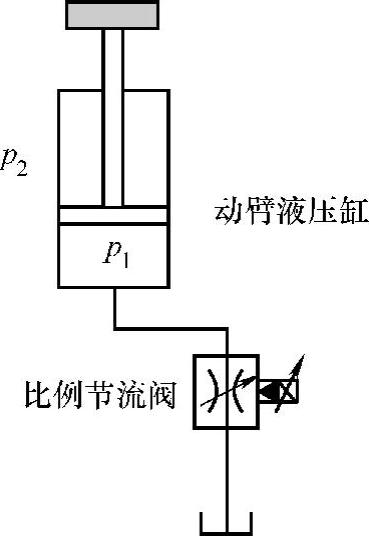
图5-3 液压挖掘机传统节流控制系统简化原理图

（2）传统回油节流控制系统数学模型的建立

为了对比研究基本能量回收系统的控制性能，建立传统节流调速系统的数学模型。由于动臂下放时负负载的存在使得动臂液压缸的有杆腔压力很小，使得动臂有杆腔压力对动臂速度控制的影响很小，因此可以把动臂下放过程的速度控制系统简化成图5-3所示的系统。

1）比例节流阀的流量方程

q_J=K_qx_v+K_Cp₁ （5-19）

式中 K_q——比例节流阀的流量增益（m²/s）；

K_C——比例节流阀的流量压力系数（m³/Pa·s）；

x_v——比例节流阀阀芯开度（m）。

2）油液的连续性方程

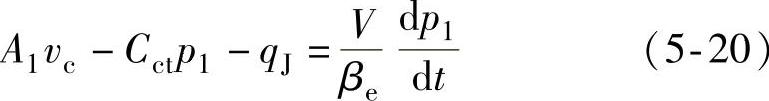
3）液压缸的力平衡方程同式（5-6）。

对式（5-19）、式（5-20）、式（5-6）进行拉氏变换后整理得到

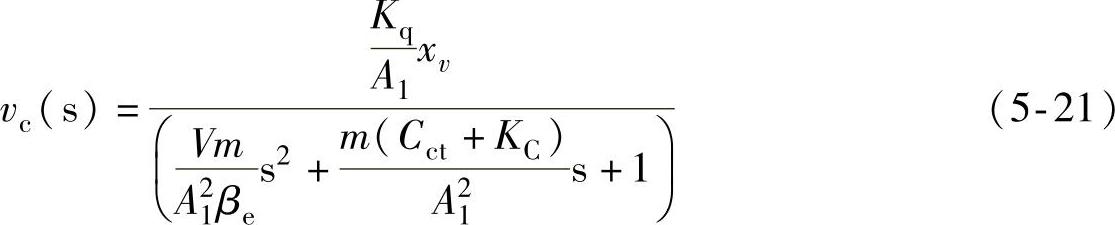
由此可到传统节流调速系统的液压固有频率和阻尼比

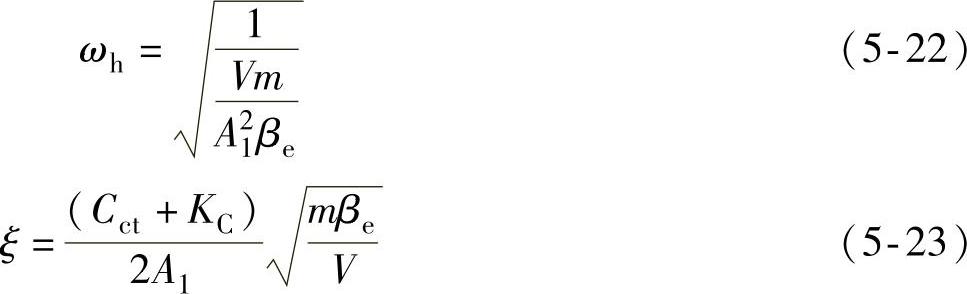
2.基本能量回收系统的控制特性分析

由式（5-17）和式（5-22）相比可以看出，考虑发电机特性后，系统的液压固有频率变小了，使得系统的动态响应进一步减小，同时液压马达-发电机的转动惯量J越大和发电机转矩和转速差的比例系数K_g越小时，其固有频率越小。由式（5-18）可以看出，当液压马达-发电机等效转动惯量J较小和发电机转矩和转速差比例系数K_g较大时，发电机特性对系统固有频率的影响较小，但减少液压马达发电机等效转动惯量J和增大发电机比例系数K_g会使其阻尼比变小，导致系统的稳定性变差。因此，采用电气式能量回收系统后，发电机转矩和转速差比例系数K_g和液压马达-发电机等效转动惯量J是影响系统固有频率和稳定性的主要因素。

从式（5-18）可以看出，适当增大液压缸活塞面积A₁、提高油液的有效体积弹性模量β_e等可以较小程度改善其控制性能，但改变的余地不大。减小压缩容积V同样也可以提高系统的动态响应，由于系统管道的直径由系统的压力和流量特性决定，因此减少压缩容腔体积的主要方法是，减少液压马达和动臂液压缸无杆腔之间的管道长度。