基于多目标蚁群算法的优化方案设计

为消除多目标及各类约束导致的大量任务间冲突，获得问题的Pareto解集，采用多目标蚁群算法优化网络中传输节点-控制器选择。针对蚁群算法在应用过程中存在收敛慢、容易出现停滞现象、运算时间长等不足，本节引入自适应状态转移和基于拥挤距离的精英选择策略，算法具体流程如图8.6所示。

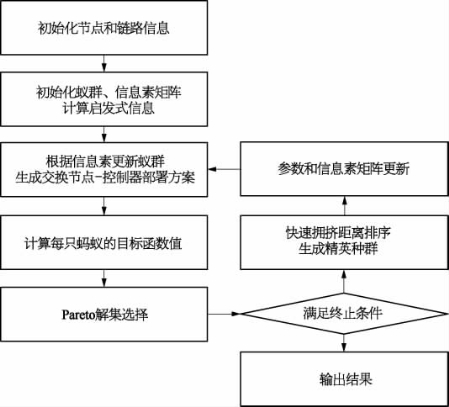
图8.6　算法流程

1）问题编码

算法中每一个蚂蚁都表示为控制器部署问题的解，即一种可能的控制器分配方案，解集长度为传输节点个数n，每一个解为

解中的第i个位置对应于第i个节点所接入的控制器，每个节点的控制器选择xi构成控制器分配方案X，并针对X依次进行目标函数F（X）=｛f1，f2，f3｝的计算，从而评价该方案效果的优劣。对于多目标控制器部署问题，平均传播时延、全网中断概率和资源负载失衡度3个目标值在一定程度上存在矛盾，难以得到3个目标值均最优的控制器部署方案；因此，对于方案X1和X2，若满足F（X1）≤F（X2），且∃i∈｛1，2，3｝，使fi（X1）＜fi（X2），则称为F（X1）支配F（X2），记为F（X1）＞F（X2）。对于方案X*和∀k，均不存在F（Xk）＞F（X*），则称X*为非劣（Pareto）解。对于多目标控制器部署问题，关键在于获得其Pareto解集。

2）状态转移概率

在可行解的构造过程中，设迭代次数为t，每只蚂蚁根据第t-1次迭代的信息来进行本次控制器选择。对于每只蚂蚁中的每个节点，系统产生一个随机数rq，设定一个启发选择比例q（有q∈［0，1］），根据随机数rq与q的关系，每个传输节点对控制器的选择有两种方式：

式中，τi，j（t）为第t代信息素浓度，ηi，j（t）为启发式信息，α和β为对应项的重要程度，Vc为节点i可选择的控制器候选集。

若随机数rq小于q，则选择与该节点间具有最大信息素的控制器作为节点接入的控制器。

若随机数rq大于q，则按照轮盘赌方法依下式状态转移概率选择节点接入的控制器。

式中，ηi，j（t）由节点i和j之间最短路径连通率和最短路径时延综合确定，为了提高网络鲁棒性，应优先选择最短路径连通率高且时延较低的控制器节点进行接入，故定义启发式信息为

(www.xing528.com)

式中，γ为调节最短路径连通率和时延的权重系数。

本算法中采用自适应变化的启发选择比例q，在迭代初始阶段，为加快算法收敛速度，式（8.37）中q取较大值；在迭代搜索后期，为增加种群多样性，q取较小值。

式中，Gmax为最大迭代次数，Gcurrent为当前迭代次数，qmax和qmin分别为启发选择比例q的上下限。

3）快速拥挤距离排序

拥挤距离是计算一个解周围其他解的密集程度的评价指标，传统拥挤距离计算方法需要计算解集中所有个体的距离，为了降低计算量，提高算法效率，本节采用一种快速拥挤距离计算方法。对于每一个目标函数，首先根据目标值的大小对Pareto解集Fi中的解进行排序，对于每个解i，计算由解i+1和i-1构成的立方体的平均边长，并将其作为解i的拥挤距离idistance。边界解（其某个目标函数值最大或最小）的拥挤距离为无穷大。拥挤距离idistance的计算方法为

式中，m代表目标函数的个数，fK代表第K个目标函数，和为第K个目标函数的最大值和最小值，拥挤距离越大，则说明解i周围的点越稀疏。

在多目标蚁群算法寻优过程中，Pareto解集内的点均为潜在可行解，设置外部解集A保存已找到的最优解集，A中元素随搜索进行而逐渐增多，其前沿逼近真实的Pareto前沿。为了避免算法向Pareto解密集区域靠近而偏离真实Pareto前沿，将拥挤距离最大的前Nep个解作为精英解集，只对位于精英解集A中的解路径上的信息素进行加强，其信息素浓度随迭代次数的增加而减少。

4）信息素更新策略

在多目标蚁群算法寻优过程中，若某个蚂蚁属于精英解集，则说明该解是不可支配的，该蚂蚁优于不属于精英解集的其他蚂蚁，应该对位于精英解集中的解路径上的信息素进行加强，以便吸引更多蚂蚁。因此，信息素的更新表达式为

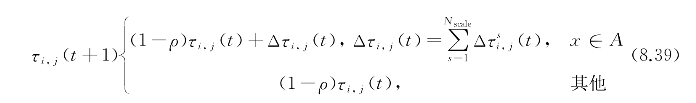
式中，ρ∈［0，1］为信息素挥发系数，Nscale为蚂蚁个数，s为精英个体，Δτi，j（t）为传输节点i与控制器j之间的信息素增量，算法中仅对每一代精英解集中个体路径上的信息素进行加强，采用基于全局信息的Ant cycle模型，即：

式中，Q为信息素增强系数，每一代精英解集中解路径上的信息素具有上下限τmin和τmax。