控制器部署算法的设计与优化

在航空信息网络中存在着功能各异的飞机节点，参考文献［15］，假定在执行某作战任务过程中其网络拓扑保持相对稳定，随着作战任务变化，网络拓扑也相应改变，本节在此基础上对航空信息网络进行进一步集群域划分。

1）航空集群域划分算法

k-means是一种简单高效、快速实现的基于划分原理的聚类算法，其将数据集U=｛x1，x2，…，xn｝按照某种准则划分为若干个子集，其中k为聚类数目，且聚类满足以下约束：

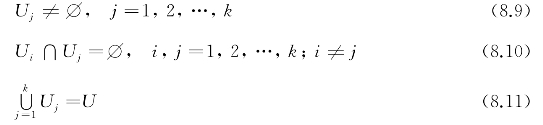
图8.2为传统k-means算法流程，其中输入为数据集U和聚类个数k，输出为聚类划分结果，算法结束的条件为聚类中心不再发生变化或变化范围在规定的阈值内。由于k-means算法是随机选择初始聚类中心的，聚类结果会随初始聚心的改变而改变，因而引入聚类质量评估函数作为聚类效果的评价准则，其中对聚类质量评估函数定义为

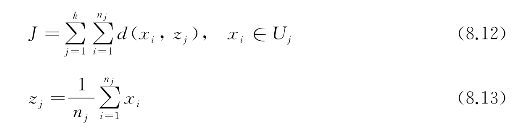
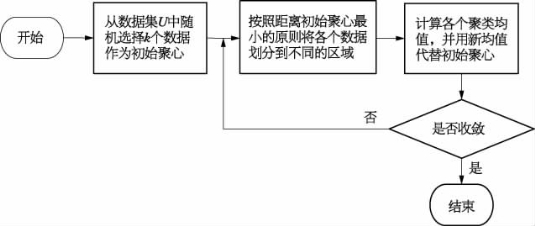
图8.2　传统k-means算法流程

式（8.12）表示各聚类的内距离和，J值越小则代表聚类的效果越优；式（8.13）表示集群域j的聚心。

传统k-means聚类算法是一种贪婪算法，容易陷入局部最优，并且该算法选择的初始聚心极有可能偏离数据密集区，若初始聚心位于孤点或者偏远点，则会导致划分的集群域性能差。针对该问题本节参考文献［16，17］中提出的离群因子对k-means算法初始聚心位置随机这一缺点作些改进，得出一种基于离散因子（discrete factor，DF）的改进kmeans算法，具体如下：

定义1　数据x的第k距离（k-distance）

x的第k距离k-dis（x）指在数据集合U中存在数据o，数据o与数据x之间的距离记为d（o，x），当满足下述条件时，x的第k距离k-dis（x）等于d（o，x）：

（1）数据集U中至少存在k个数据o′∈D＼｛x｝满足d（x，o′）≤d（x，o）。

（2）数据集U中至多存在k-1个数据o′∈D＼｛x｝满足d（x，o′）＜d（x，o）。

定义2　数据x的第k距离邻域

数据x的第k距离邻域指不超过数据x的第k距离内所有数据的集合：

若该集合较大，则说明数据x的第k距离邻域较大，表明数据偏离程度较大，反之偏离程度较小。

定义3　数据x的离散因子

数据x的离散因子指在x的第k距离范围内，集合U中数据的平均分布密度大小，DFk（x）值越大，则x越可能成为离群点，其计算公式为

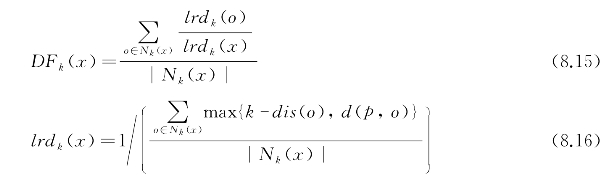(www.xing528.com)

算法1为基于离散因子的改进k-means算法，算法通过计算集合U中各数据的离散因子值，找出离散因子值较小的节点作为候选初始聚心集合，在该集合中通过计算距离进而得出最终的聚心位置，具体如下：

续表

根据上述算法可得到最终的聚心分布结果，相比于传统k-means算法，该算法有效地避免了聚心位于孤点或偏远点，使得聚心分布更加合理。上述算法在构造集群域时主要以节点的分布特点为主，而在实际部署过程中由于LC存在处理能力受限等问题，易造成某LC负载过载或欠载，从而引起数据拥塞或不能充分利用资源等问题，因而在此基础上加入LC负载受限这一约束条件对集群域划分结果进行优化调整。引入负载均衡指数B对各集群域间的负载是否均衡进行计算判断：

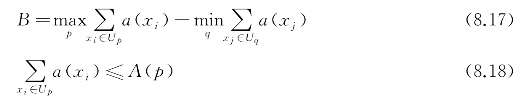
式中，a（xi）表示节点xi向其集群域内的LC提交的数据请求信息，且集群域内所包含节点提交的总数据请求信息不能超过该集群域内LC的额定负载能力，LC负载约束的集群域划分算法为：

2）集群域内的控制器部署算法

将航空信息网络划分为多个集群域后，在集群域中以控制路径总故障率最小为目标进行LC部署，其目标函数如式（8.1）～式（8.8）所示，文中采用一种改进的离散粒子群算法（binary particle swarm optimization，BPSO）对目标函数进行求解，其中对离散粒子群算法的描述如下：

离散粒子群优化算法是一种基于群体智能理论的优化算法，其中用空间中的粒子表示问题的解，并根据适应度函数判断粒子的好坏，粒子依据个体最优和全局最优进行位置更新，具有收敛速度快、易实现等特点。BPSO算法中的粒子Xi由d维二进制编码组成，将粒子Xi=（xi1，xi2，…，xid）的每一维限制为0或1，其速度Vi=（vi1，vi2，…，vid）不加限制，每个位根据式（8.19）改变速度，改变后的速度转换为位变量取1值的概率，通常利用式（8.20）中的sigmoid函数计算该概率大小，在算法搜索过程中，粒子Xi通过自身和种群状态对其位置动态调整，其每一维的速度和位置计算公式如下：

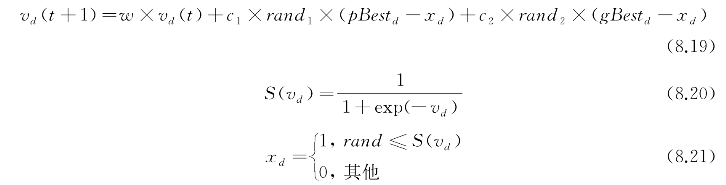
式（8.19）表示粒子的速度改变式，其中w表示粒子自身的惯性权重；c1和c2表示加速因子，rand1和rand2均表示区间［0，1］内的随机数，且两者独立；p Bestd和g Bestd分别为粒子迭代过程中的个体历史最优值和全局历史最优值；d表示维数。式（8.20）、式（8.21）表示用粒子速度更新该粒子的位置，其中用式（8.20）计算xd位置取1的概率，并通过式（8.21）改变自身位置，而利用sigmoid函数仅能体现出位取1的概率，不能体现出位改变的概率。此外，BPSO算法计算xd位值时会受前一次迭代结果的影响，并且随着迭代次数的增多，算法的随机性将增大，故该算法不能够达到理想的结果。

由上述分析可知，BPSO算法中的sigmoid函数仅能求解出粒子位取1或者取0的概率，无法求出粒子位的变化值大小。在实际生活中，人们在解决问题时通常会依赖以往的个人历史经验和社会历史经验，结合上述分析，本节提出一种改进的离散粒子群算法进行求解。

与传统粒子群算法不同，由于p Besti和g Besti中已包含粒子的历史最优信息，具有较高的可信度，因此每次粒子位的变化均取决于p Besti和g Besti的值，并可以通过设置合理的p Besti和g Besti值以避免对其过度参考。针对集群域中的LC部署问题，考虑用每个粒子表示一种LC部署方案，假设网络中共有n个节点，对于粒子Xi=［xi1，xi2，…，xin］，xin表示在第i种部署方案中节点n是否为控制节点。粒子根据p Besti和g Besti对其位置进行更新，并定义节点i在第T+1次位置更新时成为控制节点的概率为否则为假设p Besti和g Besti在寻找最优值的过程中是独立的，其中p Besti的信任度为pp，g Besti的信任度为pg，则具体的概率值为

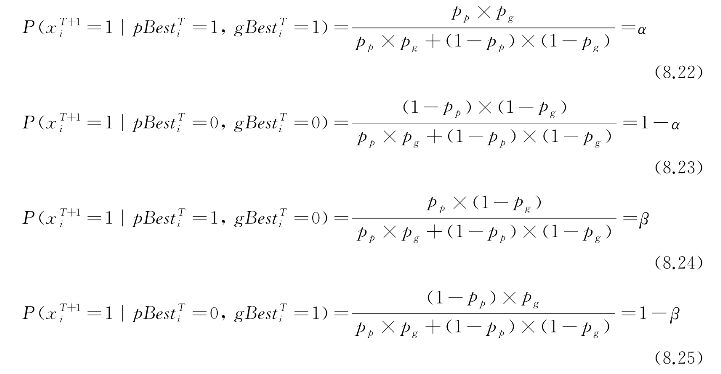
由于p Besti和g Besti均为粒子迭代过程中的历史最优值，因此其信任度高于平均值，即有pp＞0.5，pg＞0.5，同时为避免算法陷入局部最优，应保证pp＞pg，本节参考文献［20］中设置pp=0.8，pg=0.7，此时算法可获得最优性能，式中α表示当p Besti和g Besti相同时两者对xi取值的影响，β表示当p Besti和g Besti不同时两者对xi取值的影响。与改进的BPSO算法相比，BPSO需要先计算粒子的速度，在此基础上利用sigmoid函数获得位为1的概率，而改进的BPSO则直接利用式（8.22）～式（8.25）计算位为1的概率，其粒子搜索效率更高，并且改进的BPSO算法直接利用p Besti和g Besti对位的取值概率进行确定，有效地避免了前一代位值对后期取值的影响。

在寻找最优解的过程中，粒子的好坏程度用适应度函数来评价，用式（8.1）作为改进BPSO算法的适应度函数，即F=f，若某粒子的适应度函数值小，则代表该粒子所对应的解更优，否则较差，集群域内的LC部署算法具体如下：

上述LC部署算法根据式（8.19）对粒子速度进行更新，在对粒子位置更新时采用如下策略：