为了分析无人机逆向调制光通信系统传输性能,根据式(4.27)以及式(4.31)、式(4.35),对传输误码性能和中断性能进行仿真分析,同时进行蒙特卡罗仿真来验证公式的正确性,蒙特卡罗仿真中,通过系统累积分布函数的反函数,对自变量在[0,1]内随机取值,计算得到关于自变量的符合累积分布函数分布的样本,为了降低仿真中的统计不确定性,在每次仿真中产生108个随机数进行计算,仿真部分参数如表4.2所示。
表4.2 仿真参数

图4.13是光束入射角相同条件下,不同调制阶数时平均误码率随信噪比的变化关系,在仿真同时也对接收孔径分别为50 cm和75 cm条件下的系统性能进行了比较。从图中还可以看出,在同一大小的接收孔径和信噪比条件下,系统误码率随着调制阶数的增大而增大。例如,当接收端孔径尺寸为75 cm、信噪比为20 dB时,采用QPSK调制方式时的系统误码率为9×10-10;采用8PSK调制方式时的系统误码率为1.2×10-5;而采用16PSK调制方式时的系统误码率为2×10-3。同时分析图中同一调制方式下当接收端孔径尺寸不同时的误码率可以得出,随着孔径尺寸的增大,系统误码率均有所降低,例如当调制方式分别为QPSK,8PSK和16PSK时,接收端孔径尺寸为50 cm时的系统误码率分别为5×10-9,4×10-5和2.3×10-3。出现这种现象的原因是孔径平均效应削弱了接收端光强起伏,使系统误码性能有所提升,分析数据还可以发现,孔径平均效应对低阶调制时的系统误码性能改善比较明显,随着调制阶数的升高,孔径平均效应对系统性能的改善效果有所降低。
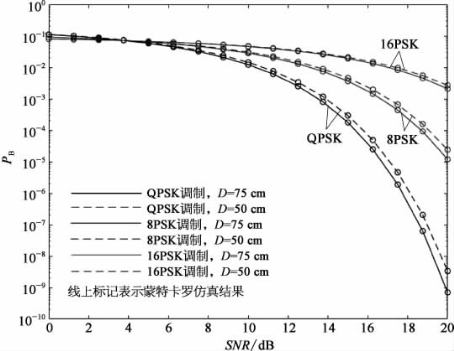
图4.13 调制阶数不同时误码率随信噪比的变化关系(入射角为25°)
图4.14为调制方式相同、入射角不同时系统误码率随信噪比变化的关系,同时比较了不同接收端孔径大小时的系统性能。分析图中数据可以得到,当入射角分别为20°,30°和40°、接收端孔径尺寸为75 cm且信噪比为20 dB的条件下,系统误码率分别为4.1×10-10,5.6×10-9和8.7×10-8;在上述条件下,将接收端孔径尺寸缩小到50 cm,其余条件不变时,系统误码率分别增长到9.5×10-10,1.3×10-8,3.9×10-7。比较以上两组数据可以发现,随着光束入射角度的增大,系统误码率逐渐升高,这是因为当光束与逆向调制端接收平面不垂直,即存在一定入射角度时,CCR的反射性能会随着入射角的增大而减小。同时研究数据发现,入射角度越大,系统误码率增长越快。这是因为入射角度越大,CCR反射性能下降越快所导致,有关这部分内容的仿真说明可参见图4.19。

图4.14 入射角不同时误码率随信噪比变化关系(调制方式为QPSK)
图4.15仿真分析了信道相关系数不同时系统误码率随光束发散角变化的规律,观察图中曲线分析反射光束发散角在50μrad附近的系统误码性能:当光束发散角为30μrad、接收孔径大小D=75 cm、信道相关系数ρI分别为0.45,0.68,0.79时,系统误码率分别为5.5×10-10,6.4×10-10和1.1×10-9;在上述条件下,仅将接收孔径大小缩小为D=50 cm时,系统误码率增大为1.4×10-9,1.9×10-9和4.1×10-9。当光束发散角增大为50μrad、接收孔径大小为D=75 cm、信道相关系数分别按照图中所示数值从小向大增长时,系统误码率分别为1.2×10-10,2.1×10-10和6.2×10-10;同样条件下,仅将接收孔径大小缩小为D=50 cm时的系统误码率分别为1.1×10-9,1.9×10-9和2.9×10-9。当光束发散角继续增大到70μrad,可以看出,两种接收孔径条件下的系统误码率又出现升高。总结上述数据变化规律可以看出,当反射光束发散角在50μrad附近时,存在一个最优光束发散角,在该发散角下系统误码性能能够达到最优。然后可以发现,信道相关系数对系统误码性能也会产生一定的影响,系统误码率会随着信道相关系数的增大而升高,这是因为信道相关系数表征着前向和返向两条链路间光强衰落互相影响的程度,当信道相关系数增大时,意味着链路之间互相影响增大,所以会出现接收端误码率升高。此外还可以看出,发散角过小时系统误码率仍然很高,这是因为在指向误差的影响下,发散角过小时系统接收端接收功率同样会减少,导致系统误码率升高。

图4.15 信道相关系数不同时系统误码率随发散角变化规律(调制方式为QPSK)
 (https://www.xing528.com)
(https://www.xing528.com)
图4.16 波束宽度分别为2.5 m和2 m时,不同调制阶数下平均误码率与信噪比的关系
当接收端光波束宽度分别为2.5 m和2 m时,系统采用不同调制阶数下的误码性能仿真如图4.16所示。分析图中曲线的变化可以发现,当信噪比较小时,波束宽度越小,系统平均误码率越低;但随着信噪比的逐渐增大,直至超过某个数值时,波束宽度更大时系统误码率更低。出现这种现象是因为低信噪比时指向误差对系统误码性能的影响较小,系统误码性能主要由接收功率大小决定,波束宽度减小使接收功率增大,接收功率越大会使接收信噪比越大,从而造成系统误码性能越好。但是随着信噪比的逐渐增大,指向误差对系统的影响逐渐明显,当信噪比较大时,波束宽度越大的系统对指向误差的抵抗能力越强,因此接收端接收功率越大,从而系统误码性能越好。例如,当系统采用8PSK调制、信噪比为10 dB的条件下,波束宽度为2.5 m时的系统误码率为1.2×10-2,波束宽度为2 m时的系统误码率为9.5×10-3;但是当信噪比增大到20 dB时,波束宽度为2.5 m时的系统误码率为1.3×10-8,波束宽度为2 m时的系统误码率为2.2×10-5。
图4.17是仿真结果为不同抖动标准差条件下平均误码率随信噪比的变化规律,仿真过程中将M-PSK调制方式下的仿真结果与已有文献中所采用的OOK调制方式下的仿真结果进行了比较。从仿真结果中可以看出,随着抖动标准差的增大,相同调制方式下的系统误码率均有所升高,并且M-PSK调制方式下的系统误码率普遍低于OOK调制方式下的系统误码率,例如:当σs=10 cm,SNR=20 dB时,系统采用QPSK,8PSK,16PSK和OOK调制方式下的系统误码率分别为1.1×10-7,3.1×10-6,2.2×10-5,1.1×10-4;当σs=20 cm,SNR=20 dB时,系统采用QPSK,8PSK,16PSK和OOK调制方式下的系统误码率则分别为1.5×10-6,9.7×10-6,4×10-5,2.9×10-4。此外,通过查阅目前所公布的有关无人机逆向调制光通信方面的实验材料,按照美国海军实验室在2001年和2009年进行的无人机逆向调制光通信实验链路性能标准(弱湍流条件下链路误码率低于10-6),可以发现,在本节仿真条件下当SNR≤20 dB时,系统采用QPSK,8PSK调制方式时是可以达到该链路性能标准的,而采用16PSK调制方式和OOK调制方式则需要系统提供高于20 dB的信噪比才可以达到该链路性能指标。需要说明的是,在该实验中,由于美军采用了“像素化”的方法将逆向调制器分割为阵列,故实验中信道相关系数是非常小的,所以在本次仿真中将ρh取值为0.1较为合适。

图4.17 不同抖动标准差条件下平均误码率随信噪比变化规律(ρh=0.1)
图4.18仿真了CCR材料折射率不同时误码率随平均信噪比的变化关系,考查了入射角度分别为20°和30°的两种情况。图中折射率数值取自3种不同的CCR材料,分别是BK glass(n=1.52),Crystal(n=2)和GaP(n=3.31)。从图中可以看出,当入射角度相同时,CCR材料折射率增大将会导致系统误码率升高。例如,图4.18(a)中,当调制方式为QPSK、接收端信噪比为20 dB的条件下,CCR材料折射率分别为1.51,2,3.31时的系统平均误码率分别为1.2×10-10,4×10-10,2×10-9,图4.18(b)中,当调制方式为QPSK、接收端信噪比为20 dB的条件下,CCR材料折射率分别为1.52,2,3.31时的系统平均误码率分别为1.5×10-8,4×10-8,1.9×10-7。分析以上两组数据还可以发现,当CCR材料折射率相同时,入射角增大会导致误码率升高,这是因为CCR的反射性能会随着入射角的增大而减小导致。

图4.18 CCR材料折射率不同时误码率随平均信噪比的变化关系
(a)入射角为20°;(b)入射角为30°
当反射光束发散角大小不同时,系统中断概率随信噪比门限变化的规律如图4.19所示。分析图中数据可以看出,当信噪比门限值一定时,随着反射光束发散角的增大,系统中断概率呈现出先降低后升高的趋势。例如,当门限值为-5 dB时,反射光束发散角依次为20,30,40,50,80,100μrad时,系统中断概率分别为6×10-1,1.5×10-1,9.1×10-7,3×10-8,1.3×10-4,6.5×10-1,这种先降低后升高的规律与图3.6所表现出的较为相似。出现这种现象的原因是因为发散角过小时,由于指向误差的影响会导致接收平面接受光功率很低,而当发散角过大时,因为接收平面光束过于发散的原因,同样会导致接收平面接收光功率很低。从图中仿真数据可以发现,在光束发散角为50μrad附近,存在最优发散角可使系统中断概率最低。

图4.19 不同发散角条件下中断概率随信噪比门限变化规律(调制方式采用QPSK)
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




