仿真及结果分析探究

利用式（3.27）、式（3.32）、式（3.34）～式（3.37）进行数值仿真计算，并通过蒙特卡罗仿真验证了数值仿真结果的准确性。在数值仿真中，设激光波长为λ=1 550 nm，FSO链路传输距离为L=100 km。针对式（3.27）、式（3.32）、式（3.34）、式（3.36）及式（3.37）中的无穷级数形式，在计算时设i=30，此时表达式可基本收敛。在蒙特卡罗仿真中，通过混合RF／FSO链路累积分布函数的反函数，对自变量在［0，1］内随机取值，计算得到关于自变量的符合CDF分布的样本，为了降低仿真中的统计不确定性，在每次仿真中产生108个随机数进行计算。在固定增益中继及可变增益中继方式下，分别给出了混合RF／FSO链路中断及误码性能分析。

1）固定增益中继

在固定增益中继方式下，中继节点到目的节点间链路（FSO链路）的平均信噪比设为10 dB，固定中继增益数值设为C=1。不同接收孔径和湍流条件下，混合RF／FSO链路中断性能随RF链路平均信噪比的变化规律如图3.3所示。其中弱湍流及中湍流强度条件下的大气结构常数分别设为2.7×10-18m-2／3及1.9×10-17m-2／3；信噪比门限值γth设为10 dB，RF链路考虑弱衰落指数条件（m=3）。由图可以看出，混合链路中断性能随湍流强度增大而降低，例如在RF链路信噪比为SNR=25 dB处，弱湍流条件下当接收孔径为D=20 cm时，混合链路中断概率为Pout=1.9×10-4，而中湍流强度条件下混合链路中断概率增加至1.4×10-3。另外由于孔径平均效应影响，随着接收孔径增大，系统中断性能得到改善。特别的，在强湍流条件下RF链路平均信噪比取SNR=30 dB时，当接收孔径D从5 cm增加至20 cm时，混合链路中断概率由9.6×10-5降低至6.7×10-5。

图3.4给出了采用固定增益中继方式，不同衰落指数及大气湍流强度条件下混合平均误码率性能的变化规律。数值仿真中采用BPSK调制方式，接收孔径设为D=20 cm。由图可知，数值仿真结果与蒙特卡罗仿真结果基本符合，验证了式（3.32）的准确性。数值结果表明，当RF链路为弱衰落指数且FSO链路为中等湍流强度时，与强RF衰落链路及弱湍流信道条件下相比，混合链路平均误码率明显降低。由此可知，固定增益中继混合RF／FSO链路中，RF链路对混合链路误码性能起主要作用。

图3.3　不同湍流强度条件下中断概率变化规律

图3.4　不同衰落指数及湍流强度条件下平均误码率变化规律

式（3.32）及式（3.34）的数值结果如图3.5所示，仿真中考虑中等湍流强度及弱RF链路衰落指数（m=3）条件。与BPSK调制方式相比，8PSK调制方式下系统误码性能较差；BPSK调制方式下混合链路平均误码率优于其他调制方式，其中，与BPSK调制方式下的数值结果相比，DPSK调制的误码性能较差，但优于NCFSK调制方式。另外，由图可知，增大接收孔径可改善系统误码性能，例如，当平均信噪比取20 dB时，BPSK调制方式下接收孔径为D=5 cm时的混合链路误码率为6.11×10-5，当接收孔径尺寸增大至20 cm，系统信噪比降低至4.37×10-5。

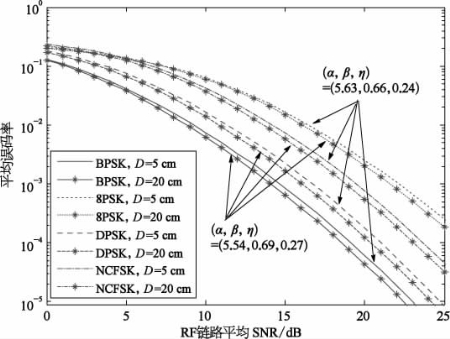
图3.5　不同调制方式下平均误码率变化规律(www.xing528.com)

2）可变增益中继

在可变增益中继方式下，设FSO链路（中继节点R-目的节点D）平均信噪比为30 dB。图3.6给出了RF链路衰落为弱湍流指数（m=3）时，不同湍流强度条件下系统中断概率变化规律及蒙特卡罗仿真结果，其中，弱湍流及中等湍流强度时的大气结构常数分别为4.5×10-18m-2／3和1.9×10-17m-2／3。由图可知，混合RF／FSO链路中断概率受大气湍流效应影响严重，具体的，当接收孔径为D=20 cm，RF链路平均信噪比取SNR=40 dB时，中等湍流条件下系统中断概率为5.8×10-3，弱湍流条件下中断概率降低为1.2×10-5。此外，当RF链路的平均信噪比增长到与FSO链路平均信噪比相等时（γr，d=30 dB），混合链路中断概率保持不变，提高RF链路平均信噪比对混合链路中断概率影响可以忽略，这种情况可根据式（3.20）中的定义进行解释。根据式（3.20）中近似表达式可知，混合RF／FSO中继系统性能主要由系统中较小信噪比决定，因此，当RF链路平均信噪比大于FSO链路平均信噪比取值（30 dB）时，混合链路的误码性能主要受中继节点R-目的节点D间链路（FSO链路）影响，出现了平均误码率保持稳定的情况。

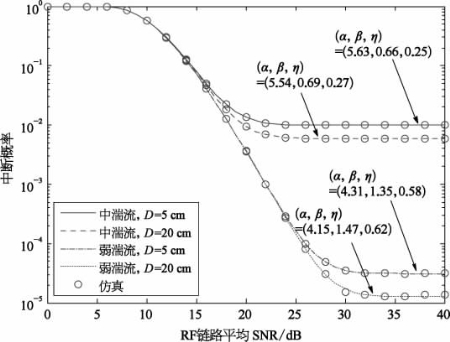
图3.6　不同湍流条件下中断概率变化规律

图3.7给出了不同接收孔径及湍流强度条件下混合链路的误码性能变化规律，其中，RF链路衰落指数设为m=3（弱RF衰落指数），大气湍流条件相关参数与图3.6中参数相同，仿真中采用BPSK调制方式。由图3.7可以看出，可变增益中继方式下，随着接收孔径增大，混合链路误码率性能逐渐改善。例如，弱湍流强度条件下，当接收孔径为D=5 cm，在平均信噪比为SNR=35 dB处，链路平均误码率为3.7×10-8；当接收孔径增大至D=20 cm，混合链路平均误码率则降低为1.2×10-8。同时可以看到，数值计算结果与相应的蒙特卡罗仿真结果相互匹配，验证了式（3.35）的理论正确性。另外，当RF链路的平均信噪比增大至30 dB（与FSO信道平均信噪比相等）及以上时，混合链路平均误码率基本保持不变；这是因为当RF链路平均信噪比大于等于FSO链路信噪比时，混合RF／FSO中继链路性能主要受较小信噪比影响，即FSO链路平均信噪比，此时RF链路信噪比对混合链路性能影响可以忽略。

图3.7　不同湍流条件下平均误码率变化规律

分别考虑弱湍流及中等湍流强度条件，不同调制方式下混合链路平均误码率变化规律如图3.8所示，仿真中接收孔径设为D=20 cm。由图中数值可知，当RF链路平均信噪比增大至30 dB时，混合链路平均误码率数值保持不变，与图3.7中变化规律一致。此外，混合链路误码率性能受大气湍流影响严重，而在弱湍流及中等湍流强度条件下，BPSK调制方式系统误码性能均优于其他调制方式。

图3.8　不同调制方式下平均误码率变化规律