Exponentiated Weibull衰落对航空平台光通信系统性能的影响

孔径平均技术具有低成本、易实现的特点，是抑制光强闪烁的有效方法。在航空平台上采用孔径平均技术，可以通过增大接收天线孔径尺寸来改善链路衰落。目前的工作都是基于Lognormal和Gamma-Gamma信道衰落模型来研究孔径平均效应的。为了准确描述各种湍流强度下有限接收孔径上的光强起伏，Barrios等提出了适用于大孔径接收的Exponentiated Weibull大气湍流分布模型。本节针对Exponentiated Weibull大气湍流分布模型，分析航空光通信链路3个主要性能指标误码率、中断概率和平均信道容量的变化规律。

1）链路模型

光波在大气湍流中传输时会由于折射率起伏使其强度发生起伏，早期的工作大都基于Lognormal或Gamma-Gamma大气湍流分布模型，为了准确描述各种湍流强度下有限接收孔径上的光强起伏，本节采用适用于大孔径接收的Exponentiated Weibull大气湍流分布模型，其概率密度分布为

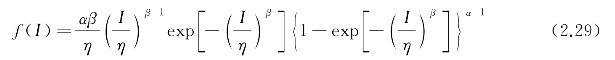
式中，α，β为与闪烁指数相关的参数，有β＞0且α＞0；η为与光强均值有关的参数，有η＜0。可通过曲线拟合的方法得到经验公式：

式中，

2）链路性能分析

（1）平均误码率。采用OOK强度直接检测时，链路平均误码率可表示为

将式（2.29）代入式（2.34），得到误码率表达式：

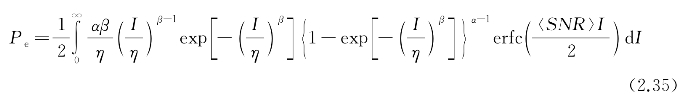
把上式中的erfc（·）和exp（·）分别用Meijer's G函数表示：

将式（2.36）代入式（2.35）得到

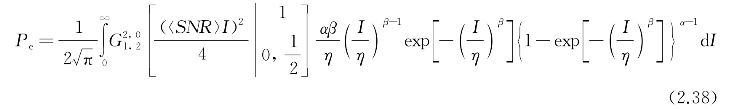
利用牛顿一般二项式定理，式（2.38）中的最后一项可以展开为

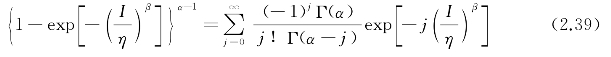
联合式（2.37）～式（2.39），平均误码率的表达式可写为

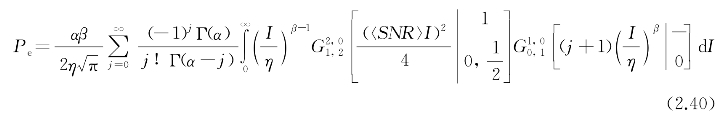
式中，为Meijer's G函数，利用Meijer's G函数的运算性质，令y=（I／η）2，通过变量转换，可得平均误码率的闭合表达式为

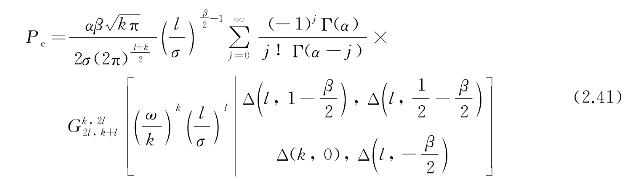
式中，ω，σ为复参数，有ω=1+j，σ=η〈SNR〉2／8；l和k为整数，满足l／k=β／2；Δ（K，式（2.41）是一个无穷级数格式，在本节中取j=30时该级数收敛。

（2）中断概率。根据中断概率定义以及接收光强起伏概率密度分布函数，可将链路中断概率表示为

将式（2.29）代入式（2.42）可得到中断概率表达式为

根据牛顿一般二项式定理对上式最后一项进行展开，并将exp（·）用Meijer's G函数表示，代入式（2.43）得

利用Meijer's G函数运算性质，可得中断概率的闭合表达式为

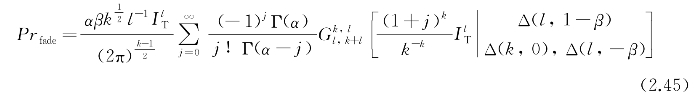
式中，l和k为整数，满足l／k=β／2。

（3）平均容量。估计通信链路的重要性能指标，假设在信道的接收端和发射端，理想的信道状态信息都可以利用，则链路的平均信道容量为

式中，B为带宽。将对数函数用Meijer's G函数表示得

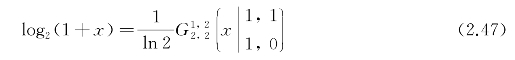(www.xing528.com)

把式（2.29）代入式（2.46），得到平均容量表达式为

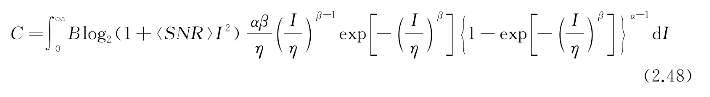
根据牛顿一般二项式定理对上式中最后一项进行展开，并把指数项和对数项用Meijer's G函数表示，将式（2.39）和式（2.47）代入式（2.48）得

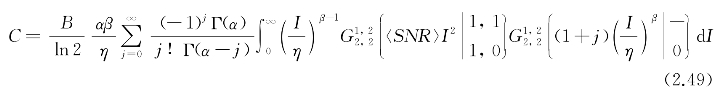
利用Meijer's G函数运算性质，可得平均容量的闭合表达式为

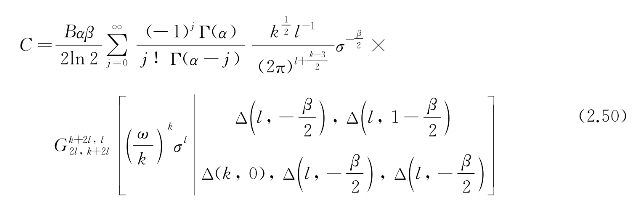
式中，ω，σ为复参数，有ω=1+j，σ=〈SNR〉η2；l和k为满足l／k=β／2的整数。

3）仿真及结果分析

（1）平均误码率。为了分析高空大气湍流和气动光学复合影响下航空光通信链路性能，本节根据以上推导的闭合表达式进行数值仿真分析。仿真中取波长λ=1 550 nm。图2.15为传输距离L=100 km、接收孔径为10 cm时，不同飞行高度条件下（即对应不同湍流强度）链路平均误码率随平均信噪比的变化关系。由图中数值可知，随着信噪比增大，误码率随之降低。在低飞行高度条件下，链路平均误码率较中、高飞行高度条件下增大。例如，在平均信噪比为20 dB处，飞行高度为10 000 m时的链路平均误码率约为2.98×10-8；当飞行高度降低为7 000 m时，平均误码率较飞行高度为10 000 m时增加了3个数量级，约为4.29×10-5；相应的，当飞行高度为5 000 m时，平均误码率较飞行高度为10 000 m时增加了4个数量级，约为2.57×10-4。图2.16分析了当飞行高度为7 000 m时，在不同传输距离条件下（分别取L=100 km，L=150 km及L=200 km），链路平均误码率的变化规律。由图可知，随着传输距离的增加，平均误码率随之增加，在平均信噪比为24 dB，传输距离为150 km时，链路平均误码率为1.29×10-6，传输距离为200 km时，平均误码率增加为2.15×10-5。

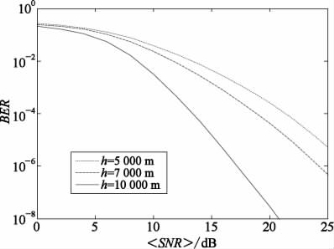
图2.15　不同飞行高度时，平均误码率随平均信噪比的变化

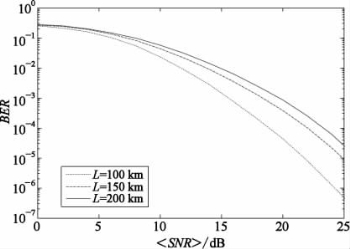
图2.16　不同传输距离时，平均误码率随平均信噪比的变化

图2.17　不同接收孔径时，平均误码率随平均信噪比的变化

当飞行高度h=7 000 m、传输距离L=100 km时，图2.17所示为不同接收孔径下（分别取点接收，D=15 cm和D=30 cm），链路平均误码率随平均信噪比的变化规律。由图2.17可知，在相同误码率要求下，点接收与孔径平均接收相比需要更大的信噪比。例如，在平均误码率要求为10-5时，点接收所需信噪比为24.3 dB，而相应的孔径平均接收D=15 cm和D=30 cm所需信噪比分别为23.8 dB及22.5 dB。

（2）中断概率。当接收光强小于设定的光强门限值IT时，认为信道衰落，IT与接收端的探测灵敏度有关。IT越小，表示探测灵敏度越高，可用分贝数FT表示光强门限值与接收端光轴上平均光强的关系，如式（2.28）中所示，显然门限参数FT越大，表示接收机探测灵敏度越高。为方便讨论，将光强进行归一化处理即〈I〉=1，对式（2.28）进行变换可得

当传输距离为L=100 km、接收孔径D=10 cm时，由图2.18可知，提高平均信噪比可降低中断概率，而中断概率随飞行高度增大而显著降低。如当中断概率为10-6时，在飞行高度h=10 000 m时链路所需门限参数与飞行高度h=5 000 m时相比降低了13 dB。这是由于大气湍流强度随飞行高度增大而降低的缘故。图2.19给出了不同传输距离条件下（100，150，200 km）中断概率的变化规律，设飞行高度为h=7 000 m、接收孔径D=10 cm，由图可知，中断概率随传输距离的增加而增大，在门限参数为FT=25 dB处，传输距离L=100 km时，中断概率约为10-8，而当传输距离L=150 km和L=200 km时，中断概率分别增大为10-6和10-5。设传输距离为100 km、飞行高度为7 000 m，中断概率随门限参数在不同接收孔径条件下的变化规律如图2.20所示。由图可知，Exponentiated Weibull衰落信道条件下，中断概率随接收孔径增大而降低，当中断概率为10-6时，对于点接收孔径所需门限参数为21 dB，而接收孔径D=15 cm及D=30 cm时，链路所需门限参数分别为19 dB及17 dB。

图2.18　不同飞行高度时，中断概率随门限参数的变化

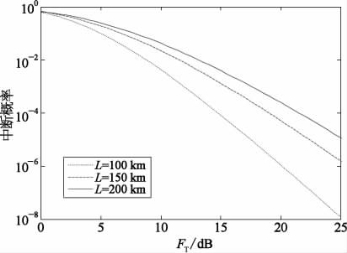
图2.19　不同传输距离时，中断概率随门限参数的变化

图2.20　不同接收孔径时，中断概率随门限参数的变化

（3）平均信道容量。本节根据式（2.50）中的数值表达式，对系统平均信道容量进行了仿真分析，仿真中选取激光波长λ=1 550 nm，给出了平均信道容量随平均信噪比、航空平台飞行高度、信道传输距离及接收孔径的变化规律。图2.21给出了平均信道容量随平均信噪比的变化规律，其中激光光束传输距离为L=100 km，航空平台飞行高度为7 000 m，Rytov参数为1.4，接收端光束参数为Θ=4.1×10-6，Λ=2×10-3，接收天线孔径为10 cm。由图中数值仿真结果可知，链路平均信道容量随平均信噪比增大而增大。当平均信噪比从SNR=6 dB增加至SNR=16 dB，平均信道容量由3 bits／s／Hz增长为5.91 bits／s／Hz。平均信道容量随传输距离的变化规律如图2.22所示，其中航空平台飞行高度为7 000 m，接收端孔径为10 cm。由图可知，大气湍流效应影响随链路传输距离增大而增加，当传输距离由50 km增大到200 km时，系统平均信道容量降低了约45.09%。

图2.21　平均信道容量随平均信噪比变化规律

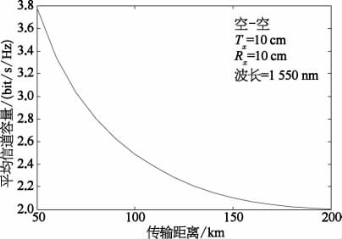
图2.22　平均信道容量随传输距离变化规律

图2.23给出了平均信道容量随接收孔径的变化关系，其中接收端光束参数设为Θ=4.1×10-6、Λ=2×10-3、传输距离为100 km、航空平台飞行高度为7 000 m。由图中数值结果可知，平均信道容量随接收孔径增大而平稳增加，由于孔径平均效应影响，大孔径接收时可对接收端湍流起伏进行平均，因此与点孔径接收端（如D=3 cm）相比光强闪烁较小，特别当接收端孔径尺寸由D=3 cm增大到D=20 cm时，链路平均信道容量从2.08 bits／s／Hz增加为3.44 bits／s／Hz，链路平均信道容量增加了约65.38%。平均信道容量随航空平台飞行高度的变化关系如图2.24所示，由图可知，平均信道容量受飞行高度影响显著，由于大气折射率结构函数与高度相关，因此在大气湍流效应影响下，飞行高度显著影响信道容量。系统平均信道随航空平台飞行高度增大而明显增加，其中当飞行高度由3 km增加至10 km时，系统平均容量由2.61 bits／s／Hz增大为6.08 bits／s／Hz。

由以上数值结果分析可知，大气湍流效应会降低系统平均容量，其中在长传输距离及小尺寸接收孔径时影响较为显著，而采用大孔径接收端可改善系统性能。

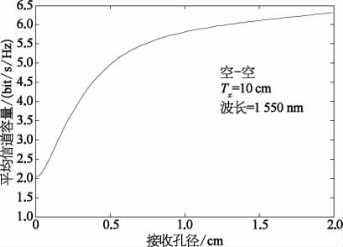
图2.23　平均信道容量随接收孔径变化规律

图2.24　平均信道容量随飞行高度变化