Gamma-Gamma衰落对航空平台间光通信系统性能的影响

高空大气环境中，由于云、雨、雾等气象条件影响，大气吸收和散射会导致激光功率衰减，同时激光光束在大气湍流中传输时由于折射率起伏变化会导致接收光强发生起伏。因此，高空大气湍流及气动光学效应对空-空链路性能的联合影响是航空光通信中亟待解决的问题。本节针对一般化的Gamma-Gamma大气湍流衰落信道，分析航空平台间光通信链路中断及误码性能。

1）链路模型

航空光通信中最典型的调制方式为二进制开关键控（on-off keying，OOK）调制，而基于相干探测方式的零差二进制相移键控（BPSK）也是航空通信中常用的调制解调模式，本节基于上述调制方式，建立航空光通信链路模型。

航空平台OOK和零差BPSK光通信发射端结构相似，其中OOK调制方式采用幅度调制器，零差BPSK调制方式采用相位调制器，因此本节中两种通信链路采用相同发射端，航空光通信链路发射端结构框图如图2.8所示。发射端由激光器（Tx-laser）、幅度及相位调制器（modulator）、光放大器（optical amplifier）组成。数据信息和激光器发射的激光光束经过电光调制器得到信号光，由光放大器进行信号光放大后通过光学天线进行传输。

图2.8　航空光通信系统发射端

OOK调制方式下，接收端由光放大器和光电探测器（PIN PD）组成，其系统框图如图2.9所示。接收到的光信号首先经过前置放大器，放大后的光信号经过光电探测器转换为电信号进行处理。零差BPSK调制方式下，接收光信号与本振激光器发射的本振光通过3-dB耦合器（3-dB coupler）实现信号混频同时放大光信号功率，经过混频后的信号进入平衡探测器进行解调获得数据信息，接收端结构框图如图2.10所示。

图2.9　OOK系统接收端

2）链路性能分析

激光在大气湍流中传输时由于折射率起伏变化会导致接收光强发生起伏，通常采用对数正态和Gamma-Gamma概率密度分布模型对光强起伏进行描述，在弱湍流情况下，光强随机起伏符合LogNormal分布，在中-强湍流情况下，光强随机起伏符合Gamma-Gamma分布，其概率密度函数为

图2.10　BPSK系统接收端

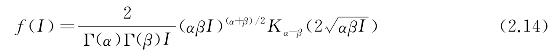
式中，I为归一化光强，Kv（·）为第二类修正贝塞尔函数，参数α和β分别为

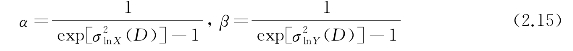
式中，和分别为接收端孔径为一固定长度D时的闪烁指数分量。

中断概率是通信链路可靠传输的度量参数，定义为接收光强小于某一光强门限值的概率，根据上式接收光强起伏概率密度分布函数，定义IT为光强门限值，可将中断概率表示为

每秒期望衰落数可定义为

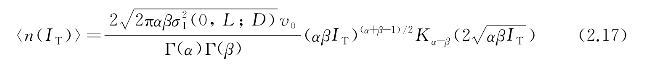
式中，根据中断概率及每秒期望衰落数两者的比值，平均衰落时间可定义为

不考虑大气湍流及气动光学效应时，激光链路信噪比（signal-to-noise ratio，SNR）可表示为

式中，is为探测器信号电流，σn为噪声功率均方差。

平均信号电流可表示为

式中，〈Ps〉为平均信号功率，η为光电转换效率，e为电荷，h为普朗克常量（h=6.63×10-34J·s），ν为光频率。

探测器输出端电流方差为

(www.xing528.com)

式中，为信号功率起伏引起的探测器散粒噪声。考虑大气湍流和气动光学效应，根据平均信噪比的定义，航空光通信链路平均信噪比可表示为

式中，Ps0为不考虑大气湍流效应的信号功率，Ps为探测器的瞬时输入信号功率。则平均信噪比可表示为

OOK调制方式下考虑大气湍流及气动光学效应影响，链路误码率可表示为

零差BPSK调制方式下，随机噪声的概率密度分布函数服从非零均值高斯分布，滤波器输出总电流包括信号和噪声两部分，其均值为is，总电流服从非零均值高斯分布，则输出端光功率为

链路中断概率为

式中，TNR=iT／σN为信噪比临界门限值，iT为门限电流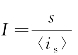，为具有平均单位的标准信号，erfc（x）为误差补函数，〈SNR〉为系统平均信噪比。零差BPSK调制方式下链路误码率可表示为

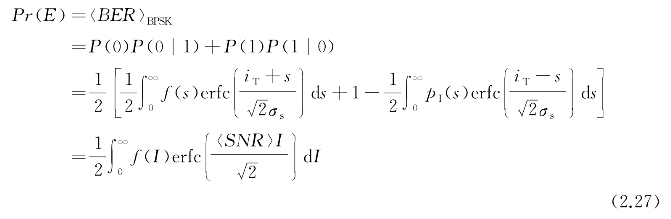
式中，P（0）和P（1）分别为发送0和1的概率，P（1|0）和P（0|1）为发送0和1时的误码概率。

3）仿真及结果分析

为了分析航空光通信系统中断性能及误码率，根据上述表达式进行了仿真分析，根据光强门限值与接收端光轴上平均光强定义门限参数FT，将低于平均光强的门限值用分贝数表示，具体表达式为）

仿真中设接收孔径为D=10 cm，激光波长λ=1 550 nm，大气湍流参数l0=0，L0=∞，波束半径W0=1 cm，选取不同传播距离L和飞行高度h进行了仿真。考虑高空大气湍流、气动光学影响以及接收端探测器噪声，基于条件概率定义，可由式（2.17）和式（2.18）得到平均衰落时间，设准频率ν0为550 Hz。

图2.11为不同飞行高度、不同传输距离条件下，中断概率随门限参数的变化关系。由图可知：随着门限参数提高，中断概率随之减小；如在门限参数FT=10 dB处，当飞行高度为10 km时，大气湍流结构常数传输距离100 km和200 km的中断概率分别为10-6和10-2；在门限参数FT=25 dB处，当飞行高度为7 km时，大气湍流结构常数传输距离100 km和200 km的中断概率分别为10-6和10-3。图2.12仿真了不同飞行高度、不同传输距离条件下，平均衰落时间随门限参数的变化情况，在门限参数FT=30 dB处，当飞行高度为10 km时，传输距离100 km和200 km的平均衰落时间分别为0.001 ms和0.01 ms；当光束传播距离200 km，航空平台飞行高度7 km时，图2.13为Gamma-Gamma大气湍流分布条件下，采用OOK强度调制直接检测和零差BPSK调制方式的激光链路误码率对比，并与自由空间大气环境下采用OOK调制方式的链路性能进行了对比。在平均信噪比为25 dB处，零差BPSK调制方式的链路误码率约为10-5，而OOK调制方式下链路误码率为10-4。

图2.11　中断概率随光强门限值变化规律

图2.12　平均衰落时间随光强门限值变化规律

图2.13　不同调制方式下平均误码率随平均信噪比变化规律

基于OOK及零差BPSK调制方式，分别考虑有无大气湍流及气动光学效应复合影响的情况，利用Optisystem软件搭建模拟航空通信系统，将计算得到的链路数据代入系统，得到OOK及零差BPSK调制方式下航空平台间激光链路误码性能变化规律。仿真中假设发射端发射功率为20 dBm（100 mW）、激光波长为1 550 nm、线宽为1 k Hz、传输距离为200 km、接收机灵敏度为-50.10 dBm、发射端及接收端天线孔径为10 cm、光电探测器响应度为0.5 A／W、低通滤波器截止频率为0.7 Hz。

图2.14给出了OOK和零差BPSK调制方式下链路眼图随传输距离变化的规律，设航空平台飞行高度为10 000 m。

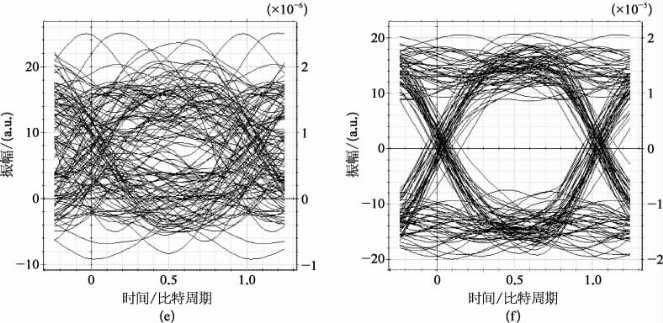
图2.14　航空光通信链路眼图

（a）OOK，自由空间（0 km）；（b）BPSK，自由空间（0 km）；（c）OOK，湍流（160 km）；（d）BPSK，湍流（160 km）；（e）OOK，湍流（200 km）；（f）BPSK，湍流（200 km）

其中，自由空间中OOK和零差BPSK系统误码率分别为1.328×10-10和2.833×10-26，如图2.14（a），（b）所示；考虑大气湍流及气动光学效应，当传输距离为160 km时，系统性能衰减较大，其中OOK调制方式下链路性能较零差BPSK链路性能差；此时上述两个调制方式的链路误码率分别上升至2.67×10-4和1.319×10-15，OOK调制方式下链路误码率远高于可靠传输可容许的最大值。当传输距离为200 km时，零差BPSK链路误码率退化至5.94×10-10，此时采用OOK调制方式的链路性能退化严重无法保证航空通信可靠性，如图2.14（e），（f）所示。纵向比较大气湍流及气动光学影响下的系统性能可知，随着传输距离增大，OOK调制方式的航空光链路性能迅速退化，而零差BPSK能够维持相对较好的误码性能，保证航空通信可靠性。