如何实现低电压穿越？

本节根据6.1节所述低电压穿越的三个不同阶段，分别介绍各阶段双馈风电机组的低电压穿越方法。

6.3.2.1 故障初始阶段的低电压穿越方法

由6.3.1节分析可知，故障初始阶段，双馈发电机的转子侧反电动势较大，易引起转子过电流和变流器直流母线过电压，从而损坏转子侧变流器。因此，第一阶段的主要控制目标是抑制转子过电流，并尽快使得定子磁链直流分量衰减为零，从而使双馈发电机进入可控区。由于实际系统的转子侧变流器容量有限，电网故障条件下，其控制能力受限，通过转子侧变流器抑制转子过电流的方法只适用于浅度故障的情况；故障较严重时，需要为双馈风电机组配备其他辅助装置，以抑制转子过电流。

本节首先分析转子侧变流器在故障初始阶段的控制极限，以转子侧变流器输出电压和电流限幅值为条件，基于最优化理论分析不同故障条件下双馈发电机组的最小转子电流，进一步得到双馈发电机组的受控区间，指出仅靠转子侧变流器无法穿越故障初始阶段；其次，分别讨论适用于浅度和深度故障的故障初始阶段低电压穿越方法，对于浅度故障，通过设计转子侧变流器的控制策略，可有效抑制发电机组转子电流和保证风电机组受控，对于深度故障，必须增加额外的硬件装置以辅助风电机组穿越故障初始阶段，本节将详细讨论不同辅助装置的结构、原理、控制方法和应用效果。需要说明的是，本节在介绍故障初始阶段低电压穿越方法时，为充分显示不同低电压穿越方法的动态控制性能，仿真和实验分析均针对低电压故障的整个过程进行，且未考虑故障持续阶段的导则要求和控制策略切换（即持续阶段仍采用初始阶段的控制方法）。故障持续阶段的低电压穿越策略将在下一小节中进行介绍。

1.故障初始阶段转子侧变流器的控制极限

由图6-15，故障初始阶段，通过控制转子侧变流器的输出电压以抵消转子侧反电动势，可有效抑制转子过电流。然而，对于通常的电压源型转子侧变流器，其输出线电压低于变流器直流母线电压，幅值受限。严重电网故障时，转子侧反电动势较大，当转子侧反电动势超过一定范围时，由于转子侧变流器输出电压的幅值限制，此时无论采用何种控制策略，转子电流都无法得到有效抑制。可见，通过转子侧变流器抑制转子短路电流存在控制极限。

故障初始阶段，转子侧变流器的控制极限可基于最优化理论进行分析^[19，20]。为突出系统的电磁本质，可选择定转子磁链为状态变量，由式（6-5）可得正向同步旋转dq坐标系下双馈发电机的磁链模型为

式中，Ψ、u、i为 双 馈 发 电 机 的 磁 链、电 压 和 电 流 空 间 矢 量，Ψ=[Ψ_sd，Ψ_sq，Ψ′rd，Ψ′rq]^T，u=[u_sd，u_sq，u′rd，u′rq]^T，i=[i_sd，i_sq，i′rd，i′rq]^T；矩阵A为

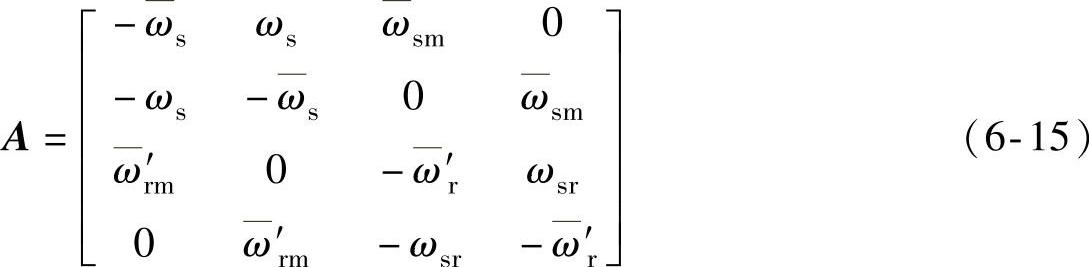
式中，ω_s，ω′_r反映了定转子磁链直流分量的衰减速度，分别表示为

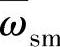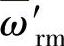，反映了定转子磁链之间的耦合强度，可表示为

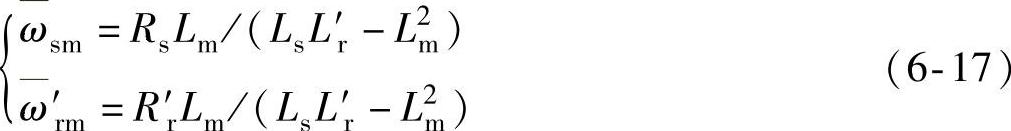
电感矩阵L的逆矩阵L^-1为

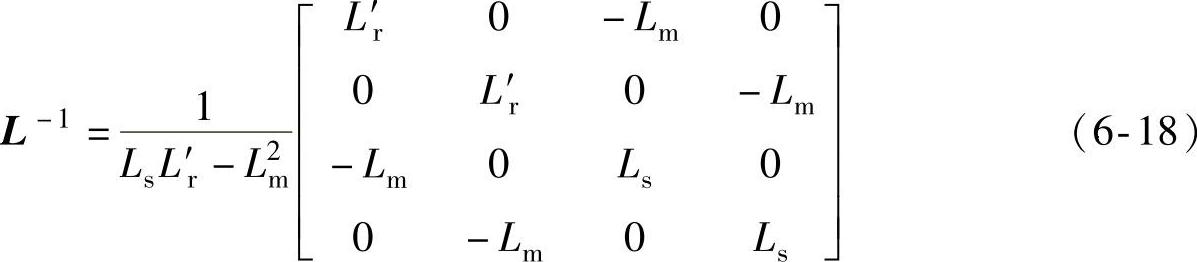
通常，定转子电阻R_s和R′_r很小，因而定转子磁链之间的耦合项ω_sm和ω′_rm也很小，为简化分析，可忽略定转子磁链之间的耦合，则矩阵A可进一步简化为

综合以上所述，系统模型式（6-14）可简化为

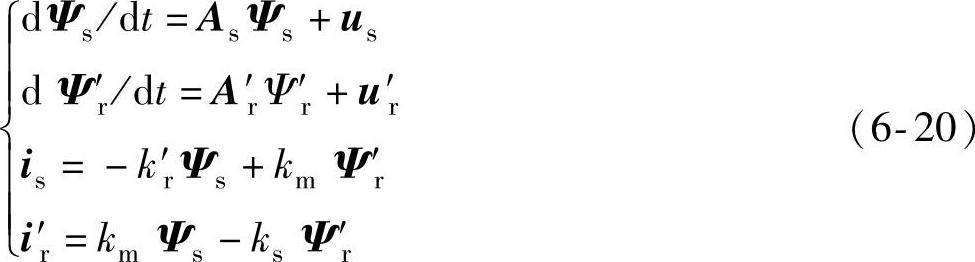
式中

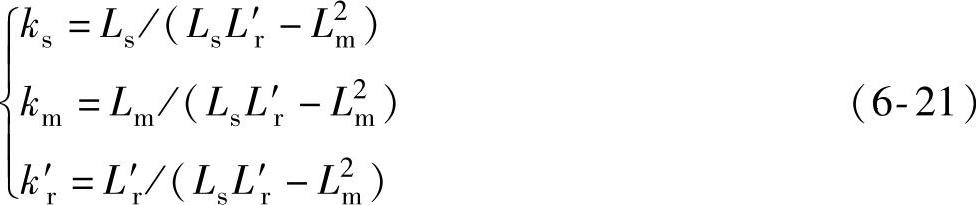
故障后，若以电网电压正序分量定向，即选择同步旋转坐标系的d轴与正序电网电压矢量重合，则电网电压在正向同步旋转坐标系下可表示为

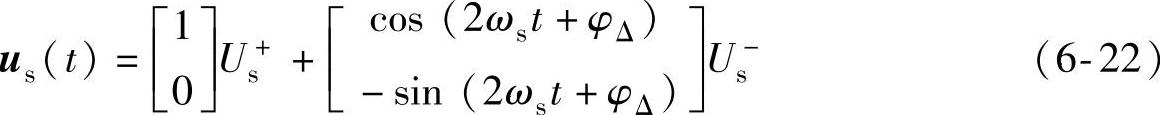
式中，t为时间；u_s（t）为双馈发电机定子电压空间矢量；U_s^+和U_s-表示定子电压正负序分量的幅值，对称故障时Us-=0；φΔ表示故障发生时正负序电压空间矢量的初始空间角度，φΔ=φ+-φ-，根据故障发生时刻和电网结构的不同，φΔ可在[0，2π）内变化。若某时刻电网发生不对称故障，故障前定转子磁链的初值为Ψ_s（0）、Ψ′_r（0），故障后电压空间矢量的正负序分量的幅值分别为U_s+（0+）、U_s^-（0+），则根据式（6-20）和式（6-22）可以得到电网故障下定子磁链的表达式为

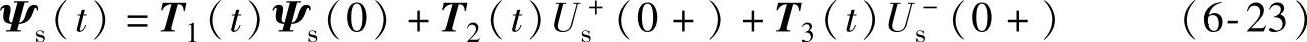
式中

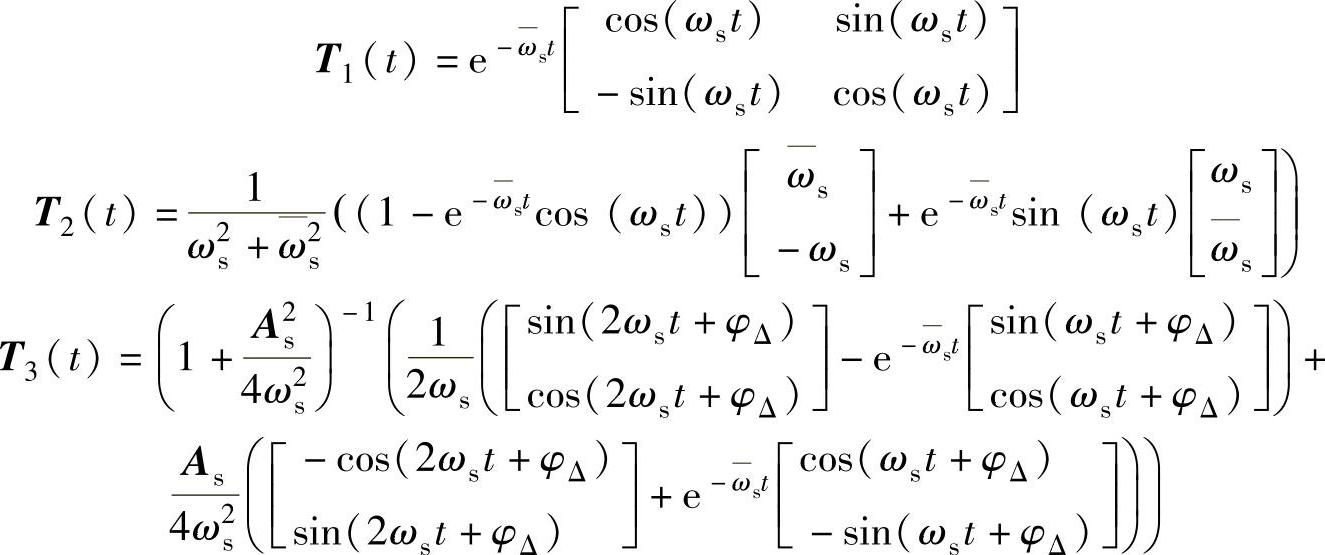
可见，定子磁链Ψ_s（t）由三部分组成，第一部分T₁（t）Ψ_s（0）为定子磁链的零输入响应，与故障发生时定子磁链的初始值有关；第二部分T₂（t）U_s+（0+）为电压正序分量的零状态响应，与故障后电压正序分量的幅值有关；第三部分T₃（t）U_s-（0+）为电压负序分量的零状态响应，与故障发生后负序电压的幅值及正负序电压空间矢量的初始角度φ_Δ有关。

转子侧变流器抑制转子电流能力的极限问题可归结为转子电压受约束条件下的转子电流最优控制问题。可设计积分型最优控制目标为

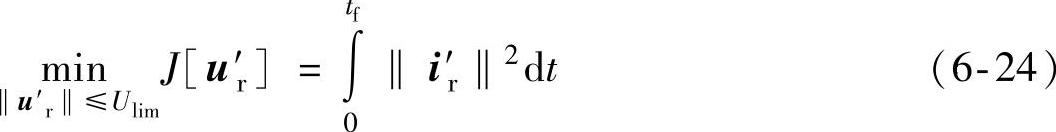
式中，J[•]为代价函数；‖•‖为矢量的模；U_lim为转子电压的最大幅值；[0，t_f]表示优化区间。上述目标的含义为在优化区间内通过控制转子电压使转子电流最小。考虑式（6-20）、式（6-23）和控制目标式（6-24），可得到转子电流抑制最优控制问题的完整描述为

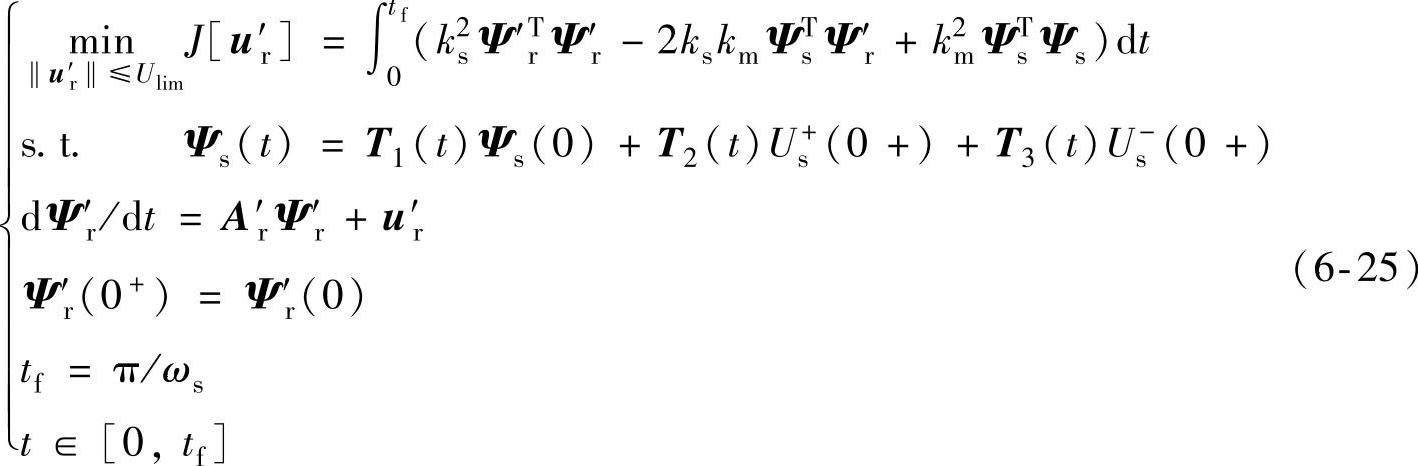
基于庞特里亚金极小值原理，可以对式（6-25）所示的最优控制问题进行求解，从而得到不同故障条件下通过控制转子侧变流器所能达到的最小转子电流，进而得到不同条件下转子侧变流器的控制极限，详细推导过程见附录C。以典型1.5MW的双馈风电机组为例，不同故障条件下，发电机最优转子电流的最大幅值如图6-17所示。以上算例中，风电机组的系统参数详见附录B表B-8，同时假设故障前风电机组工作在MPPT状态。图6-17中，x轴为故障前风力机输入机械功率P_wt，y轴表示故障前发电机定子输出无功功率Q_s，z轴为最优转子电流幅值的最大值i′_rmmax，不同曲面所标示的百分数表示发电机定子端电压的跌落深度。以三相对称故障为例，当电压跌落深度为50%时，对于不同的初始机械功率P_WT和定子无功功率Q_s，重复求解式（6-25）所表征的最优问题，可得一组最优转子电流的最大幅值i′_rmmax；改变电压跌落深度，重复上述过程，最终可得图6-17a所示的一族曲面。同理也可得到不对称故障下的最优转子电流最大值曲面，如图6-17b～d所示。

根据求取的最优转子电流最大值，可进一步分析故障初始阶段时转子侧变流器的低电压穿越能力。假设转子侧变流器可承受瞬时最大电流为2pu（取发电机转子额定电流为基准值），基于图6-17的分析结果，可得到转子侧变流器的低电压穿越可行域，如图6-18所示。需要说明的是，为了便于分析，此处以转子电流矢量的幅值是否大于2pu作为低电压穿越可行域的判别标准。也可以用最优转子电压控制量作用下转子各相电流瞬时峰值作为判别标准，两者的分析结果基本一致。以对称故障为例，不同电压跌落深度条件下，可分别计算不同P_WT和Q_s时的i′_rmmax。若i′_rmmax≤2pu，则可认为该故障条件下，转子侧变流器有能力将转子电流的最大幅值抑制在2pu以内，图6-18中用白色区域示意（可穿越区）；反之，若i′_rmmax>2pu，则说明该故障条件下，仅靠转子侧变流器无法抑制转子过电流，图中用灰色区域表示（不可穿越区）。

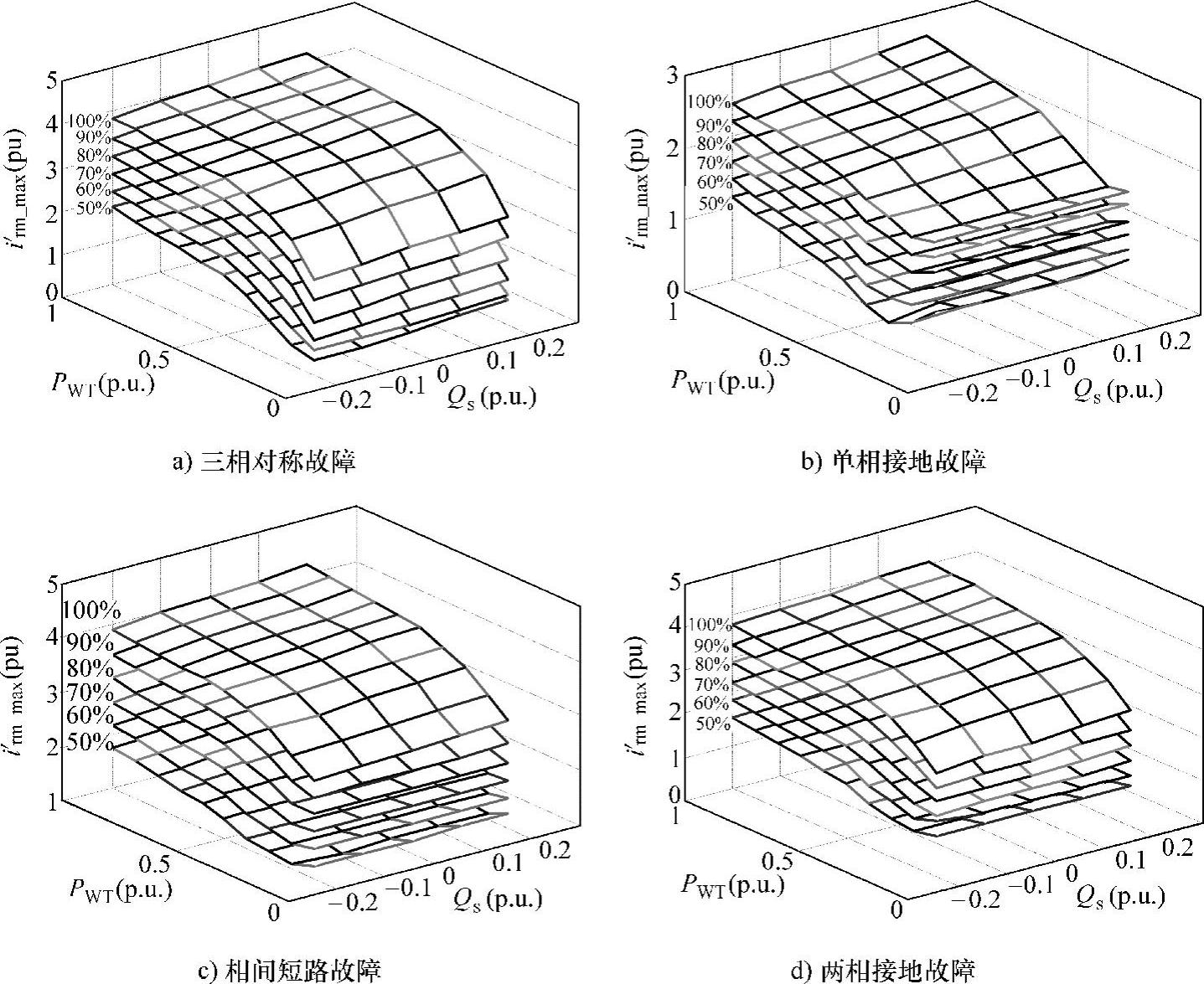
图6-17 不同故障条件下最优转子电流幅值的最大值

由图6-18所示结果，可得到以下结论：

1）不同类型的电网故障中，相间短路故障下风电机组的可穿越区域最小，低电压穿越最困难；单相接地故障下风电机组的可穿越区域最大，低电压穿越最容易。该结论与6.3.1节的分析结果一致。

2）相同故障类型和跌落深度条件下，故障前风力机输入机械功率和定子侧输出无功功率越大，低电压穿越越困难。一方面，正常运行且风速较低条件下，风力机的输入机械功率越大，其转速会越高，而由式（6-11）可知，转速升高会导致转子反电动势增加，从而增加低电压穿越难度；另一方面，风力机输入机械功率和定子侧输出无功功率较大时，故障前发电机的定转子电流已较大，故障发生后，转子更容易出现过电流。

3）不管何种故障类型，若故障较严重，仅靠改进变流器的控制方法已无法有效抑制转子过电流。此时，需要考虑增大转子侧变流器容量或增加辅助装置（如转子撬棒保护电路等）。

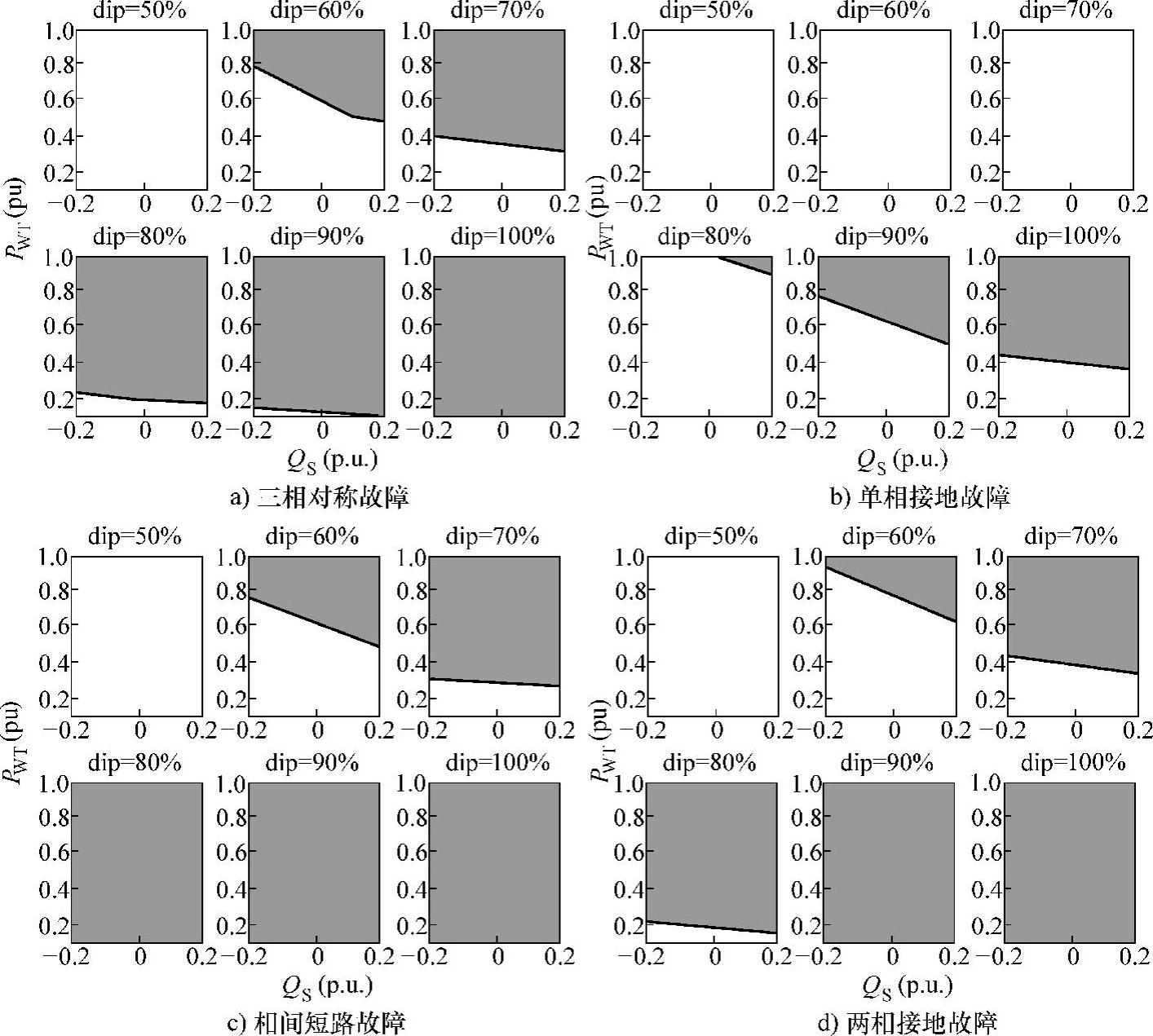
图6-18 故障初始阶段转子侧变流器的低电压穿越能力

注：dip表示电压跌落深度。

基于最优控制理论的转子侧变流器短路电流抑制能力的分析方法，可用于评估不同转子侧变流器控制策略的优劣，优化转子侧变流器的容量、控制策略及保护电路的设计。

2.轻度故障下的转子侧变流器控制方法

由上节分析可知，在轻度电网故障条件下，可通过控制转子侧变流器的输出电压，以抑制发电机的转子电流。这里所谓的“轻度”和“重度”故障是相对而言的，将通过改进转子侧变流器的控制即可完成穿越的故障称为“轻度”故障，对应于图6-18中白色区域的故障；仅采用转子侧变流器则无法穿越，而必须借助于辅助电路才能完成穿越的故障称为“重度”故障，对应于图6-18中灰色区域内的故障。值得注意的是，通过改进转子侧变流器控制，可在轻度故障下有效抑制转子短路电流，但若并网导则所要求的第一阶段时间较短，则转子侧变流器仍可能无法满足此阶段定子磁链的衰减速度要求，此时仍需要增加额外的辅助电路。

轻度故障下，转子侧变流器的典型低电压穿越方法包括基于转子电流控制和基于转子磁链控制的方法。

（1）基于转子电流控制的低电压穿越方法

基于转子电流控制的低电压穿越方法，其基本思想是通过控制转子电流，以抑制故障后定子磁链对转子回路的影响，从而避免转子过电流。基于该思路的研究成果较多^[21-26]，最具代表性的是参考文献^[21]所提出的暂态磁链补偿方法，该方法通过控制转子电流以消除故障下定子磁链中直流和负序分量对转子磁链的影响，使转子磁链只含正序分量，从而抑制转子电流。下面以该控制策略为例，对基于转子电流控制的低电压穿越方法进行介绍。

由式（6-5）中双馈发电机的磁链方程，转子磁链可表示为

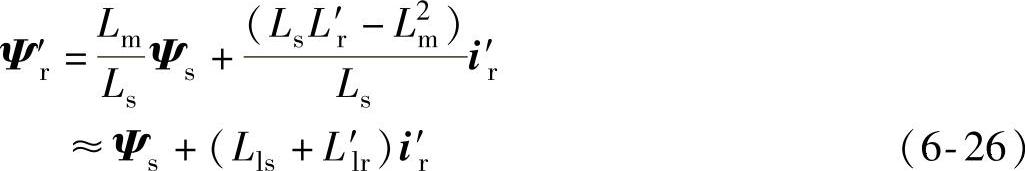
由式（6-8）可知，在电网故障下，定子磁链会产生直流和负序分量。由式（6-26），此时转子磁链中也会产生相应的直流和负序分量。将式（6-5）中所有变量经过旋转变换到转子旋转坐标系下，转子电压方程可表示为

当转子磁链中含有直流和负序分量时，它们将分别以ω_r和ω_s+ω_r的角速度反向切割转子绕组，dΨ′r_r/dt会明显增大。由于转子变流器输出电压幅值有限，当dΨ′_rr/dt的幅值超出变流器输出电压最大值时，转子侧极易产生过电流。为降低dΨ′_rr/dt，由式（6-26）可知，若控制转子电流以抵消定子磁链中的直流和负序分量，则可使转子磁链只含有正序分量；进一步，由式（6-27），转子变流器在其输出电压范围内可保证转子电流受控。

由式（6-9）可知，故障后双馈发电机定子磁链为

Ψs=Ψ_s⁺+Ψ_s^-+Ψ_sdc （6-28）

为消除故障下定子磁链中直流和负序分量对转子磁链的影响，转子电流指令可设计为

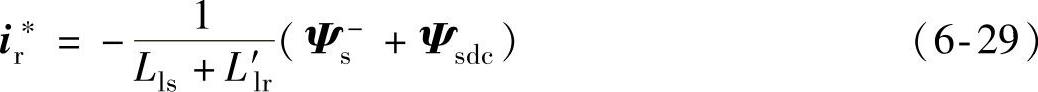
综上所述，控制系统框图如图6-19所示，控制系统由三部分组成：定子磁链估计及正负序分离、转子电流指令计算和转子电流控制。

图6-19中，定子磁链估计及正负序分离可在静止坐标系下实现，如图6-20所示。其中，定子磁链瞬时值可由下式求得：

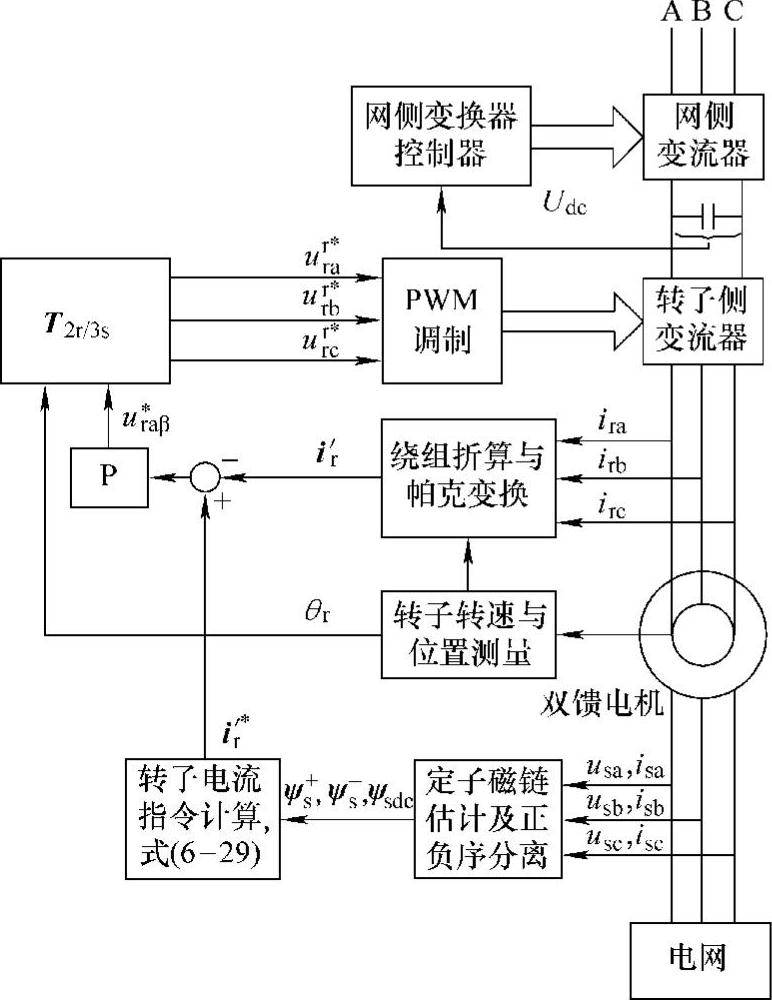
图6-19 基于转子电流控制低电压穿越方法的控制系统框图

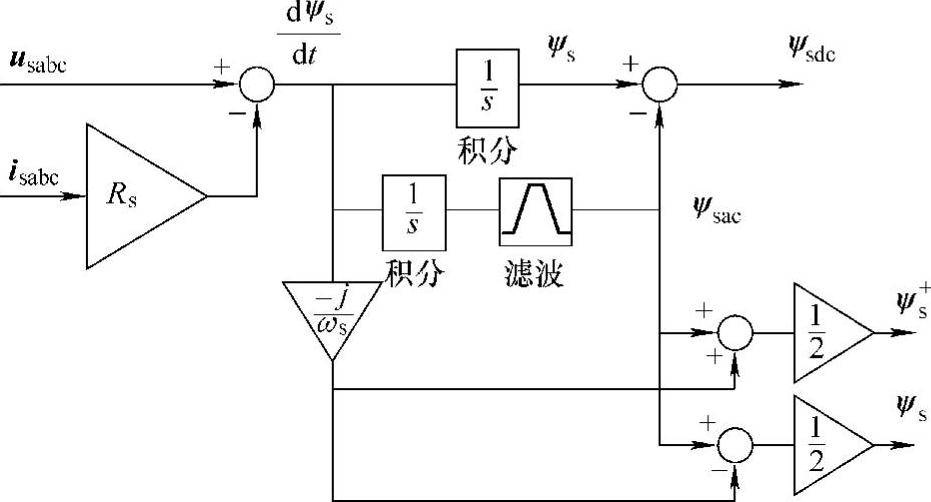
图6-20 定子磁链估计及正负序分离

静止坐标系下，定子磁链正负序分量的频率均为电网频率，而直流分量频率为0。设计二阶带通滤波器，使其中心频率为电网频率，则可有效滤除直流分量，定子磁链瞬时值与带通滤波器输出的交流分量Ψ_sac之差即为定子磁链直流分量，有

Ψ_sdc=Ψ_s-Ψ_sac （6-31）

进一步，基于式（6-32）、式（6-33）可得到定子磁链的正负序分量：

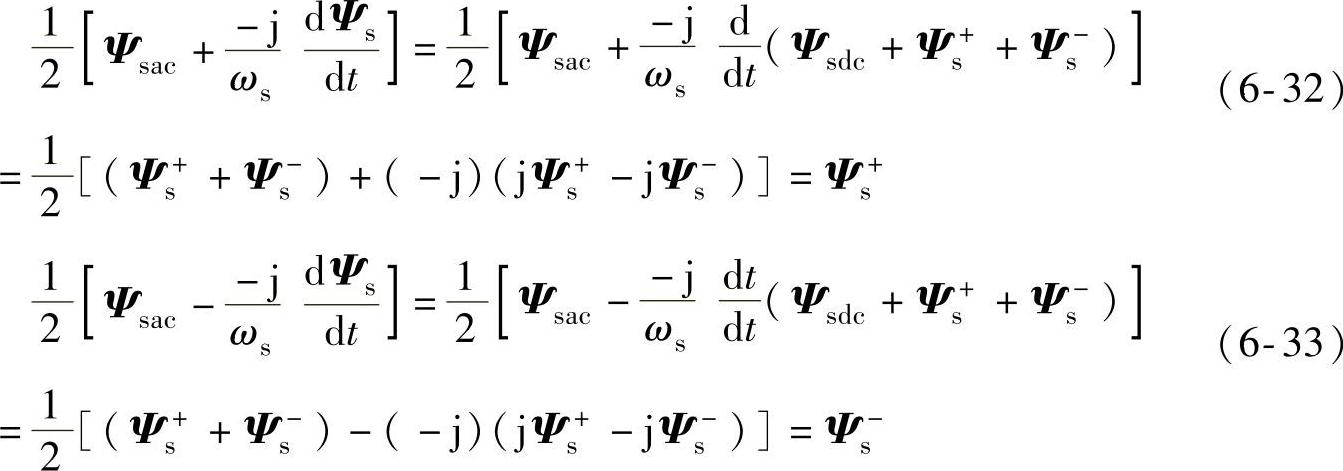
图6-19中，转子电流指令由式（6-29）得到。故障较严重时，抵消定子磁链直流和负序分量所需的转子电流较大，为了防止转子过电流，还需要对转子电流指令进行限幅；此外，与直流分量相比，定子磁链负序分量对转子回路的影响更大，严重故障下，还可以设计转子电流指令以优先抵消定子磁链负序分量。

图6-19中，转子电流的闭环调节在两相定子静止坐标系下实现，由于转子电流指令含有交流分量，因而控制框图中采用比例调节器；其输出的转子电压指令需要变换到转子旋转坐标系下，经调制后再对转子侧变流器进行控制。

在三相对称故障和单相接地故障条件下，基于转子电流控制低电压穿越方法的仿真结果如图6-21所示。仿真中，三相故障下，机端电压跌落深度为70%；单相接地故障下，a相电压幅值跌落90%；双馈发电机参数见附录B表B-8。电网电压正常时，转子侧变流器采用矢量控制，风力机输入机械功率为0.67pu，定子侧输出的无功功率为0；t=0.1s时电网发生故障，检测到故障后，转子侧变流器切换为基于转子电流控制的低电压穿越方法；t=0.3s时故障切除，机端电压恢复正常；t=0.5s时转子侧变流器恢复为故障前控制方法。为限制直流母线电压不超过1.1pu，变流器直流母线两端并联可控制动电阻。

假设转子瞬时过电流最大值为2pu，由仿真结果可见，在两种电网故障下，暂态磁链控制都可以限制转子电流，保证变流器安全运行。对称故障条件下，定子磁链只含直流分量，暂态磁链补偿方法可完全抵消其影响，转子侧变流器输出电压较低；不对称故障条件下，定子磁链还包含负序分量，由于转子侧变流器对转子负序电流的控制能力较弱，其输出电压明显增大。对于轻度故障，暂态磁链控制可有效降低故障期间注入直流母线的能量，抑制母线电压的升高。然而，故障期间，尤其在不对称故障条件下，电磁转矩振荡较大，对机械传动链冲击较大，严重时会导致风电机组的保护切机。此外，故障较严重时，定子磁链的直流分量和负序分量较大，实现暂态磁链补偿所需的转子电流较大，存在不可控区域。

（2）基于转子磁链控制的低电压穿越方法

除了对转子电流直接控制以避免其过电流，也可对转子磁链直接控制，间接抑制转子电流，典型方法为参考文献[27]提出的磁链跟踪控制方法，其核心思想是在电网故障时，控制转子磁链跟踪定子磁链变化，间接抑制转子电流。

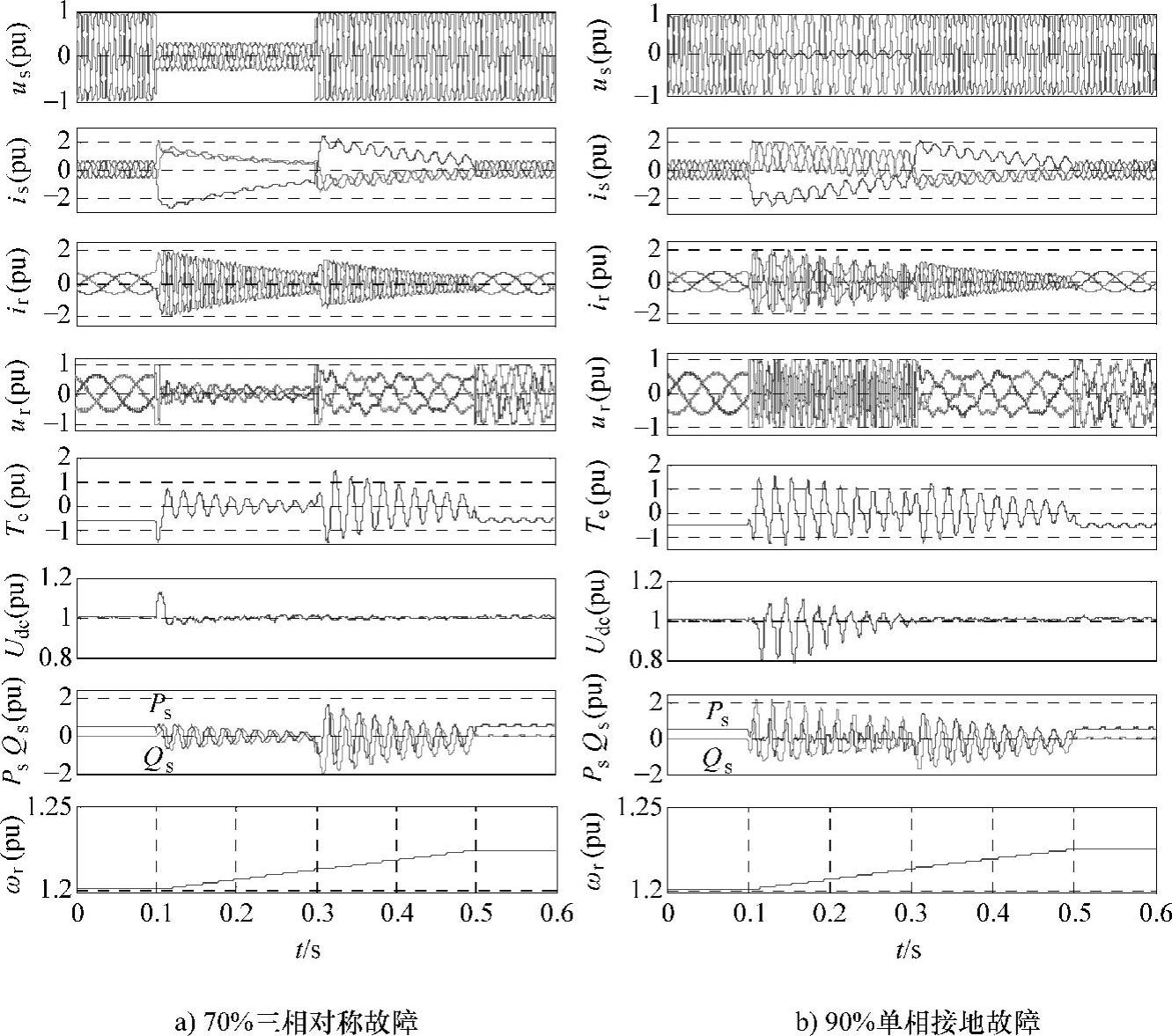
图6-21 基于转子电流控制低电压穿越方法的仿真结果

由式（6-26）所示的双馈发电机磁链方程可知，转子电流可以表示为

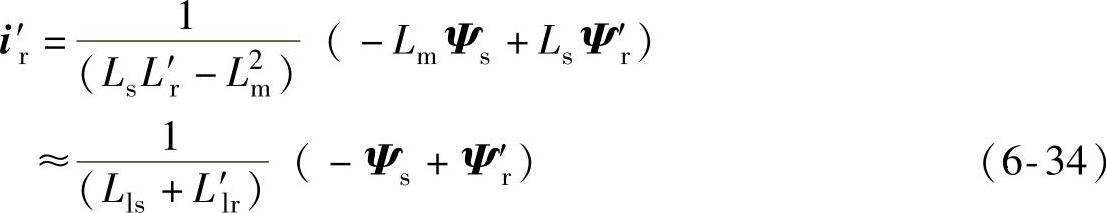
可知，转子电流由定子磁链和转子磁链的差值决定，电网故障时，定子磁链会产生直流和负序分量，若转子磁链不能及时跟随定子磁链的变化，两者差值变大，转子易产生过电流。因此，检测到电网故障时，可控制转子磁链跟随定子磁链，只要两者的差值在允许范围内，转子电流就可得到有效抑制。

由图6-15和式（6-27），忽略较小的转子电阻时，转子电压可近似表示为

故障下，定子磁链含有较大的直流和负序分量，若控制转子磁链完全跟踪定子磁链，由式（6-35）可知，所需转子电压较高。通常，转子电压受变流器直流母线的限制，为合理利用直流母线电压，可控制转子磁链跟踪部分定子磁链，如

Ψ′_r∗=k_TΨ_sk_T∈（0，1） （6-36）

式中，k_T为跟踪系数。将式（6-36）分别代入式（6-34）和式（6-35），可以得到磁链跟踪控制下的转子电流和电压为

增大k_T可降低转子电流，但所需的转子电压相应增大；减小k_T可降低控制所需的转子电压，但转子电流会增大。因而，参数k_T对控制性能有很大影响。若要保证故障条件下转子侧变流器的安全运行，转子电流需满足

式中，I′_{rm_max}为转子电流的最大幅值；I_max为经过绕组折算的转子变流器所能承受的最大电流值。考虑到转子电压的限制条件，在保证不等式（6-39）成立的条件下，应尽可能减小k_T，以降低控制所需的转子电压。

由式（6-37）可知，磁链跟踪控制下，当定子磁链幅值最大时，转子电流的幅值最大。电网故障时，定子磁链最大值出现在故障初始时刻，由于磁链不能突变，此初始值即为故障前磁链值，其幅值可近似表示为

因而

将式（6-41）代入式（6-39），可得k_T最小值k_{T_min}为

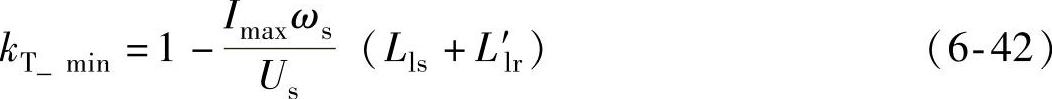
为提高暂态过程的控制效果，k_T一般选为k_{T_min}的1.2～1.5倍。暂态磁链控制也可以用于抑制故障恢复阶段的转子过电流，此阶段定子磁链会逐渐增大，此时需要适当增大k_T，以快速抑制转子电流，此时可选k_T为k_{T_min}的1.5～2倍。

转子磁链控制方法的控制框图如图6-22所示，控制系统包括三部分：定转子磁链估计、转子磁链指令计算和转子磁链控制。

图6-22中，定转子磁链估计可由定转子磁链方程式计算得到，由于磁链跟踪的目标仅仅是控制转子磁链接近定子磁链，因而该方法对系统参数和电流测量的准确度要求并不高。转子磁链控制通过闭环调节使转子磁链跟随其指令。由双馈发电机磁链模型^[20]，同步旋转坐标系下转子磁链-电压方程式可表示为

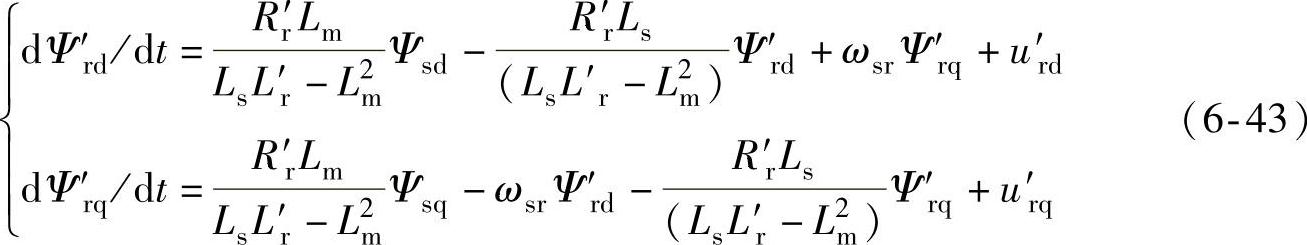
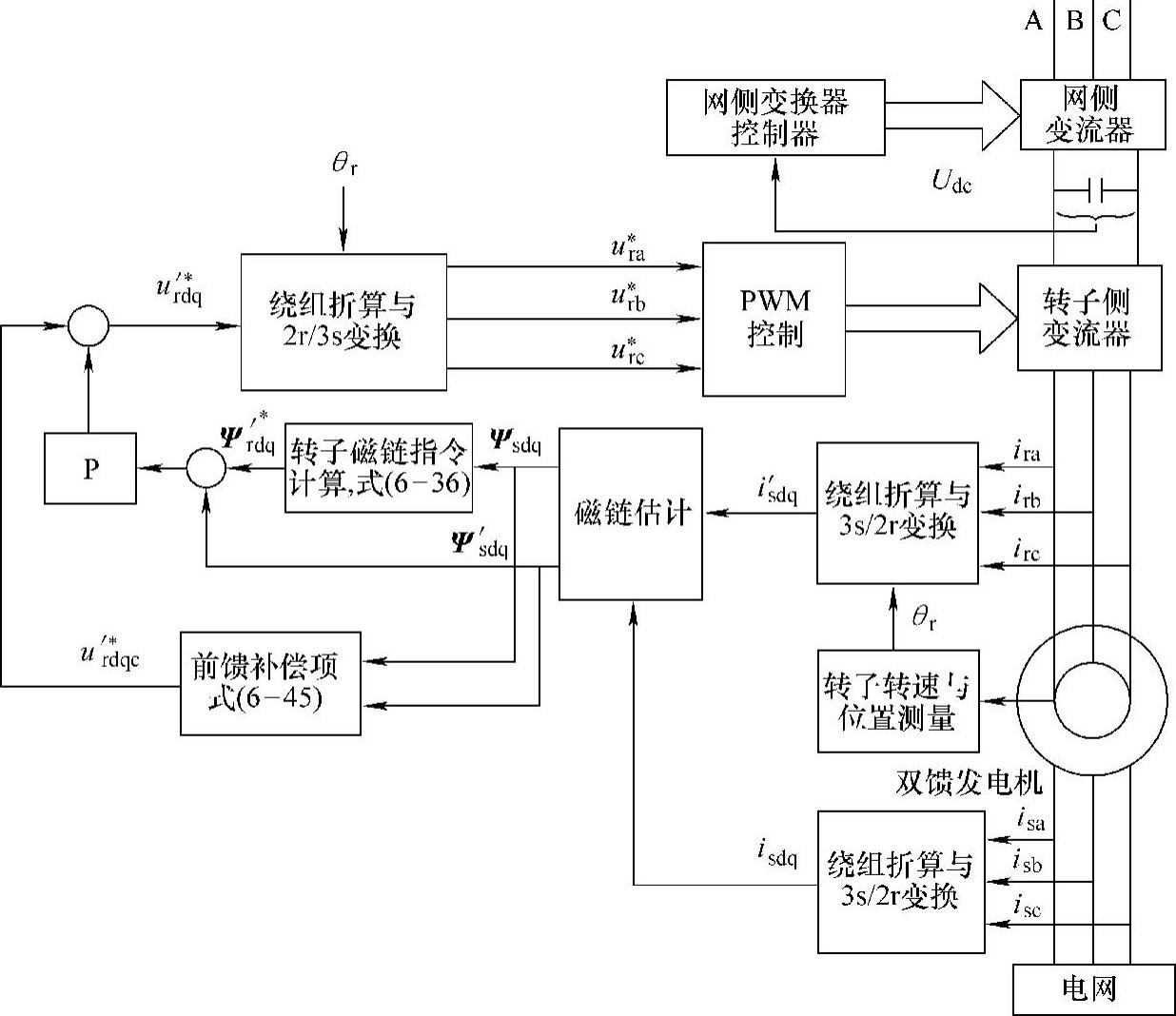
图6-22 磁链跟踪控制的系统框图

引入前馈解耦项后，系统可分解为两个独立的一阶惯性环节。考虑到在同步旋转坐标系下，转子磁链指令含交流分量，可采用比例调节器进行闭环控制，转子电压指令可表示为

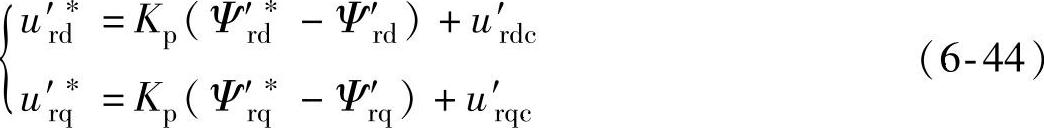
式中，K_p为比例调节系数，u′_rdc和u′_rqc表示前馈补偿项，分别为

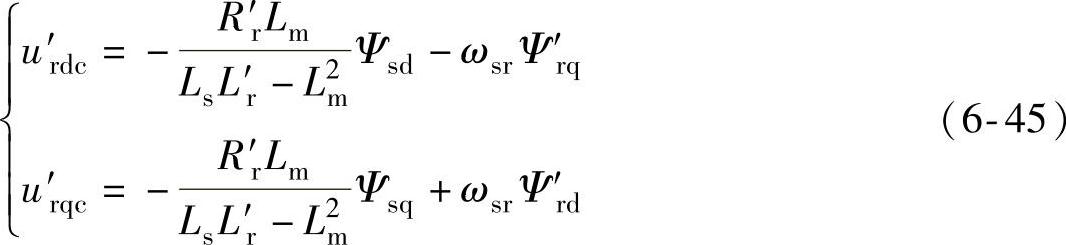
在三相对称故障和单相接地故障条件下，磁链跟踪控制的仿真结果如图6-23所示。仿真中，三相故障下，机端电压跌落深度为70%；单相接地故障下，a相电压幅值跌落深度为90%；双馈发电机参数见附录B表B-8。由式（6-42）可得，k_{T_min}=0.45，仿真中，故障发生时取k_T=0.55，故障恢复时取k_T=0.85。

由图6-23结果可知，在电网发生对称和不对称故障时，磁链跟踪控制都可有效抑制转子过电流和直流母线过电压。与基于转子电流控制的低电压穿越方法相比，磁链跟踪控制下，双馈发电机转子电流衰减速度较快，电磁转矩脉动较小。

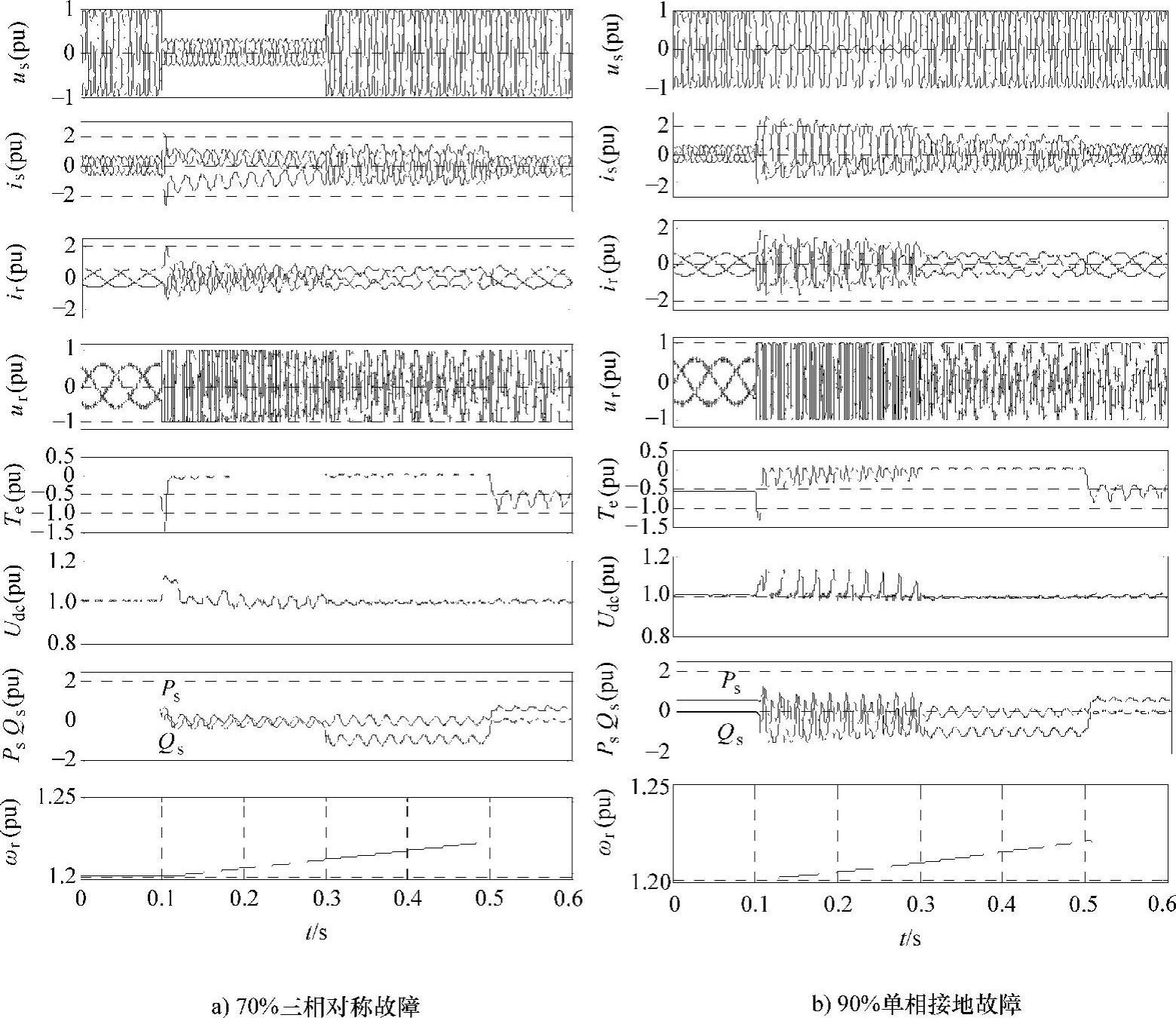
图6-23 电网故障下磁链跟踪控制的仿真结果

双馈发电机的电磁转矩为

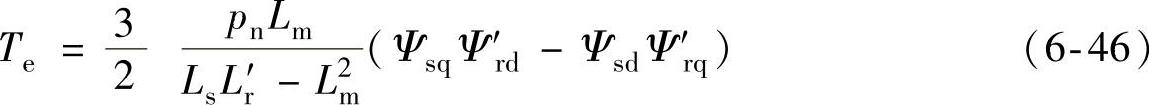
将式（6-36）代入式（6-46），可得T_e=0，可见在磁链跟踪控制下，若转子磁链跟随控制指令，则电磁转矩恒为0，即该方法可有效抑制电磁转矩振荡。实际应用中，尤其在严重故障条件下，变流器输出电压限制会影响转子磁链的跟踪效果，如图6-23b所示，电磁转矩仍存在一定波动。此外，相比于基于转子电流控制的低电压穿越方法，磁链跟踪控制下转子磁链中直流和负序分量含量更大，因此其控制所需的转子电压要要高于暂态磁链控制^[27]。

对称故障且电压跌落深度为50%、不同跟踪系数k_T条件下的系统仿真结果如图6-24所示。可知，增大k_T可以降低故障期间转子电流的大小，但是所需转子电压幅值会变大，与前面的理论分析一致。

在实验室搭建小容量实验平台对磁链跟踪控制方法进行验证，系统参数详见附录B表B-9。实验中，电网故障采用本书8.2.1.2节图8-4b所介绍的电压跌落发生器模拟；风力机由直流电动机模拟，其与双馈发电机同轴相连，控制直流电动机工作在转速模式下，带动双馈发电机发电运行；转子侧变流器的控制由DSP芯片实现，变流器的采样和开关频率均设置为12.5kHz。

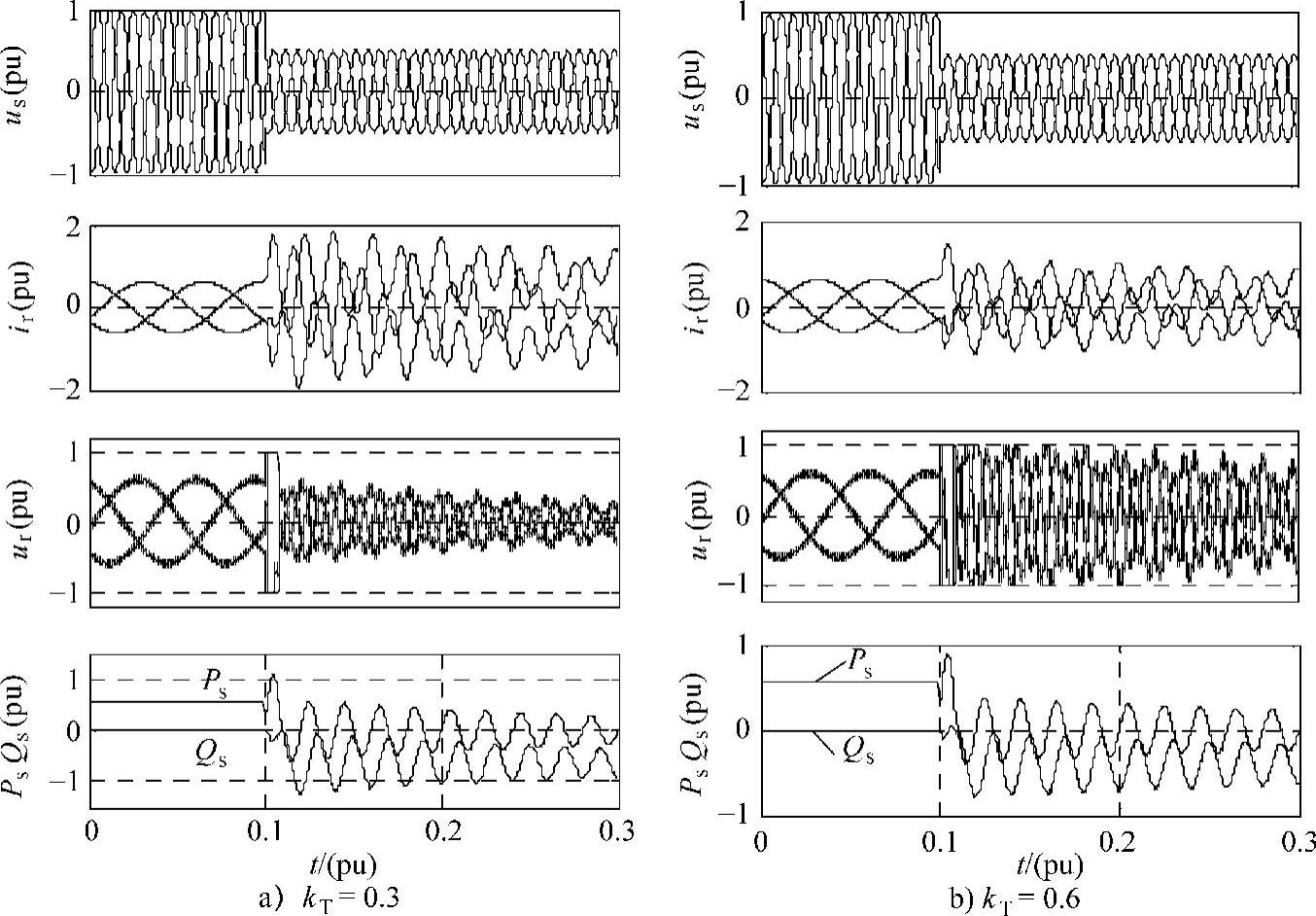
图6-24 50%对称故障下k_T取不同值时的仿真结果

电网电压正常时，定子侧输出有功功率为0.2pu，无功功率为0。t=0.05s时电网发生故障，在三相对称故障且电压跌落深度为90%、单相接地故障且A相电压跌落深度为90%两种条件下，磁链跟踪控制的实验结果如图6-25所示。由图可见，实验与仿真结果吻合，进一步验证控制策略的有效性及可行性。需要说明的是，实验中所采用的双馈发电机容量较小，与兆瓦级双馈发电机相比，转子电阻和漏感都较大，故障下更有利于转子短路电流的抑制，因此实验中在90%电压跌落深度的对称故障下仅利用转子侧变流器即可有效抑制转子短路电流，这在实际兆瓦级双馈发电机中是难以做到的。

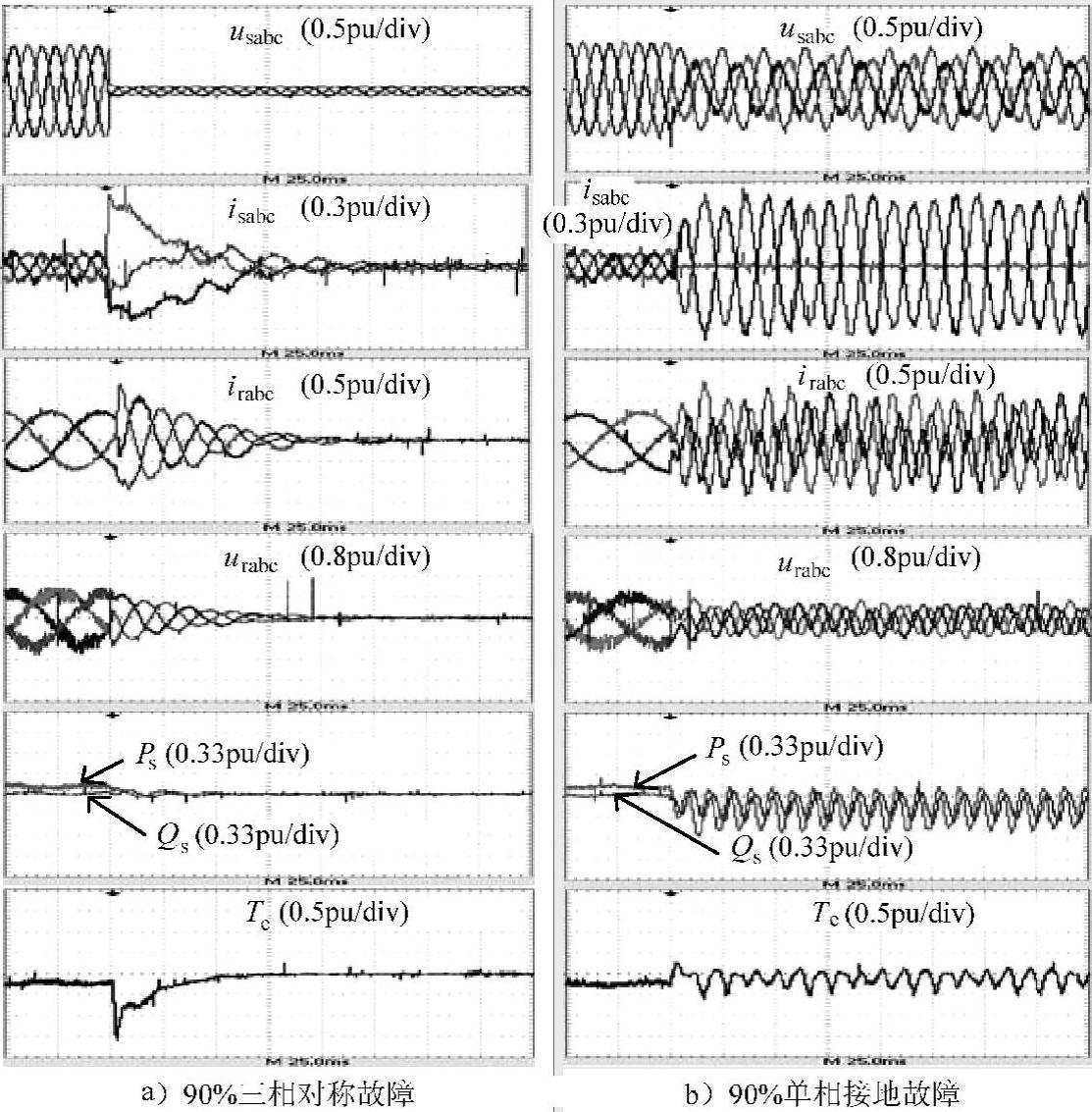
图6-25 电网故障下的磁链跟踪控制的实验结果

3.深度故障下的控制方法

由“故障初始阶段转子侧变流器的控制极限”分析可知，由于变流器容量限制，严重电网故障下，仅通过转子侧变流器无法有效抑制双馈发电机的转子电流，此时必须增加辅助装置以实现双馈发电机对故障初始阶段的穿越。商业化机组上常用的辅助装置包括转子侧撬棒电路和直流撬棒电路（变流器直流母线上并联的斩波器（Chopper）电路）；此外，也有学者在研究中提出定子侧连接无源电阻网络或定子侧串联动态电压恢复器等方法，下面对这几种方法分别进行介绍。

（1）转子侧撬棒（Crowbar）电路

在双馈发电机转子侧增加撬棒电路来保护转子侧变流器，是目前商业化双馈风电机组上广泛应用的低电压穿越技术。其基本工作原理是：若检测到转子过电流或变流器直流母线过电压，转子侧变流器停止工作，同时将撬棒电路接入双馈发电机的转子回路，将过剩的能量消耗在撬棒电阻上。

撬棒电路根据所用开关器件的不同，可分为被动式和主动式两种结构。被动式撬棒电路也称为晶闸管撬棒电路，其典型拓扑如图6-26所示^[28]。其中，图a为双向晶闸管型撬棒电路，其结构最简单，但由于采用不对称结构，动作后双馈发电机转子电流会出现较大的直流分量，因而并不实用[29]；图b为不控整流加晶闸管型撬棒电路，晶闸管数量少、成本低。由于采用半控型器件，被动式撬棒电路一旦动作后难以关断，考虑到双馈发电机转子电流频率通常较低，被动式撬棒电路动作时间较长，难以满足并网导则在故障初始阶段的相关要求，目前已逐渐被主动式撬棒电路所代替^[30]。

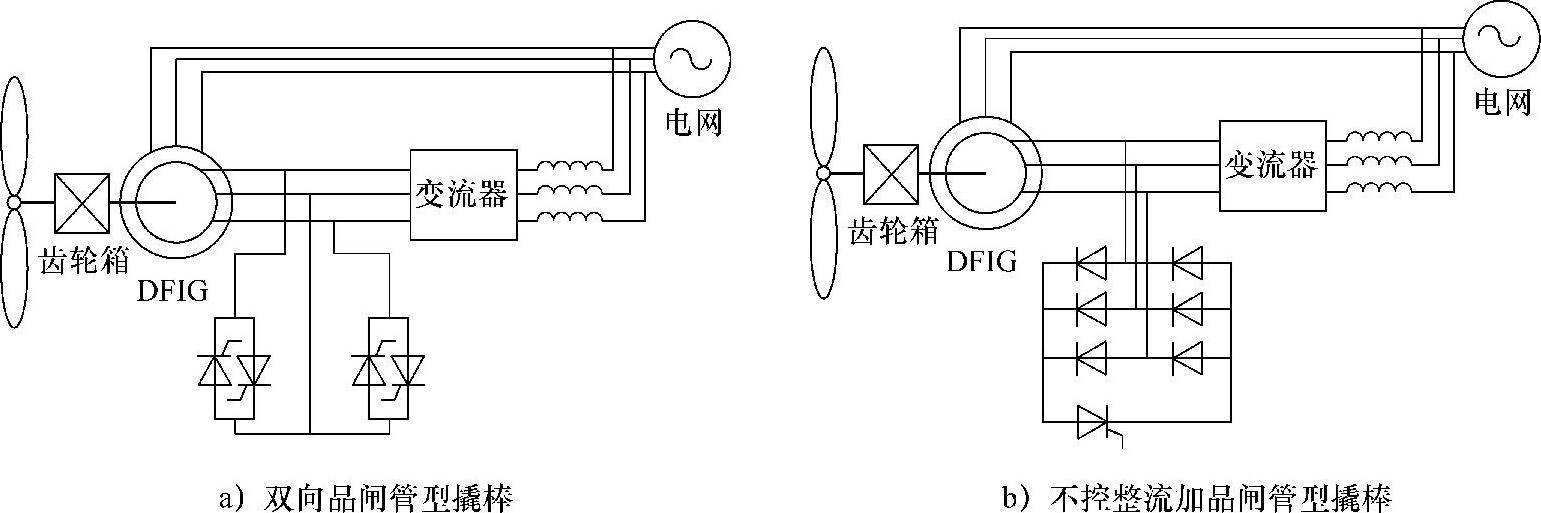
图6-26 被动式撬棒的两种拓扑

与被动式撬棒电路相比，主动式撬棒电路采用门极关断（Gate-Turn-Off，GTO）晶闸管或绝缘栅双极型晶体管（IGBT）等全控型器件，其典型拓扑如图6-27所示^[28，31]。由于采用全控型器件，主动式撬棒电路动作后可随时从转子侧切除，易于满足故障初始阶段的并网导则要求。

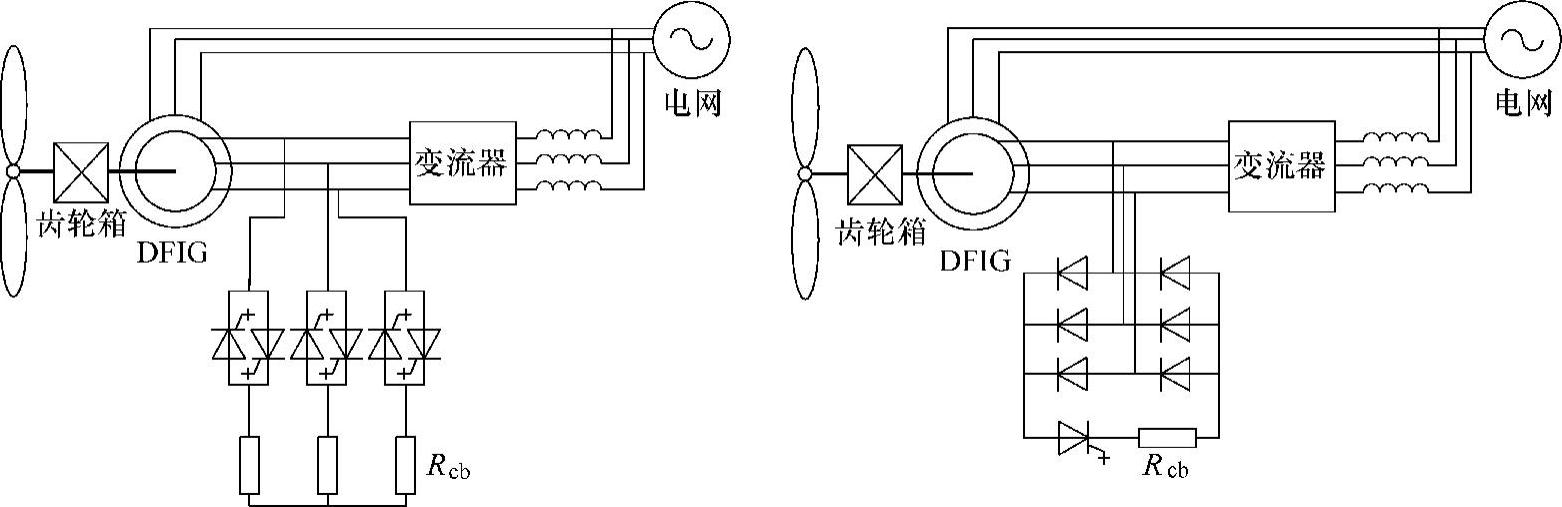
图6-27 主动式撬棒的两种拓扑

需要注意的是，图6-27所示的撬棒电路中，能耗电阻R_cb的阻值选取非常重要，阻值太小，则不能有效抑制转子过电流；阻值增大，可加快转子电流的衰减速度，但会增加转子电压。通常，撬棒接入瞬间，转子侧变流器虽停止工作（电力电子器件的驱动脉冲已封锁），考虑到连接转子侧变流器与发电机转子的机械开关存在动作延时，转子侧变流器并不能立刻与双馈发电机转子断开连接，若撬棒阻值过大，较大的双馈发电机转子端电压会迫使转子侧变流器的反并联二极管导通（工作在不控整流状态），并向直流母线电容充电，仍可能引起转子侧变流器过电流及直流母线的过电压。可见，撬棒电阻阻值的选择应使撬棒电阻上产生的转子电压低于所允许的最大转子电压。

下面介绍一种简单有效的撬棒电阻设计方法^[32]。记直流母线电压为U_dc，当撬棒上所产生的转子线电压的瞬时值超过U_dc时，转子侧变流器将工作在不控整流状态。令双馈发电机转子绕组所允许的最大转子电流有效值为I_r__lim，此时在撬棒电阻上产生的线电压幅值可表示为

为了避免撬棒动作后转子侧变流器工作在不控整流状态，转子电流有效值达到上限值I_r__lim时，转子线电压幅值应低于U_dc。由此，撬棒电阻阻值的选取应满足

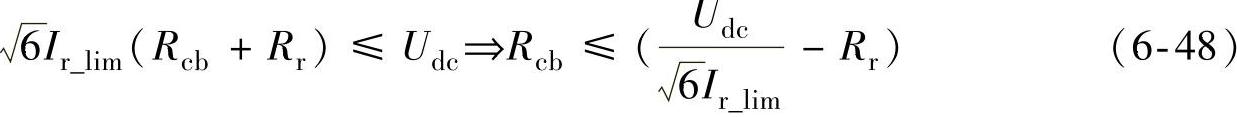
考虑到双馈发电机的低电压穿越能力及转子侧变流器反并联二极管过电流能力等因素，撬棒电阻阻值可在式（6-48）的基础上增大1.3～1.7倍。

转子撬棒保护电路方法可应用于严重电网故障的条件，其控制简单可靠，在实际工程中得到广泛应用。值得注意的是，撬棒接入时，双馈发电机将失去可控性，以异步发电机方式运行，会从电网吸收大量无功功率，不利于电网故障的恢复；同时，撬棒动作时，双馈发电机电磁转矩振荡较大，将对系统传动轴产生较大的机械冲击^[33，34]。

（2）直流撬棒电路

在变流器直流电容上并联斩波器电路来保护转子侧变流器，也是目前商业化双馈风电机组上广泛应用的低电压穿越技术。其基本工作原理是：若检测到转子过电流或直流母线过电压，则转子侧变流器停止工作，同时控制直流斩波器开关管的占空比，将多余能量消耗在耗能电阻上。其典型拓扑如图6-28所示^[35]，该电路工作时，转子电流会经过转子侧变流器反并联二极管流向直流侧，考虑到标准设计下转子侧变流器反并联二极管容量有限，该电路还需要在转子侧变流器的开关器件两端额外并联二极管，以提高其过电流能力。若以储能系统代替图6-28中的耗能电阻^[28]，还可进一步降低损耗、提高系统效率，其拓扑如图6-29所示，图中，储能元件不局限于电池，也可是超级电容、超导线圈等其他元件。由于储能装置可输出一定有功功率，与耗能电阻相比，该方法可更有效地抑制直流母线电压的波动，显然该方法的成本也更高。

在三相对称故障且电网电压跌落深度为80%的条件下，分别采用转子和直流撬棒电路的仿真结果如图6-30所示。仿真中，转子撬棒阻值根据参考文献[32]所述的方法进行选取，双馈风电机组参数见附录B表B-8。尽管两种方法所采用的电路结构不同，但其本质相同，都是通过接入能耗电阻消耗掉多余能量，以抑制转子过电流和直流母线过电压。由图6-30可见，两种方法下，双馈发电机的动态响应相似。以上两种方法在当前的商业化机组中均得到了应用，如Repower公司、Nordex公司均采用了转子撬棒方案；VESTAS公司则采用了直流撬棒的方案^[38]。

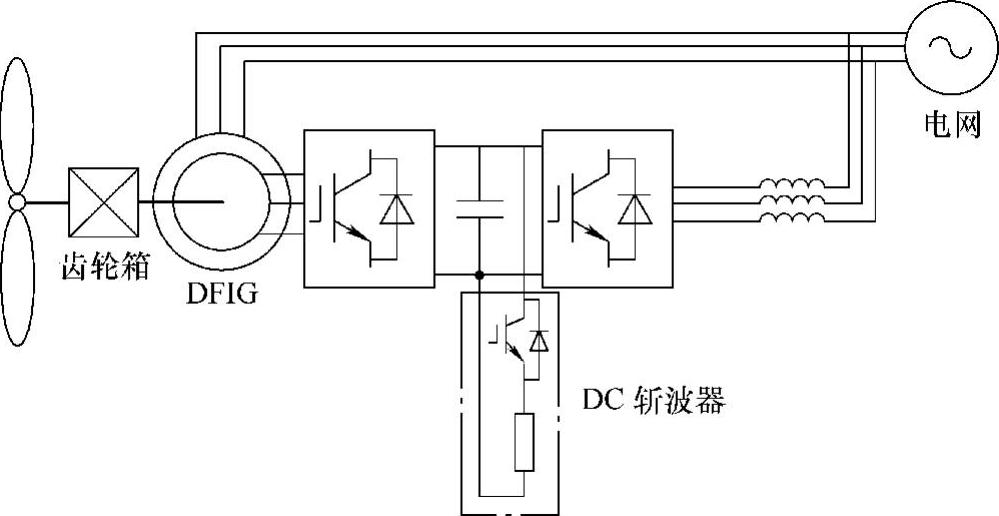
图6-28 直流母线并联斩波器电路(www.xing528.com)

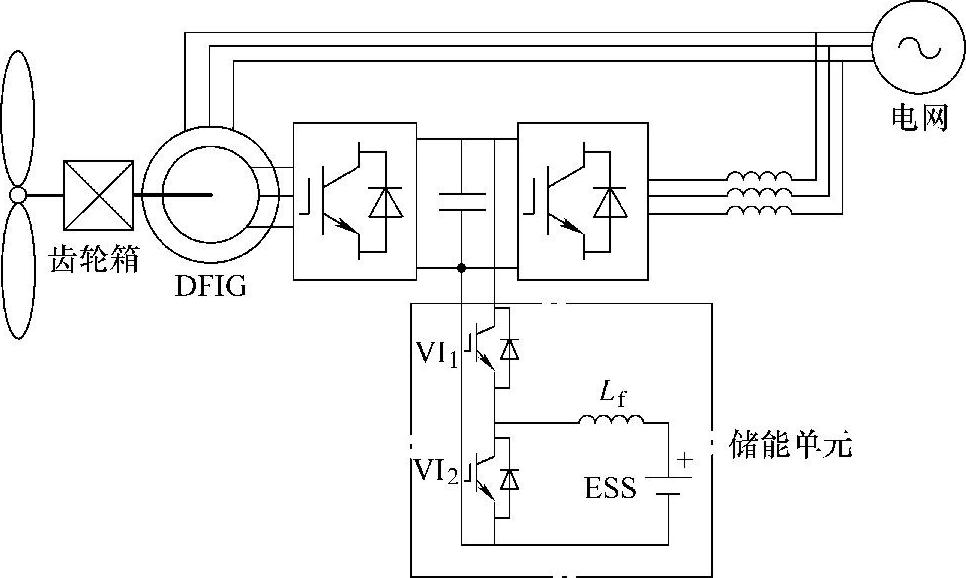
图6-29 直流母线并联储能装置

（3）定子侧串联SDBR

对于双馈型风电机组，同样也可以采用在定子侧加装串联动态制动电阻（SD-BR）的方式来提高机组在故障初始阶段的低电压穿越能力^[3-5]。低电压期间，SDBR的主要作用为：增大对定子磁链动态的阻尼，加快暂态直流分量的衰减，使机组尽快进入可控区；制动电阻上的压降可削弱机组定子端电压的跌落深度，还可消耗部分过剩能量、抑制风力机加速。

SDBR方法的典型拓扑如图6-31所示。电网正常时，旁路开关闭合，将制动电阻短路；检测到电网故障后，旁路开关断开，将制动电阻串入双馈发电机定子侧与电网之间，此时双馈发电机的定子等效电阻增大，等效的定子时间常数可类似式（6-9）表示为

通常，R_SDBR远大于R_s^[3]，故SDBR可有效减小定子时间常数，从而加快定子磁链暂态直流分量的衰减。关于SDBR削弱异步发电机定子端电压跌落深度的分析可参见6.2.2节，此处不再赘述。

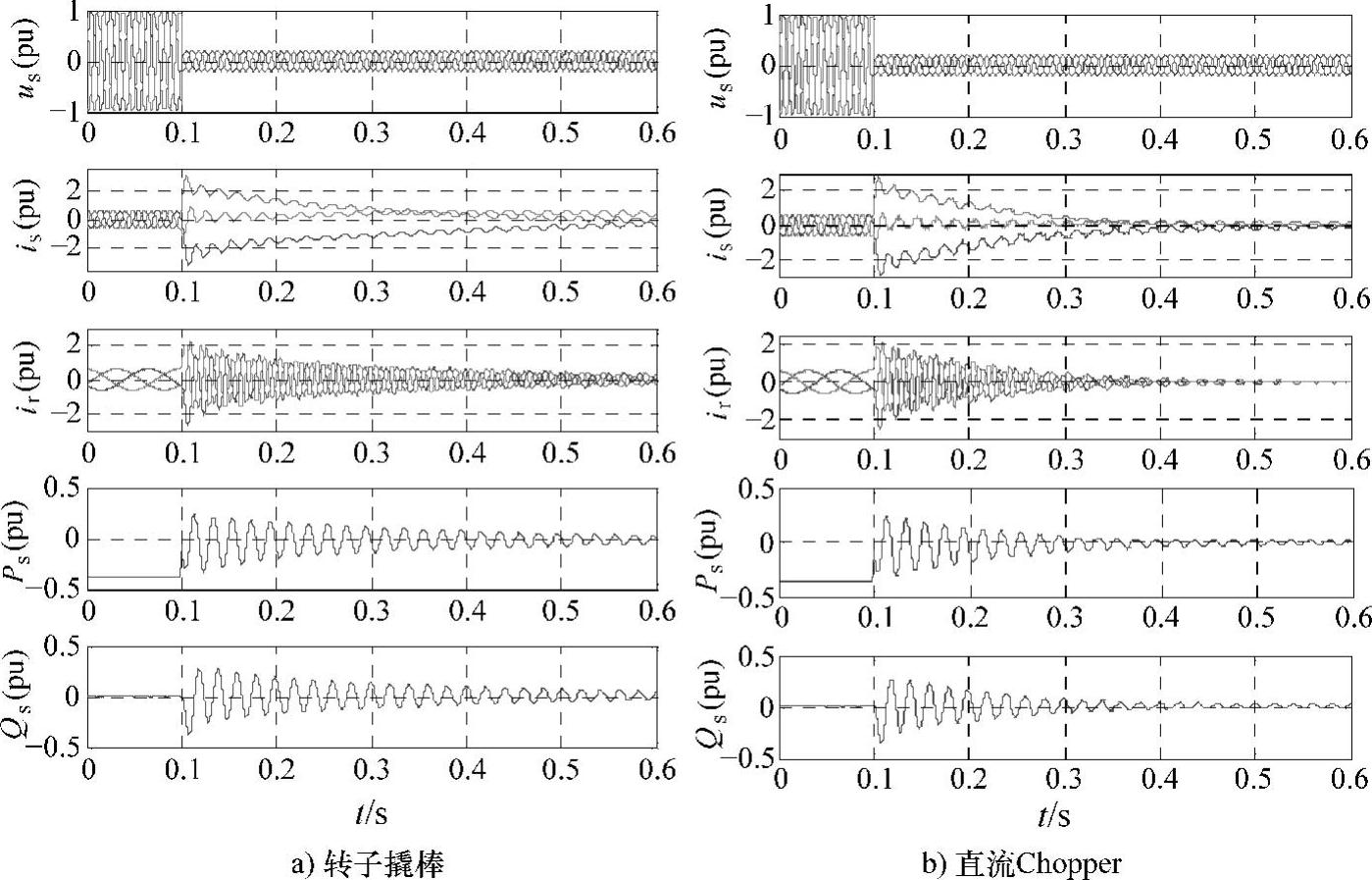
图6-30 三相对称故障（80%跌落深度）下分别采用转子和直流撬棒电路的仿真结果

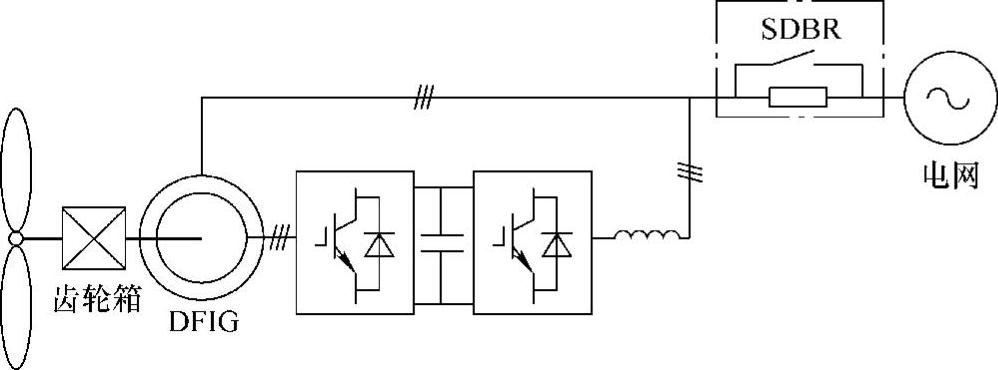
图6-31 定子侧串联SDBR的拓扑

在变速风电机组中，SDBR通常与机组变流器配合使用，通过两者的协调控制，有效地完成低电压穿越过程。在图6-31所示的双馈风电机组中，SDBR可与转子侧变流器、直流撬棒配合使用^[3]：电网故障后，将SDBR旁路开关断开，以接入制动电阻；同时，转子侧变流器切换至低电压穿越控制模式；暂态过程中，直流撬棒可维持直流母线电压。电网电压恢复后，闭合SDBR旁路开关，转子侧变流器恢复为正常控制模式。

以1.5MW双馈风电机组为例，通过仿真对比了定子串SDBR方法与转子撬棒方法，三相100%电压跌落故障下，仿真结果如图6-32所示。可见，采用转子撬棒方法时，转子过电流较大，定子磁链直流分量衰减较慢，且电磁转矩振荡剧烈。而采用SDBR方法时，故障期间双馈发电机转子电流可得到快速抑制，风电机组可保持并网运行状态，故障发生和恢复时刻，直流撬棒的动作时间较短；由定子磁链暂态响应可知，定子串SDBR方法可加快定子磁链直流分量的衰减，从而减缓并缩短双馈发电机在故障下的暂态过程，有助于满足低电压穿越导则第一阶段对暂态时间的要求；此外，该方法可有效抑制发电机电磁转矩振荡、延长机组寿命。

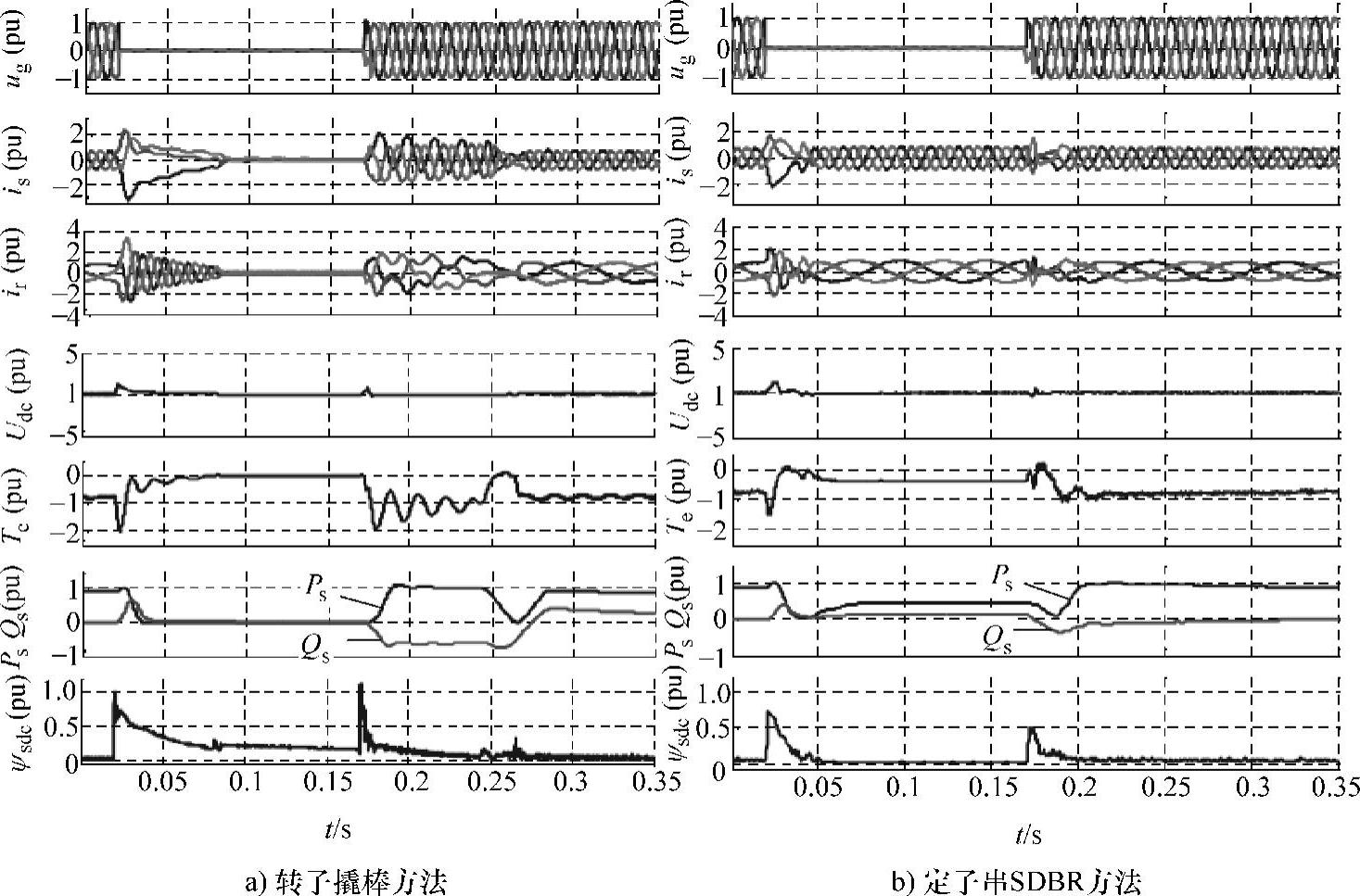
图6-32 对称全跌落故障下的仿真结果

SDBR阻值R_SDBR的选取会影响系统的控制性能。由式（6-49）可知，R_SDBR越大，定子磁链暂态直流分量的衰减越快，且可消耗的过剩能量越多。然而，R_SDBR增大会导致SDBR尺寸增加和成本上升，且过大的R_SDBR会降低系统的稳定性^[5]。因此，需要综合多方面的因素来设计R_SDBR阻值。

定子侧串联SDBR方法的优点是，通过与转子侧变流器的协调控制，可以有效抑制双馈发电机转子短路电流，并且缩短故障下的暂态过程，增加定子磁链阻尼，从而快速恢复机组的无功功率控制。但该方法增加了系统成本，且由于正常运行时需要旁路开关始终导通，该方法还增加了系统损耗。

值得注意的是，该方法既可基于单机系统实施，也可从风电场的层面，将该装置集中安装在整个风电场的并网点处，在辅助风电场内各风力机的低电压穿越的同时，降低装置的安装和维护成本。然而，由于其成本较高、效率较低，该方法在实际风电系统中并未得到应用。

（4）定子侧串联动态电压恢复器

在双馈发电机定子侧串联动态电压恢复器（Dynamic Voltage Restorer，DVR）可提高风电机组在三个故障阶段的低电压穿越能力，其基本工作原理是：电网故障后，在双馈发电机定子侧与电网之间串入DVR，以补偿故障引起的电压跌落、抑制双馈发电机定子磁链的负序和暂态直流分量，从而隔离电压跌落对转子回路的影响。其典型拓扑如图6-33所示。该方法既可基于单机系统实施，也可集中安装在整个风电场的并网点处，辅助风电场内各风电机组实现低电压穿越；然而，在风电场层面，该方法的应用前景并不乐观，其原因是：采用串联结构将改变电力系统的参数，这必须得到电网运营商的许可，而电力系统以安全运行作为最高准则，其运行策略相对保守，对此类改变通常并不支持；在单机层面，该方法似乎更有应用前景，因为单机设备可由风电场运营商自主决定。关于在风电场层面实施该方法的介绍将在本书第7章展开，本节将着重介绍如何在单机层面实现该方法。

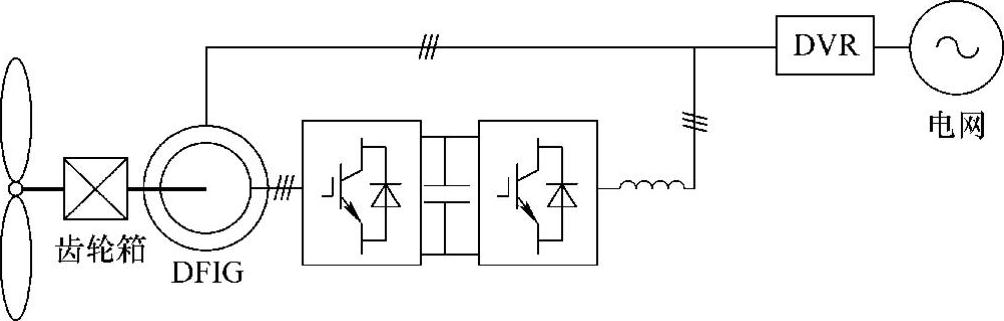
图6-33 定子侧串联DVR的系统结构

对于双馈单机风电系统，DVR可与转子背靠背变流器共用直流母线，以节省成本，此结构下，DVR也可称为定子侧的串联网侧变流器（Serial Grid Side Con-verter，SGSC），其典型拓扑如图6-34所示[39^-42]。图6-34a所示结构中，双馈发电机定子绕组从中性点处被打开，SGSC通过定子绕组连接到电网；图6-34b所示结构中，SGSC通过三相变压器串联到双馈发电机定子侧与电网之间。两种拓扑不同，本质却相同，均通过控制SGSC的输出电压来控制故障后双馈发电机的定子磁链，从而减弱故障对转子回路产生的影响。

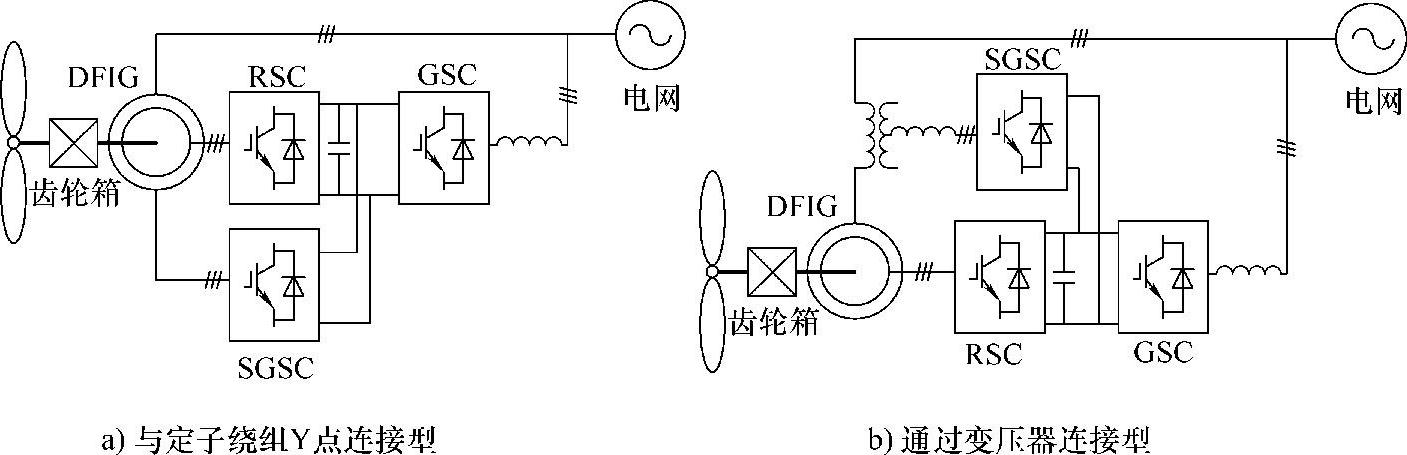
图6-34 定子侧串联网侧变流器的拓扑

下面以6-34b所示的结构为例，介绍不同故障下SGSC的控制策略。电网故障后，定子磁链负序和暂态直流分量是引起转子侧过电流的主要原因，控制SGSC输出电压，抑制双馈发电机定子磁链的负序和直流分量，则可有效抑制转子过电流[43]。

与式（6-30）类似，定义虚拟电网磁链为

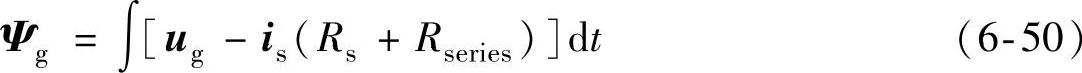
式中，R_series为SGSC串联变压器的等效电阻。电网故障后，Ψ_g可能含有正序、负序和直流分量，即Ψ_g=Ψ_g⁺+Ψ_g^-+Ψ_gdc。

由于SGSC的隔离作用，电网电压与双馈发电机定子端电压的关系为

u_g=u_s+u_SGSC （6-51）

将式（6-30）和式（6-51）代入式（6-50），可得

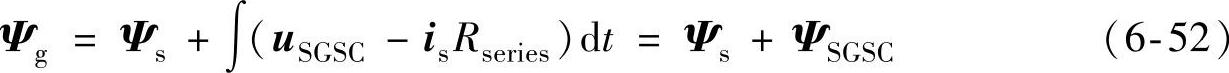
式中，Ψ_SGSC为SGSC输出虚拟磁链。

进一步，由式（6-52）可知，电网故障后，若控制SGSC的输出电压，使其虚拟磁链为

Ψ_SGSC=Ψ_g^-+Ψ_gdc （6-53）

则双馈发电机定子磁链仅含正序分量，直流和负序分量可被有效抑制，即

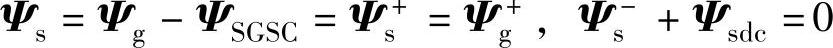
基于上述思想，SGSC的典型控制框图如图6-35所示，控制系统包括四部分：磁链指令计算、定子磁链观测、正序磁链分量控制、负序及暂态直流磁链分量控制。

图6-35中，定子磁链指令计算可在式（6-50）的基础上，采用图6-20所述方法分离得到，也可采用图6-35所示方法，Ψ_g经正序旋转变换后，含直流100Hz和50Hz波动分量（分别对应静止坐标系下的正序、负序和直流分量），采用100Hz及50Hz陷波器滤波后，即可得到正序分量，作为SGSC的正序虚拟磁链指令值；定子磁链观测可由式（6-30）得到，采用类似方法可计算定子磁链的正、负和零序分量反馈值。与式（6-50）类似，若忽略较小的SGSC并网电阻，SGSC的虚拟序磁链分量分别与其序电压分量呈积分关系，分别在正反向旋转坐标系下设计磁链闭环控制器，采用P调节器控制SGSC输出电压，可实现各序磁链的线性跟踪控制。由6.3.1节的分析可知，电网发生故障时定子磁链的直流分量和负序分量会在双馈发电机转子侧产生很大的反电动势，从而引起转子过电流。通过控制SGSC的输出电压，可以快速消除定子磁链的直流和负序分量，抑制定子磁链对转子回路的影响。在此基础上，双馈发电机转子侧和网侧变流器的控制算法可不做改动。

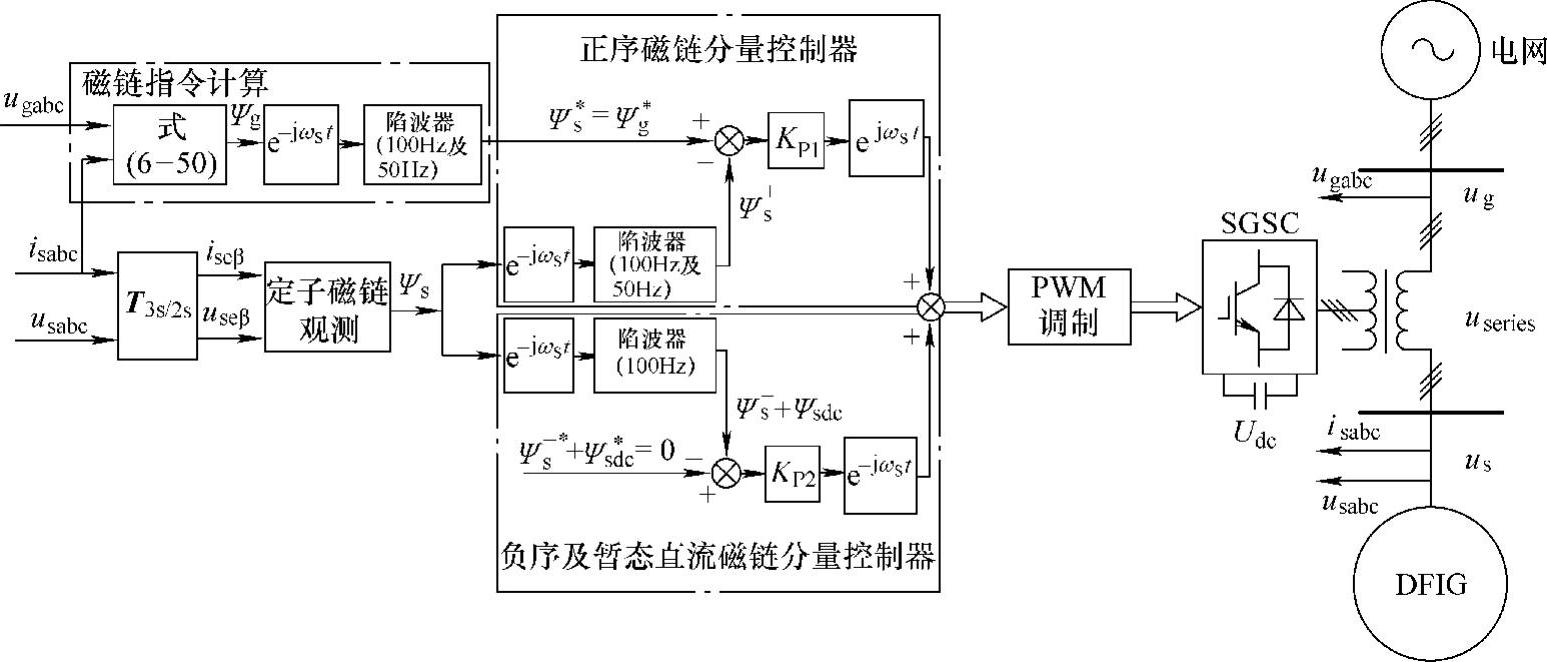
图6-35 SGSC典型控制框图

以1.5MW双馈风电机组为例，对串联网侧变流器的控制策略进行仿真验证。假设电网在3s时发生故障，3.15s时故障线路切除。故障前发电机以转差率s=-0.3、单位功率因数且满载运行。检测到故障发生后，双馈发电机的控制策略不变，只将其输出功率指令置零，SGSC则采用上述控制策略对定子磁链进行控制。故障恢复后，双馈发电机恢复故障前功率输出。三相对称故障和单相接地故障条件下，系统的动态响应如图6-36所示。

可见，电网故障后，SGSC输出电压使得双馈发电机定子侧电压变化过程较平缓，不对称故障下，SGSC还会对不平衡电压进行补偿，使双馈发电机定子端电压趋于平衡。从定子磁链各序分量的波形来看，正序分量变化平缓，直流分量和负序分量均得到有效的抑制。因而，SGSC可有效隔离电网故障对双馈发电机的影响，改善定转子过电流及直流母线过电压的运行风险，在不对称故障下，还可有效抑制发电机电磁转矩的波动。

需要指出的是，该方法也适用于低电压穿越的故障持续和恢复阶段。故障持续阶段，针对不对称故障，SGSC可补偿不平衡电压，使双馈发电机定子端电压平衡，从而抑制甚至消除负序电压对双馈发电机的影响。此时，双馈发电机的控制结构可不作改变，通过修改功率（电流）指令值，可实现对无功功率的控制要求。类似地，在故障恢复阶段，SGSC同样可有效隔离电网电压突变对发电机的负面影响。

定子侧串联DVR是一种非常有效的低电压穿越方法，可实现各种低电压条件（甚至零电压跌落）的穿越，然而，该方法需要增加额外的大容量变流器和串联变压器，成本较高；因而在实际风电系统中也未得到应用。

本节介绍了四种典型的增加硬件辅助装置的方法，用于双馈机组在深度故障下的低电压穿越。除了上述四种典型方案外，还有一些学者提出了其他增加硬件辅助装置的方案，如在转子回路中串联动态电阻^[44]等，感兴趣的读者可以阅读相关的文献，这里不再具体介绍。

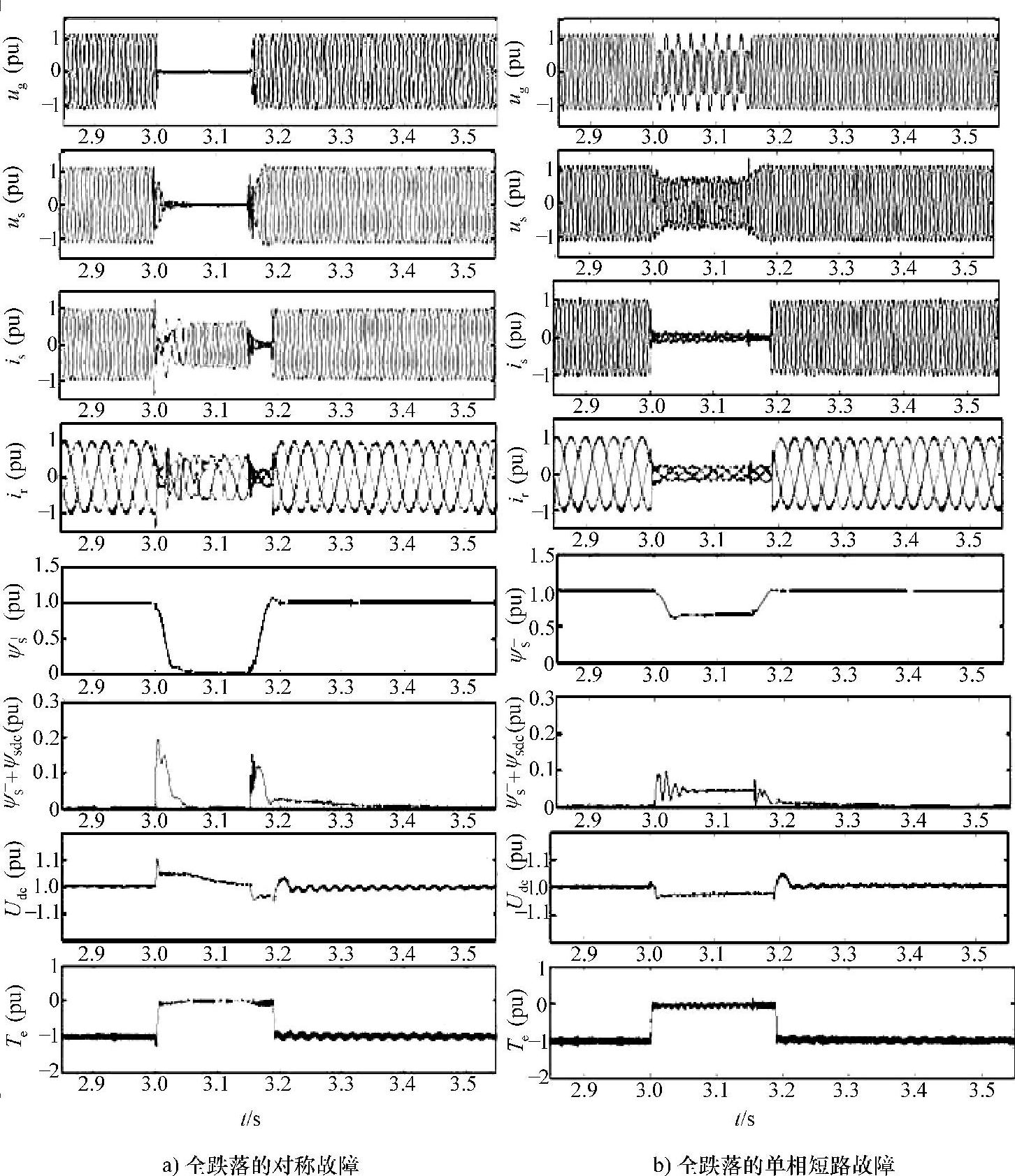
图6-36 SGSC控制实验结果

6.3.2.2 故障持续阶段的低电压穿越方法

在故障初始阶段，定子磁链的直流分量处于不断衰减过程中，到达故障持续阶段时，直流分量应基本衰减完毕。此时，双馈风电机组应处于可控状态，转子侧变流器需要根据并网导则的要求，控制双馈风电机组输出所需的有功或无功电流。对于对称故障，在正常运行所采用的控制策略（一般为传统的矢量控制方法，详见本书第3章）的基础上，只需修改电流环无功电流或有功电流的指令值即可满足并网导则的要求；对于不对称故障，由6.3.1节的分析可知，由于转子转差率的存在，定子电压的负序分量会在转子侧感应出较大的反电动势，考虑到转子变流器输出电压受其直流母线电压的限制，严重不对称故障条件下，转子侧负序电流难以受控，由于转子侧变流器输出电流的限制，双馈风电机组正序电流的控制能力也将受到影响^[18]。此外，定子电压和转子电流中负序分量的存在，会导致发电机电磁转矩和直流母线电压产生较大的两倍频波动，电磁转矩脉动过大会触发风电机组的振动保护，而直流母线电压波动会触发变流器的过电压或欠电压保护，这两种情况都会引起风电机组切机或脱网。因此，对于不对称故障而言，除了要满足并网导则的功率控制要求外，双馈风电机组还需要抑制发电机电磁转矩和直流母线电压的波动^[44]。可见，在故障持续阶段，对称故障的低电压穿越要求较容易满足，而不对称故障的控制则较困难。

1.不同故障下双馈风电机组的正序无功电流输出能力分析

现有并网导则大多针对对称故障而制定，从德国并网导则的发展及其已颁布的导则修订草案来看，未来导则将明确规定不对称故障下风电机组正序无功电流的控制要求，本节将针对双馈风电机组，定量讨论其正序无功电流的输出能力。

不平衡电网条件下，双馈风电机组的动态模型可由对称分量法分解为正序和负序模型^[45，46]，正负序模型分别经正序和负序同步旋转变换后，得到正负序旋转坐标下双馈风电机组的模型为

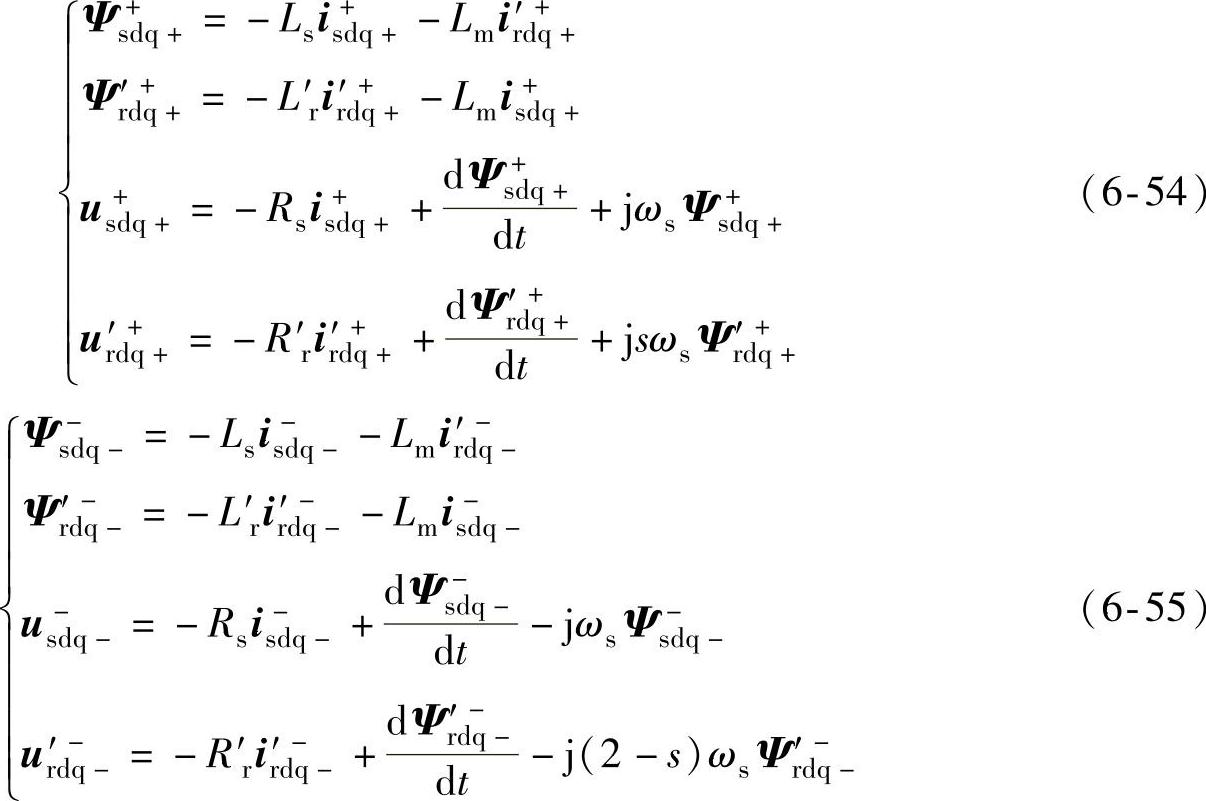
式中，F=F_d+jF_q（F=u，i，Ψ）；下角标+、-表示正、反向同步旋转坐标系；上角标+、-表示正、负序分量。

类似地，网侧变流器的动态模型也可分解为正序和负序模型，在正负序同步旋转坐标下，可表示为

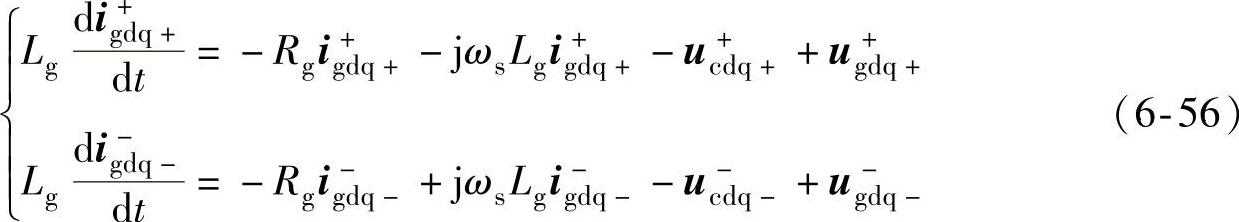
式中，L_g、R_g为网侧变流器并网电感和电阻；下标“c”表示网侧变流器的输出变量（并网电感前）；网侧变流器与双馈发电机定子端的并网点相同，因此有u_g⁺dq+=。

在正向同步旋转dq坐标系下，各物理量可以表示为

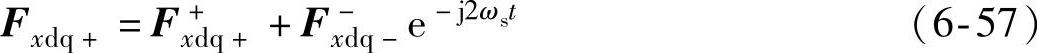
式中，x=s，r，g，c分别表示发电机定子侧、转子侧、网侧变流器电网侧和交流输出侧变量。则双馈风电机组定子侧和网侧变流器输出至电网的有功功率和无功功率为

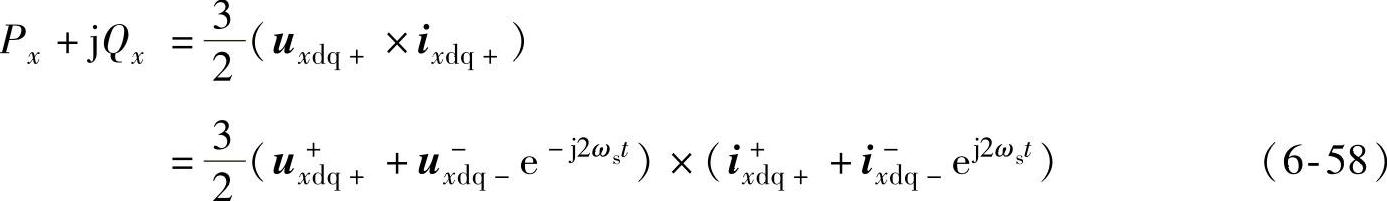
式中，“×”为矢量积符号，将式（6-58）中的电压和电流矢量按F_x=F_xd+jF_xq形式代入可得[47]

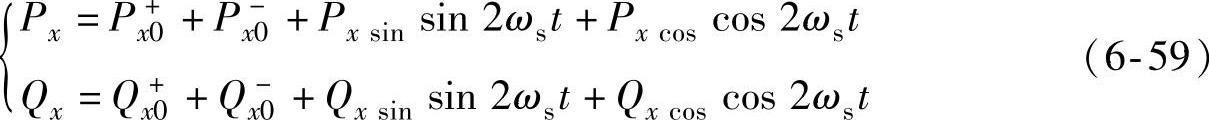
式中

双馈风电机组的输出电磁转矩可表示为

式中，P_e为电磁功率^[30]，有

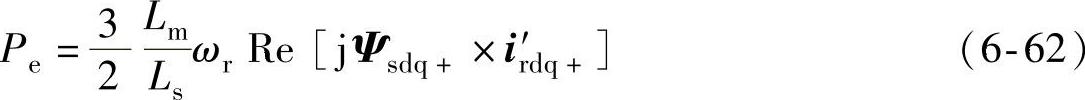
将式（6-62）代入式（6-61）可得

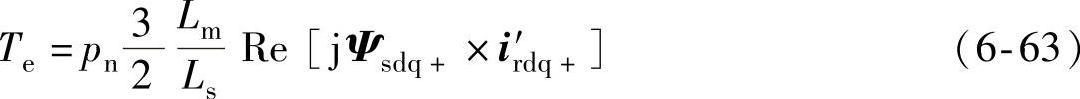
整理后可得

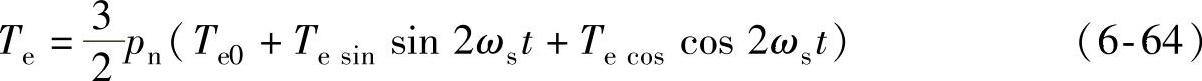
式中

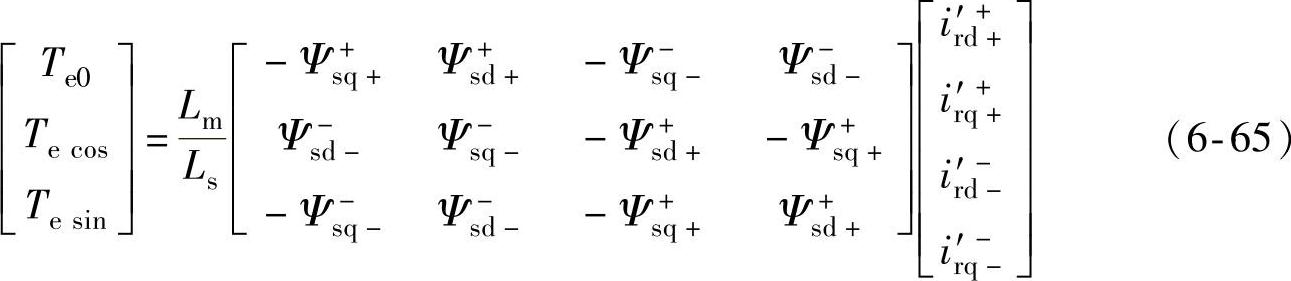
故障持续阶段，双馈风电机组处于可控区，已进入稳态，此条件下，由式（6-54）和式（6-55）可得以下稳态电压方程：

式中，u_s⁺_dq+，u_s^-_dq-可由锁相环节测量得到；u_r⁺_dq+和u_r^-_dq-由转子侧变流器输出，受直流母线电压的限制；i_r⁺_dq+和i_r^-_dq-受转子侧变流器最大输出电流的限制。

转子电压正负序分量的空间矢量关系如图6-37所示，正负序电压矢量之和即为转子总电压矢量。由于正负序矢量在空间上旋转方向不同，转子电压矢量幅值为时变量，当正负序矢量同方向时，矢量幅值达到最大；对于转子电流，也有同样结论成立。由以上分析可知，若要保证不平衡电网电压条件下双馈风电机组仍受控，转子电压（电流）的正负序矢量幅值之和必须在转子侧变流器的最大输出电压（电流）的范围之内，即

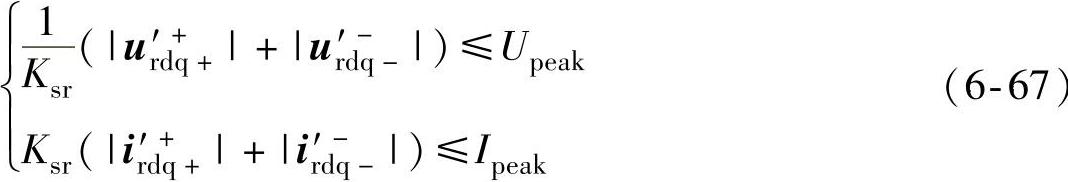
式中，U_peak、I_peak为转子侧变流器输出电压和电流的最大值，分别受直流母线电压和变流器输出额定电流的限制。通常，U_peak=（1.1～1.2）pu，I_peak=（0.4～0.5）pu（以定子额定参数为基准值）。需要注意的是，实际双馈风电机组中，转子侧变流器的设计容量往往大于网侧变流器。正常运行时，电网电压恒定（即为发电机定子侧额定电压），同样以定子额定参数为基准值，网侧变流器容量可设计为（1/4～1/3）pu，则其额定电流也为（1/4～1/3）pu。然而，由于双馈风电机组转差率可变，其转子侧电压在运行中会发生变化，发电机运行在最大转速时，对应的转子侧电压达到最大，但此时转子电流往往并非最大；反之，转子电流达到最大值时，转子侧电压未必为最大值。考虑到实际电力电子器件的过载能力有限，系统正常运行时，转子侧变流器必须同时能够承受最大电流和最大电压，因此转子侧变流器容量一般设计为（0.4～0.5）pu，而非理论上的（1/4～1/3）pu，高于网侧变流器，转子侧变流器可输出的最大电流也相应为（0.4～0.5）pu。式（6-67）中，K_sr为定转子绕组匝数比，对于双馈风电机组，其值通常在0.3～0.4之间。由于式（6-66）中转子侧变量都已经过绕组折算到了定子侧，而U_peak、I_peak为实际参数的限制值，因而式（6-67）中的电压电流变量须经过绕组反折算。

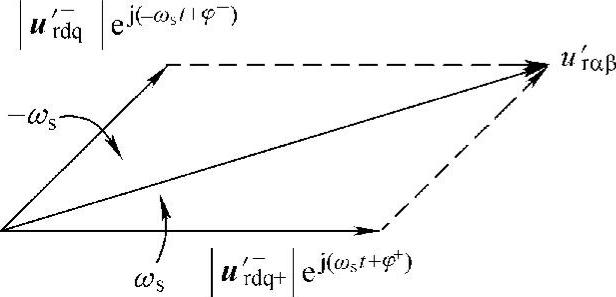
图6-37 转子电压正负序分量的空间矢量

双馈风电机组定子侧输出的正序无功电流矢量与正序电压矢量垂直，其最大值可表示为

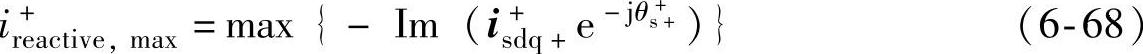
式中，θ_s⁺₊为正序定子电压矢量与正序旋转坐标系d轴的夹角。

若已知故障后定子正负序电压分量，则双馈风电机组定子侧所能输出的最大正序无功电流可由式（6-66）～式（6-68）求得。式（6-66）～式（6-68）所描述的问题为具有非线性约束的最优化问题，其求解详见本书附录D。

由第5章的电网故障特性分析可知，在新能源发电系统的典型并网结构下，故障点电压的正负序分量可以表示为相对故障距离λ和阻抗角α的函数，而已知故障点正负序电压分量，则可由式（6-66）～式（6-68）可求得双馈风电机组所能输出的最大正序无功电流i_r⁺_{eactive，max}。以λ，α为变量，i_r⁺_{eactive，max}为输出量，可得到图6-38所示的一族曲线。

根据6-38的结果，可得到以下结论：

1）如果故障很轻（故障点距离GCP点较远），双馈发电机定子侧可输出最大正序无功电流可达其最大值，以本章所采用的双馈风电机组参数为例，其值大约为0.83pu（与参考文献[48]中所得极值相同）。需要指出的是，通常商业化双馈发电机定子侧输出额定功率并不按照1pu来设计，因其转子所连背靠背变流器还可将部分功率馈入电网，定子与转子输出额定功率之和大约为1pu。

2）对于三相故障，双馈发电机始终可控，即使故障发生在GCP处也不例外，且故障点越靠近GCP，ir+eactive，max会越大，可见对称故障条件下，双馈风电机组较容易满足并网导则的无功功率输出要求。对于不对称故障，故障点距离GCP越近，正序无功电流的输出能力越小，λ较小时，ir+eactive，max甚至为负数，表示此时双馈风电机组必须吸收部分正序无功电流才能保持并网运行，若考虑并网导则的要求，可认为严重不对称故障下，风电机组存在不可穿越区。此外，三种不对称故障类型中，相间短路故障的不可穿越区最大；相同λ下，相间短路故障的ir+eactive，max也最小。因而，对于双馈风电机组而言，相间短路故障的低压穿越最为困难。相比于相间对地短路故障，单相故障更为严重，相同故障距离下，风电机组所能输出的最大正序无功电流也较小，其原因可结合图5-10分析：两种故障条件下，电网电压中的负序分量相同，而相间对地短路故障下电网电压正序分量更小，其在转子绕组上感应的电动势正序分量也较小，此时，转子侧变流器只需要输出较小的正序电压即可抵消此反电动势的影响，与单相接地故障相比，转子侧变流器输出控制电压的裕量更大，因而风电机组所能输出的正序无功电流也更大。

3）阻抗角α的大小会影响双馈风电机组的低电压穿越能力，但并不明显。对于三相对称故障，α越小，传输线的等效电容越大，由于等效电容可提供部分无功补偿，相同故障点下，α越小，故障点电压跌落越小，双馈风电机组可输出的ir+eactive，max也越小。对于不对称故障，α减小会导致负序电压分量增大，由于负序电压分量对双馈风电机组的影响比正序电压分量大，则低电压穿越难度增加，从图6-38可见，随着α的减小，故障不可穿越区增大。

4）转差率s的大小会影响双馈风电机组的低电压穿越能力。转差率|s|越大，不对称故障下双馈风电机组的不可穿越区越大，其原因是：为使得双馈发电机有效受控，且输出正序无功电流最大，转子侧感应电动势的负序分量需部分降落在转子侧阻抗上（对于负序分量，因频率较高，转子侧感抗值也较大，因而负序电压导致的负序电流不会太大），转子侧变流器需输出足够的正序分量以抵消其正序感应电动势，并控制正序无功电流，由于正序感应电动势幅值与|s|成正比，|s|越大，双馈发电机受控所需转子侧变流器输出电压越高，输出最大正序无功电流越小；相同故障条件下，与次同步速运行时相比，运行在超同步速下双馈风电机组的低电压穿越更困难，因为此时转子侧感应电动势的负序分量更大。

进一步，若增大转子侧变流器容量，双馈风电机组定子侧输出最大正序无功电流曲线如图6-39所示。可见，增大转子侧变流器容量可有效减小故障不可穿越区，当容量增大到0.6pu时，不可穿越区消失（λ=0时，双馈风电机组定子侧可输出0.2pu的正序无功电流，考虑到其网侧变流器还能输出0.2pu的正序无功电流，德国SDLWindV并网导则草案的规定可得到满足），此时，定子所能输出的最大正序无功电流甚至可以超过其额定值（0.83pu）。由于正序无功电流输出的要求仅发生在电网故障的短时间内，双馈发电机定子的短时过载运行是可以被允许的。

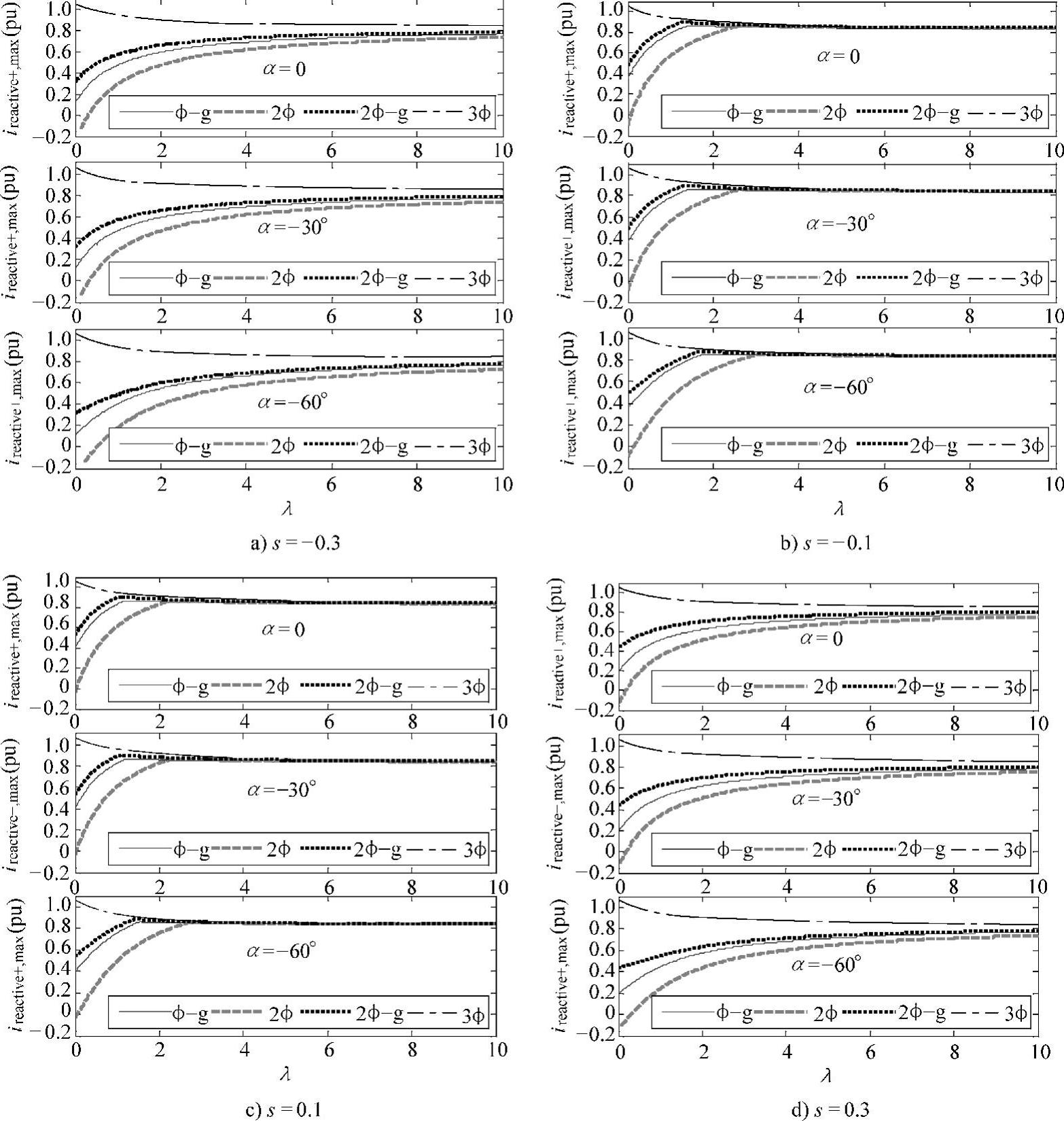
图6-38 不同故障下的双馈发电机定子侧能够产生的最大正序无功电流（I_peak=0.4pu）

由以上分析可知，在低电压穿越的第二阶段，若转子侧变流器容量较小（0.4pu），为满足并网导则，需要增加额外的无功补偿设备，以辅助双馈机组的低电压穿越；若增大转子侧变流器容量，双馈风电机组可以成功穿越所有的故障类型。然而，严重故障条件下，双馈发电机的正序无功电流输出能力有限。

需要注意的是，上述结论并未考虑电力系统传输线和升压变压器阻抗对发电机机端电压的影响，因而结论偏保守。尽管如此，上述结论在实际应用中仍有一定的价值，例如，由于严重不对称故障下，双馈风电机组的正序无功电流输出能力有限，双馈风电场有必要配备一定容量的无功设备，如STATCOM或SVC等，以辅助其完成低电压穿越；极限情况下，德国SDLWindV并网导则草案的要求无法满足，若考虑传输线和升压变压器阻抗的影响，该草案有一定的合理性。此外，对于实际拟建双馈风电场，若传输线和升压变压器阻抗已知，采用上述分析方法可得到双馈风场输出正序无功电流能力的准确结果，为风电场的无功配备提供参考。

2.对称故障下双馈风电机组的低电压穿越

对于对称故障，在正常运行所采用的控制策略的基础上（一般为传统的矢量控制方法，详见本书第3章），当检测到电网故障后，只需根据并网导则的要求修改电流环无功或有功电流指令值即可，此处不再赘述。

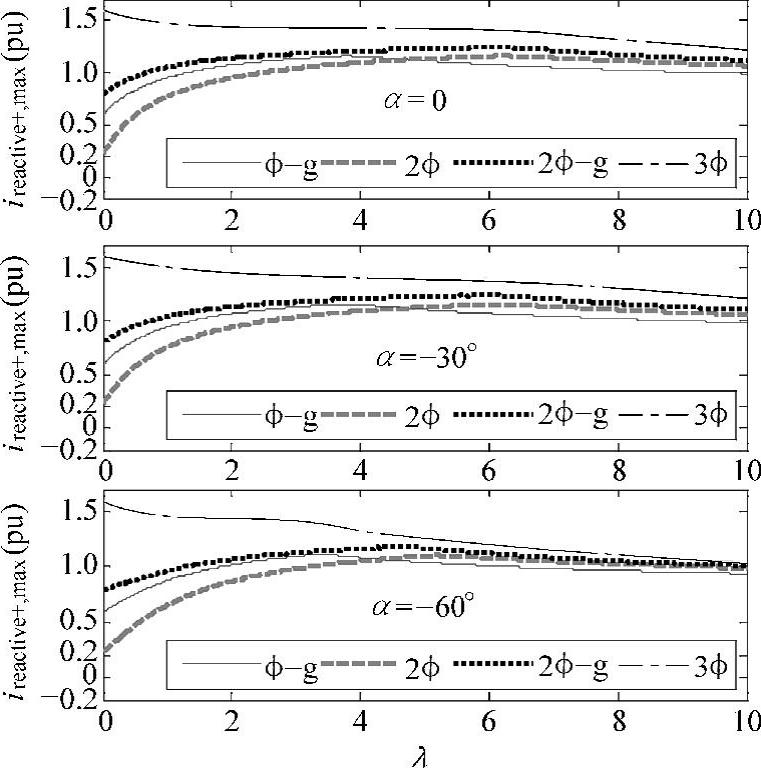
图6-39 转子侧变流器容量对双馈发电机输出最大 正序无功电流的影响（s=-0.3，I_peak=0.6pu）

3.不对称故障下双馈风电机组的低电压穿越

不对称故障下的双馈风电机组控制目标由并网导则要求决定。下面以德国SDLWindV并网导则草案的要求作为控制目标展开讨论（即故障下双馈风电机组要保证具有0.4pu正序无功电流的输出能力）。此外，为防止不对称电压下发电机电磁转矩和直流母线电压波动所引起的切机现象，控制目标还需要考虑抑制上述波动。综合以上考虑，控制目标可由以下各式表示：

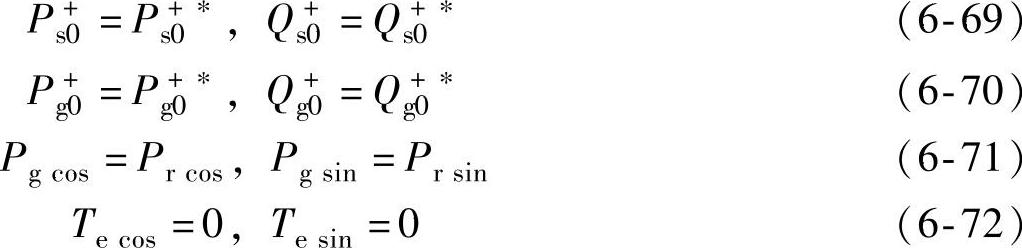
式中，P_s+₀^∗为定子正序有功功率指令，其值由具体的并网导则决定，如爱尔兰的WFPS1并网导则对故障后风电系统的有功输出作了相应规定；Q_s+₀∗为定子侧正序无功功率指令，几乎所有的并网导则都对此有相关要求；P_g+₀∗为网侧变流器的正序有功功率指令，其值一般为直流母线电压外环控制器的输出；Q_g+₀∗为网侧变流器的正序无功功率指令，电网电压正常时，Q_g+₀∗一般为零，此时网侧变流器工作在功率因数为1的状态，故障时设定Q_g+₀∗值可使网侧变流器为电网提供无功电流支撑。与Q_g+₀∗的控制相比，变流器直流母线电压的控制（即P_g+₀∗的调节）更为重要，Q_g+₀∗的最大值一般由P_g+₀∗和网侧变流器的额定电流共同决定。式（6-71）和式（6-72）可消除发电机电磁转矩和变流器直流母线电压的脉动。需要注意的是，由于转子侧变流器控制能力的限制，上述控制目标并不一定能同时实现，因此在上述控制目标的基础上，还需要定义控制优先级。从电网角度来看，满足并网导则是至关重要的，因其关系到电力系统的稳定运行；相比较而言，在故障过程的短时间内，只要不超过限定值，发电机转矩和变流器直流母线电压的脉动是可以被容忍的。因而，故障后转子侧变流器可优先控制P_s+₀∗和Q_s+₀∗，以满足并网导则的要求，在此基础上，其剩余容量用以抑制发电机转矩脉动；相似地，网侧变流器则优先控制P_g+₀∗和Q_g+₀∗，剩余容量用以抑制直流母线电压脉动。上述控制优先级可通过控制器中限幅环节的设计来保证。

严格来讲，式（6-71）并不能准确地消除变流器直流母线电压的脉动[49]。其原因是，消除直流母线电压脉动必须保证转子侧变流器输入功率的脉动可被网侧变流器完全送出；然而，上述分析中，P_g为网侧变流器输出到电网的功率，并非网侧变流器交流侧的输出功率，分析中忽略了网侧变流器输入电感上的功率波动。若要实现直流母线电压的高精度控制，需要进一步考虑并网电感上的功率波动，对式（6-71）进行修正^[49]。上述影响和控制算法的修正在本节分析中将不作考虑，其原因是电网故障较轻时，并网电感上的功率波动也较小，对控制精度影响并不大，电网故障较重时，网侧变流器应优先控制P_g+₀∗和Q_g+₀∗，抑制直流母线电压波动的需求次之。

若定义正序旋转坐标系的d+轴与正序电压矢量重合（正序电压定向），则us+q+=0，系统模型式（6-54）、式（6-55）、式（6-59）、式（6-60）及式（6-64）、式（6-65）可进一步被化简，在此基础上的控制器设计也可简化。考虑简化后的系统模型及控制目标式（6-69）～式（6-72），可得转子侧和网侧变流器的输出电流指令为[18]

式中，；；。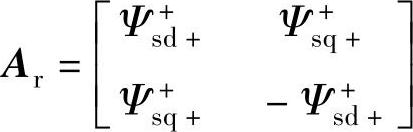

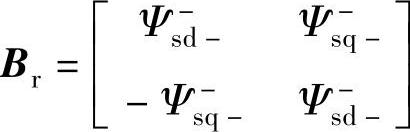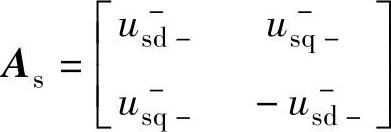综上所述，可得到转子侧和网侧变流器的控制框图如图6-40所示，图中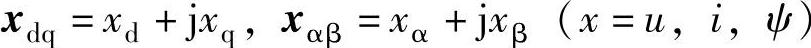，；定转子电压、电流和磁链正负序分量的分离算法可采用第5.2节所述的基于旋转或静止坐标系下的锁相环得到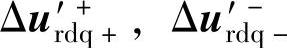；为前馈解耦项，其目的是为了抵消系统模型中的交叉耦合项，使控制电压分别与电流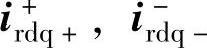呈线性关系，实现正负序电流的解耦控制，其值可由式（6-54）、式（6-55）计算得到，即

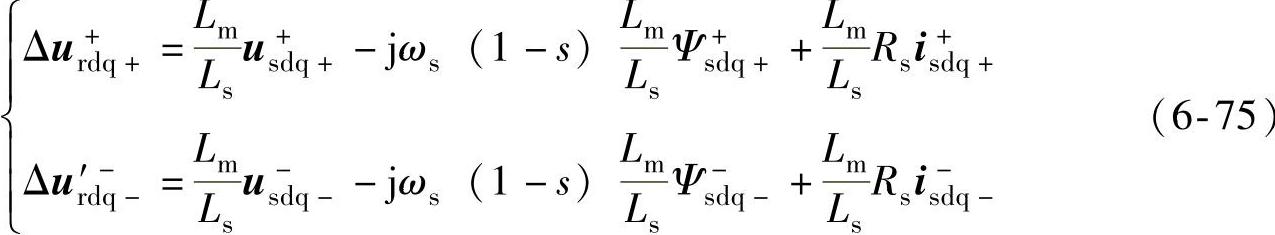
为保证控制优先级，图6-40中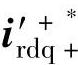，和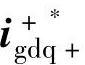为优先满足的控制目标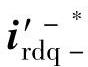，和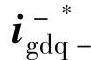则由变流器的剩余容量决定，可通过对变流器的正负序电压指令设置不同的限幅值而实现，如图6-40所示，负序电压限幅值由变流器输出电压矢量幅值和正序电压指令值共同决定，这使得正序电流分量的控制具有更高的优先级。

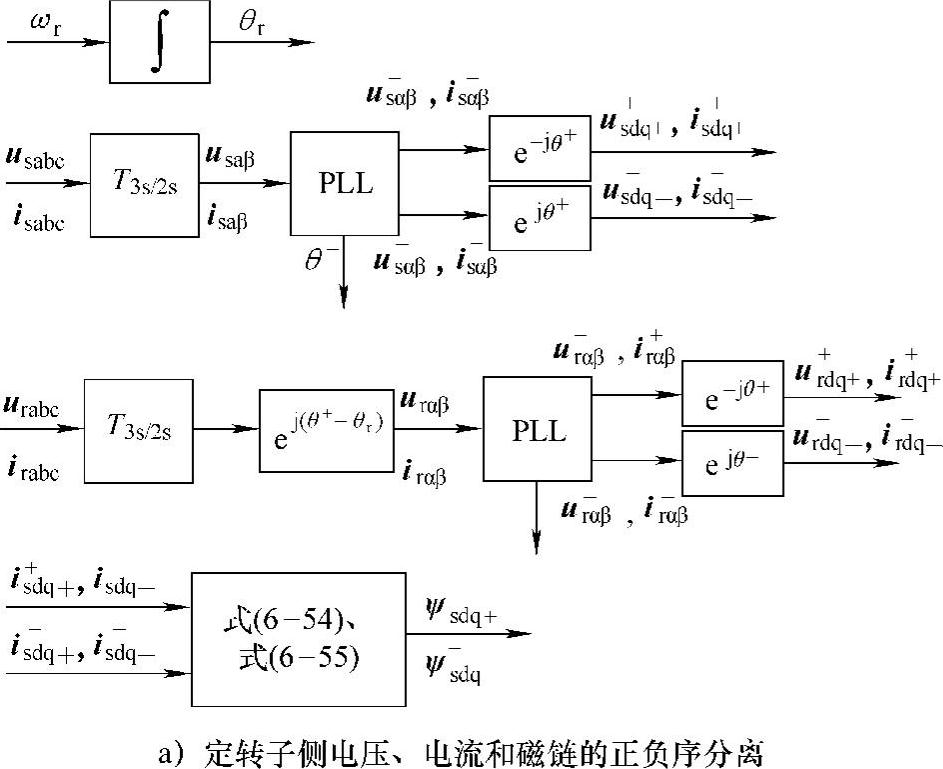
图6-40 考虑并网导则要求的不对称故障低电压穿越控制策略框图

在较轻的单相接地故障，对应0.083pu）下，采用该控制策略的仿真结果如图6-41所示。由图6-41a可知，故障后正负序电压跌落并未如前面分析结果那样严重，这是由于前面分析中忽略了线路和变压器阻抗，其结果相对保守，上述现象在弱电网结构下将更为明显（此时，忽略线路阻抗将引起更大的分析误差）。由于正序电压跌落幅值小于0.1pu，根据并网导则的要求，双馈风电机组无需发出正序无功电流。发电机定子侧输出有功功率和无功功率存在小幅波动，这是由受控的定子负序电流所造成的。转子侧电气变量的响应如图6-41b和c所示。由图6-41b可知，故障前转子电压频率为转差频率|s|ω_s/（2π）=12Hz，故障后，由于负序分量的存在，转子电压中出现11次谐波，其频率为|2-s|ω_s/（2π）=132Hz。由于定子电压负序分量较小，转子变流器控制能力足够，由图6-41c可知，转子电流的正负序分量都可受控，且较快地跟踪指令信号，最终发电机电磁转矩脉动被消除。采用上述方法，网侧变流器的控制可消除直流母线电压脉动，但因此其输出有功电流和无功电流中包含负序分量，为容忍此电流脉动，网侧变流器的容量需适当增加。故障运行前后发电机转差率s<0，发电机工作在超同步转速，有功功率从转子经背靠背变流器输出到电网。图6-41c中，发电机的各序电流分量都处于受控状态，然而正负序电流的控制代价明显不同，故障前后，用于控制正序电流的正序电压幅值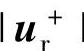变化不大，而为控制较小的负序电流，所需的负序电压幅值|ur-|高达0.4pu。由于故障较浅，故障初始阶段直流撬棒电路未启用。

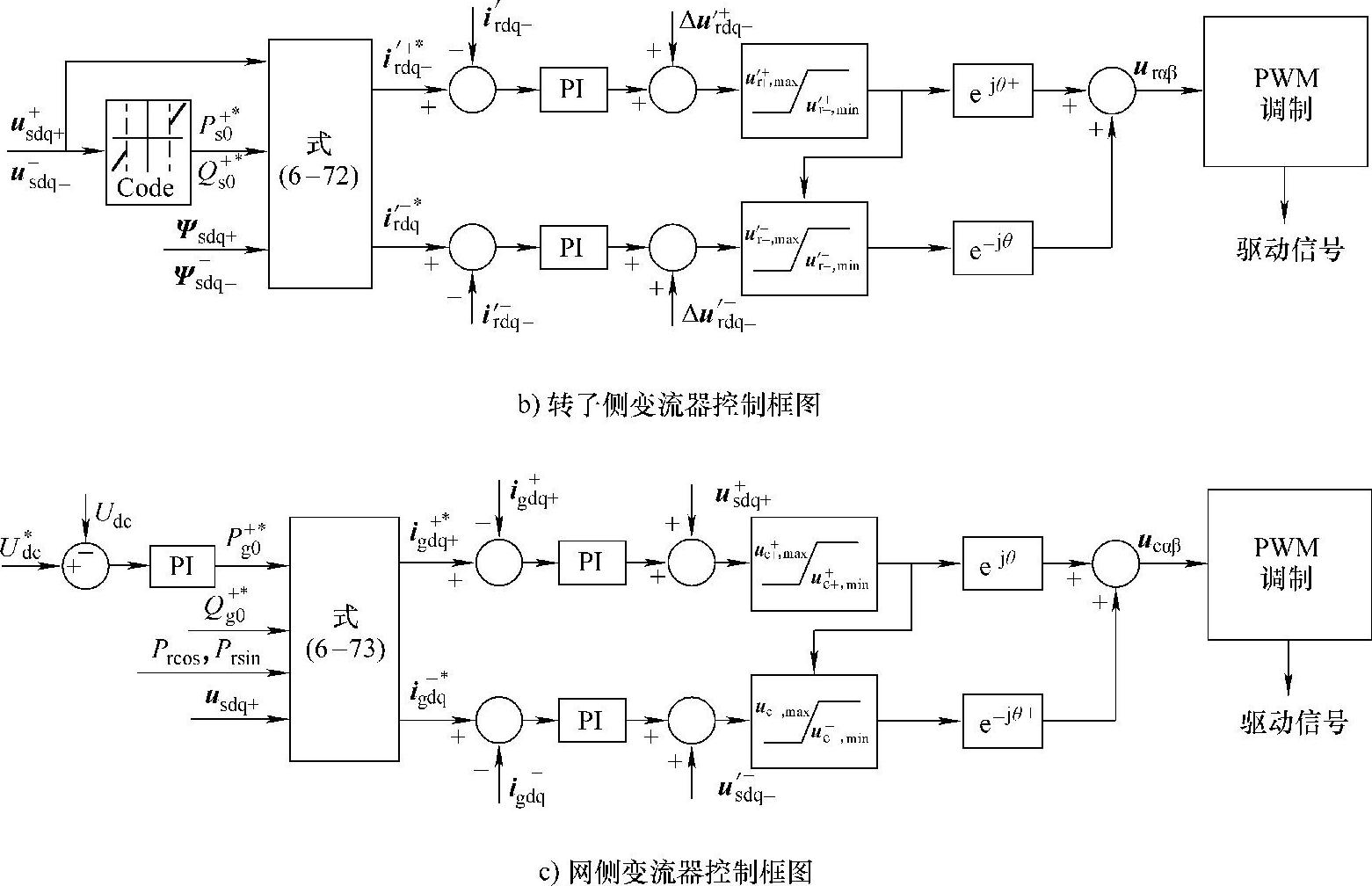
图6-40 考虑并网导则要求的不对称故障低电压穿越控制策略框图（续）

在较严重的相间短路故障（λ=1，α=0°，对应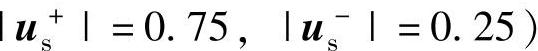下，采用该控制策略的仿真结果如图6-42所示。类似地，由图6-42a可知，故障后正负序电压跌落并未如前面分析结果那样严重；与图6-41a相比，正序电压跌落的仿真值和分析值之间的差距更大，这是由于此故障下正序电压跌落大于10%，根据并网导则的要求，发电机组需要输出正序无功电流以支撑电网，而正序无功电流可减小正序电压的跌落程度。同样，定子侧输出负序电流也可减轻电网的不平衡度，因而图6-42a中的负序电压分量也小于理论分析值。由于负序电流的存在，定

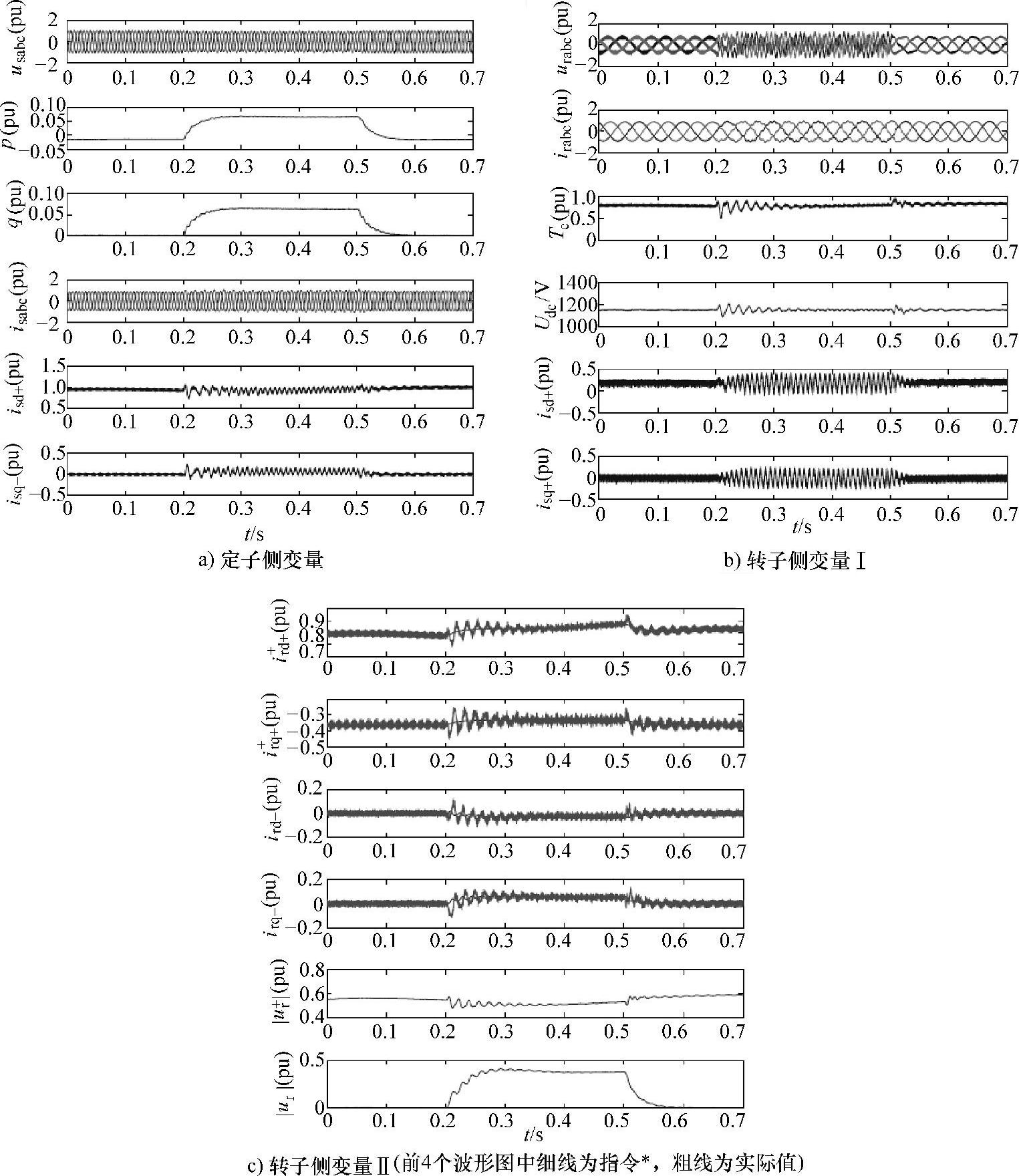
图6-41 较轻单相接地故障条件下低电压穿越策略仿真结果

子侧有功和无功电流分量存在振荡，与图6-41a相比，该振荡更为明显。定子侧无功电流的平均值，即正序无功电流，约为0.3pu，考虑到网侧变流器输出的平均无功电流（最大可输出约0.2pu），系统输出可以满足德国SDLWindV并网导则草案的相关规定。

转子侧电气变量响应如图6-42b和c所示。由图6-42b可知，转子电压中谐波（对应负序分量）较大，变流器输出已饱和。由于转子侧变流器控制能力有限，转子电流负序分量无法完全受控，因而故障期间发电机转矩脉动无法被消除。对于网侧变流器，其正负序电流的控制能力相同，负序电流始终受控，因而直流母线电压脉动仍可被消除。故障期间，网侧变流器输出的正序无功电流约为0.1pu。由图6-42c可知，转子电流的正序分量可以受控，但其负序分量无法跟踪指令值。故障前后，用于控制正序电流的正序电压幅值|u_r+|变化不大，约为0.6pu；转子侧变流器的剩余容量被用于输出负序电压（|u_r-|的幅值约为0.5pu），以抑制转矩和直流母线电压的脉动。由于故障较严重，故障初始和恢复阶段，转子绕组反电动势初始值较大，转子变流器无法受控，此时，直流撬棒电路动作，其开关管控制脉冲波形如图6-43所示。

事实上，当电网故障较轻时，转子侧变流器的控制能力足够，可实现的控制目标也较为灵活^[46]，根据不同的控制目标，计算所需的转子电流正负序分量，作为转子电流内环的给定值，还可实现其他目标，如消除定子侧瞬时有功功率的两倍频波动、转子电流或定子电流的负序分量等。当电网故障较重时，转子侧变流器的控制能力（尤其是对转子电流负序分量的控制能力）受限，上述目标则无法完全实现。此外，从电网稳定运行的角度来看，上述目标并未考虑实际电网的运行需求，因而其应用有一定的局限性。

除了改进变流器算法外，增加额外硬件设备（如DVR、STATCOM），也可实现双馈风电机组在故障持续期间的低电压穿越。采用DVR的方法在故障初始阶段已作详细介绍，用于故障持续阶段时，需要进一步考虑导则对正序无功电流的输出要求，该无功电流可由双馈风电机组输出，在前面所述方法基础上，根据检测的电网电压信息，进一步设定双馈风电机组的电流指令即可；采用STATCOM的方法用于单机和用于风电场并无太大差异，将在本书第7章中进行介绍。由双馈风电机组正序无功电流输出能力的分析可知，适当提高转子侧变流器的容量，通过改进风电机组的控制方法即可满足并网导则的要求，与增加DVR、STATCOM方案相比，该方案在成本和可行性方面似乎具有更大优势，事实上，为了通过低电压穿越检验，一些风力机变流器厂商在设计其产品时，都已增加了转子侧变流器的容量。

6.3.2.3 故障恢复阶段的低电压穿越方法

故障恢复阶段是指从电网电压恢复开始到其过渡过程结束的阶段，此阶段，因发电机输出有功功率和无功功率可独立受控，并网导则规定的功率恢复要求较容易得到满足。然而，故障切除时会出现电压幅值的骤升，将影响风电系统的安全运行。一方面，并网导则要求风电场在故障持续阶段输出一定的无功电流以支撑电网，当电网故障切除时，因为检测或控制延时，风电场的无功输出不可能立即停止，无功功率的过补偿往往会引起电网过电压；另一方面，故障持续期间风电场并

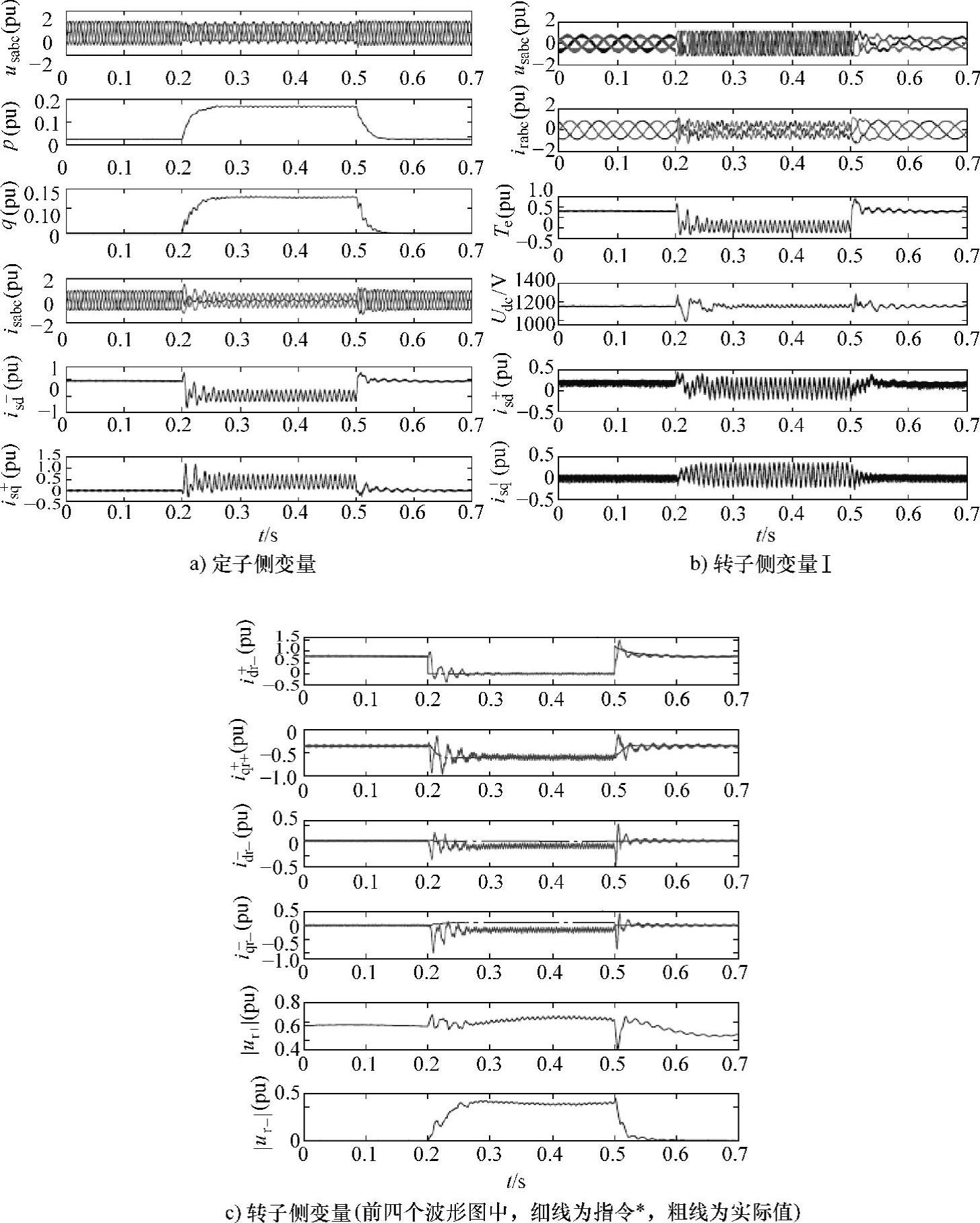
图6-42 严重相间短路不同故障条件下低电压穿越策略仿真结果

网处的带分接头的变压器往往会动作，以抬高风电场并网点电压，而故障切除后，带分接头的变压器动作的延时也将导致过电压。上述过电压现象不仅表现在幅值骤升上，还可能伴随着相位跳变，发电机转子反电动势也将因此而突增，这会导致转子过电流，威胁转子侧变流器的安全运行。

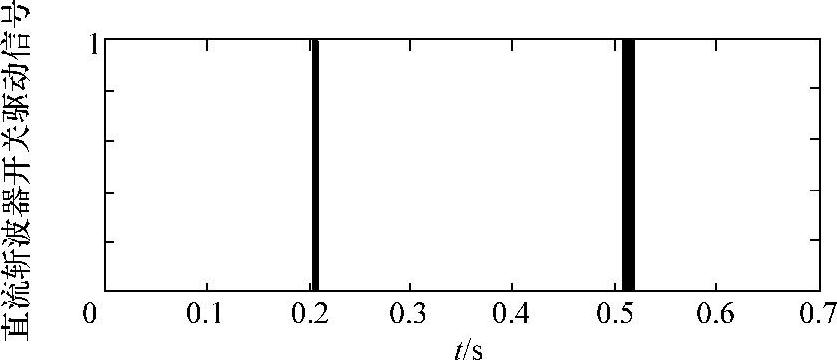
图6-43 直流撬棒动作信号

故障恢复阶段，过电压过程对发电机定子磁链和转子侧反电动势的影响与故障初始阶段的机理相似，具体分析可参考6.3.1.1节与6.3.1.2节的相关内容。值得注意的是，故障恢复阶段的过电压过程包括以下两个阶段：

（1）电网电压由跌落到过电压的跳变阶段

此阶段，电网电压跌落与过电压的影响叠加在发电机定子端，发电机定转子参数的过渡过程会比故障初始阶段更为剧烈；

（2）持续过电压阶段

此阶段，电网电压持续超过其额定值，严重时，发电机转子侧变流器无法受控。

与故障初始阶段相似，转子侧变流器的控制极限也可基于最优化理论进行分析，前面所述的故障初始阶段低电压穿越方法也均可应用于故障恢复阶段。若过电压程度较浅，可控制发电机和网侧变流器吸收一定的无功功率，以辅助电网电压恢复；若过电压程度较深，则发电机转子侧变流器将无法受控，此时需要接入额外的辅助设备，如转子撬棒，以抑制转子电流，接入撬棒时，双馈发电机工作在异步发电状态，吸收一定的无功功率，将有利于电网电压的恢复；此时，为避免过电流损坏，网侧变流器应处于关闭状态。

综上分析，故障恢复阶段的难点是高电压穿越（HVRT）问题，由于过电压对风电系统的影响及其故障穿越方法与故障初始阶段相似，本书对此内容将不做重点介绍，有兴趣的读者可阅读参考文献^[50-53]。