低电压故障对双馈风电机组的影响

在定子静止坐标系下，双馈发电机的帕克模型可表示为[16]

式中，u、i，Ψ分别为发电机的电压、电流和磁链矢量，可由αβ轴分量表示为u=u_α+ju_β，i=i_α+ji_β，Ψ=Ψ_α+jΨ_β。上述模型采用发电机惯例，忽略了发电机磁路的非线性，且转子侧变量经过绕组折算到了定子侧。

由双馈风电系统的拓扑可知，发电机定子侧直接与电网相连，因此，式（6-5）中，定子电压u_s仅由电网决定；其转子电压u′_r由转子侧变流器决定，通过控制u′_r可调节发电机的输出。将式（6-5）中所有变量经过旋转变换到转子旋转坐标系下，转子电压u′_rr可由定子磁链和转子电流表示为[16]

式中，下角标“r”表示转子侧变量；上角标“r”表示在转子旋转坐标系下的变量；e′r_r0为定子磁链切割转子绕组而产生的感应反电动势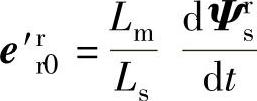，；σ=1-L²_m/（L_sL′_r）。

式（6-6）可由图6-15的等效电路表征。

由图6-15可知，双馈风电系统正常运行时，转子侧变流器的输出电压必须足够大，在抵消e′r_r0的前提下，还必须有足够的裕量控制转子电流以满足发电机转矩控制的要求。电网故障发生时，由于定子磁链不能突变，其将在转子绕组中感应出较大的瞬间反电动势e′r_r0，由后续分析可知，e′r_r0由可衰减和不可衰减两部分分量组成。由于转子侧变流器所能输出的最大电压幅值有限，当转子反电动势超过一定范围时，转子回路会产生较大的过电流，严重时甚至会导致变流器中的功率器件因过电流而损坏。为避免此类损坏，需要采取额外的保护措施，以保证变流器的安全运行。当反电动势e′r_r0中的可衰减分量以指数规律衰减为零后，若转子侧变流器容量足够，则转子侧变流器可恢复对发电机的控制能力，之后可通过转子侧变流器控制发电机转子电流的正负序分量，从而控制双馈发电系统满足并网导则的相关要求。

图6-15 转子旋转坐标系下双馈 发电机等效电路

6.3.1.1 电网故障对发电机定子磁链和转子侧反电动势的影响

假设故障前双馈发电机工作在正常状态，t=t₀时，发生电网故障，故障导致电网电压突降。故障前后电网电压的标幺值可以表示为

式中，p为故障后电网正序电压的跌落深度；q为故障后电网负序电压的含量；ω_g为电网频率；φ为故障前后电压矢量的相位角突变；上标+、-表示正负序分量。值得注意的是，式（6-7）中不含零序电压分量，因为发电机并网变压器为Yd联结，零序电压无法传递到发电机定子端。典型的电网故障特征已在本书第5章中作了详细介绍，上式中各变量可由第5章的相关分析得到，此处不再赘述。

忽略线路阻抗时，假设上述故障电压完全传递到发电机定子端，即u_s=u_g，ω_s=ω_g；进一步，忽略定子电阻，由式（6-5）可知，发电机定子磁链的稳态分量可由下式表示：

由式（6-5）、式（6-7）和式（6-8）可求解定子磁链的动态响应（其误差在10%～20%以内^[17]）为

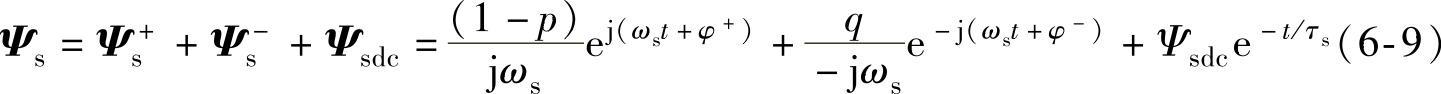
式中，τ_s为定子时间常数，τ_s=L_sσ/R_s；Ψ_sdc为故障后定子磁链直流分量的初始值，由于故障前后定子磁链无法突变，即Ψ_s（t₀-）=Ψ_s（t₀+），则Ψ_sdc可由式（6-9）求得为

由式（6-9）可知，t≥t₀时，定子磁链由可衰减和不可衰减两部分分量组成。其中，可衰减分量以指数规律衰减，它可保证定子电压变化后发电机磁链不产生突变。

由式（6-9），进一步考虑式（6-6）中e′_r0r的表达式，可求得转子侧感应电动势为

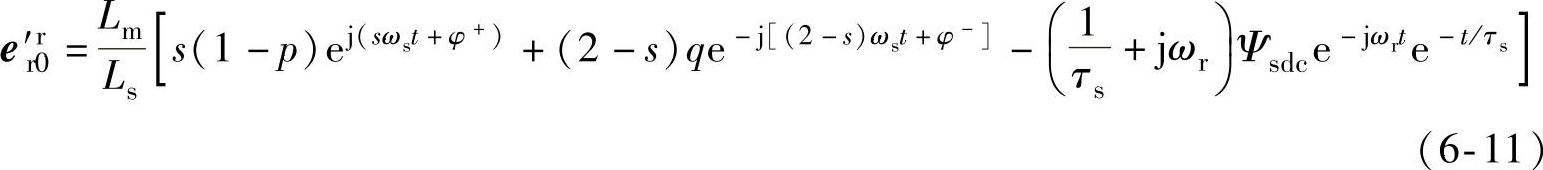
式中，s为双馈发电机的转差率，s=（ω_s-ω_r）/ω_s。

由式（6-11）可知，感应电动势e′_r0r包含三部分分量。第一部分分量与定子侧正序电压的跌落深度和发电机的转差率s（通常在±0.3以内）有关，该分量的频率较低，为转差角频率sω_s。第二部分分量与负序电压含量及（2-s）有关，其幅值较大，尤其是当双馈发电机工作在超同步区时，其幅值将超过负序电压幅值的两倍，该分量的角频率也较高，为（2-s）ω_s。上述两部分分量的相位分别与故障前后电网电压正负序分量的相位跳变有关。最后一部分分量取决于故障后定子磁链的初始值，该分量以指数规律逐渐减小，其角频率为转子角频率ω_r。值得注意的是，式（6-11）中所有转子侧分量都已折算到定子侧，考虑定转子绕组匝数比，转子绕组感应电动势相对于转子额定工作电压（额定转差频率工作时的转子电压）的标幺值可由以下反变换得到：(www.xing528.com)

式中，e^r_r0为转子绕组反电动势的真实值；s₀为双馈发电机额定转差率；K_sr为定转子绕组的匝数比，其典型值为1/3左右。增加匝数比K_sr或减小双馈发电机的转速运行范围，都可降低故障后转子绕组的反电动势，从而有利于双馈发电机的低电压穿越，然而上述措施会增加系统成本或降低系统运行效率，因此并不实际。

6.3.1.2 不同电网故障下双馈发电机的动态特性分析

由式（6-9）和式（6-11）可得不同故障条件下定子磁链矢量的变化轨迹和转子绕组反电动势的动态变化曲线，如图6-16所示。图中，电网故障发生在t=0时刻，故障前，定子磁链标幺值为Ψ_sα=0，Ψ_sβ=-1。典型的电网故障参数可由第5章的式（5-5）～式（5-7）计算得到（根据故障点位置和电网结构确定若干组λ、α值，代入式（5-5）～式（5-7）可计算得到正负序电压分量的幅值和相位），双馈发电机参数详见附录B表B-8。

如图6-16a所示，三相故障情况下，故障前后，双馈发电机定子磁链空间矢量的稳态运行轨迹均为同心圓；故障后，因电网电压幅值降低，轨迹圓的直径沿圓心方向减小。由图6-16b知，若故障后电网电压存在相位跳变，则转子反电动势的初始值较大，有可能超过1pu。当风电场通过地下交流电缆并网时，与传统架空传输线相比，故障后，电网电压的相位角跳变较大，使得双馈风电机组转子反电动势初始值较大，因而此结构下，双馈风电机组的低电压穿越较困难^[18]。然而值得注意的是，由于地下电缆的对地电容较大，电容效应将对电网电压起到一定的补偿作用，若故障距离相同，与传统架空传输线相比，采用地下电缆的结构，在发电机并网点处，其电压跌落深度较小。

不对称故障下，由于电网电压存在正负序分量，其空间矢量分别沿顺时针和逆时针方向旋转，因而定子磁链的稳态运行轨迹为椭圓。正负序电压矢量重合时，定子磁链矢量与椭圓轨迹的长轴重合；正负序电压矢量方向相反时，定子磁链矢量与椭圓轨迹的短轴重合，一个工频周期内，上述现象发生两次。

单相对地故障条件下，定子磁链变化轨迹和转子反电动势的动态响应曲线如图6-16c、d所示。若故障发生在风电场并网变压器的高压端，即令λ=0并代入式（5-5）可得，故障后p=0.3，q=0.3，φ+=0°，φ-=-180°，进一步由式（6-10）可知，故障后定子磁链中直流分量为零，则故障后定子磁链轨迹即为其稳态轨迹，不存在直流分量的动态衰减过程，如图6-16c所示。若故障点位于远离变压器高压侧的传输线路上，即式（5-5）中λ≠0，则故障后发电机定子电压正负序分

图6-16 不同故障条件下定子磁链和转子反电势的动态响应（s=-0.3）

图6-16 不同故障条件下定子磁链和转子反电势的动态响应（s=-0.3）（续）

量出现相位角跳变，定子磁链直流分量不为零，其典型变化轨迹如图6-16d所示。由于定子磁链中直流分量不为零，转子绕组感应电动势的初始值高于其稳态值，存在可衰减分量。由式（6-11）可推断，当电网电压跌落和相位角跳变同时出现且达到最大时，对应转子绕组感应电动势的初始值达到最大。当然，这种情况几乎不会出现，由本书5.2.2.2节的相关分析和图5-10可知，在实际电网中，故障点距离风电场越近，电压跌落越大，但此时相位角跳变却越小。

相间短路故障条件下，定子磁链变化轨迹和转子反电动势的动态响应如图6-16e、f所示。若故障发生在风电场并网变压器的高压端（即λ=0），则由图5-10可知，此故障下，定子电压中负序分量达到最大（0.5pu）；此时，定子电压正序分量也为0.5pu，因而故障后，定子磁链轨迹所形成的椭圓短轴长度为零（对应正负序电压矢量反相）；由于负序电压分量较高，即使不存在相位角跳变，故障后转子绕组反电动势初始值也较大，已达到2.1pu，其稳态值高于1pu。若故障点距离增加，相位角跳变会引起反电动势初始值的增加，但此时电压跌落深度也会减小，这将抵消相位角跳变所带来的影响。

两相对地短路故障的情况与相间短路故障相似，定子磁链变化轨迹和转子反电动势的动态响应如图6-16g、h所示。不过，此条件下，故障后负序电压分量的幅值低于相间短路故障的情况，转子反电动势的稳态值低于1pu，故障持续期间，发电机可保持可控性。

由图6-16比较可见，所有类型的故障中，相间短路所引起的转子绕组反电动势最大，因而是双馈风电机组低压穿越最难实现的一种情形。在图6-16e所示的极限条件下，故障后转子反电动势的稳态值已高于1pu，为保证故障持续阶段双馈发电机可控，从而满足并网导则的需要，必须重新设计转子变流器的控制算法；严重情况下，还必须对转子侧变流器进行扩容或升高变流器直流母线电压，亦或重新设计发电机参数（定转子匝数比或转差频率范围）。

综合图6-16的结果和上面的分析，可得到以下结论：

1）若转子侧变流器不作扩容处理，为实现所有故障条件下的低电压穿越，辅助穿越设备，如撬棒电路是必需的。图6-16所示的大部分故障条件下，故障后双馈发电机转子反电动势的初始值都已超过1pu，传统设计的转子侧变流器，其直流母线一般为转子侧额定电压的1.1～1.2倍，难以保证故障瞬间转子电流可控。当然，若故障不严重或电压跌路深度较浅，转子侧变流器可以保证转子电流受控，此时没有必要启用撬棒电路等辅助穿越设备。由低电压故障穿越并网导则的规定可知，故障后的第一阶段，需要尽快衰减掉定子磁链中的可衰减分量，使得转子变流器迅速回到可控区。从这个角度来看，不管故障是否严重，采用撬棒电路的方法似乎优于采用转子侧变流器的方法，因为撬棒电路接入时，定子磁链直流分量的衰减速度较快。

2）故障持续阶段，双馈风电机组必须根据并网导则的要求控制发电机输出一定的有功或无功电流，以支撑电网。为此，转子侧变流器应具有一定的可控裕度，即其输出电压在抵消掉转子反电动势的前提下，仍有足够裕量控制转子电流，从而使发电机输出给定的有功或无功电流。由图6-16可知，故障持续阶段，相间短路故障导致的发电机转子反电动势最高，严重故障下会超过1pu，为避免撬棒电路的重复投切，此时有必要考察转子变流器的控制能力；若无法满足控制要求，需要对转子侧变流器进行扩容或增加变流器直流母线电压，亦或重新设计发电机参数。值得注意的是，上述结论稍显保守，因其分析并未考虑发电机机端与GCP之间输电线路和变压器的阻抗，当考虑上述阻抗影响时，故障后发电机机端正序电压跌落和负序电压分量将低于理论分析值，上述结论还可适当放宽。

3）结论2）只考虑了发电机的最低控制要求，即故障持续过程中发电机保持不脱网运行。不对称故障下，若需要实现额外的控制目标，如消除发电机的转矩脉动，则还需要进一步考虑发电机负序电流的控制要求。值得注意的是，转子侧变流器对发电机正负序电流的控制能力完全不同。由图6-15可知，稳态条件下，发电机转子电流正负序分量分别为

式中，分别为控制转子正、负序电流所需的正、负序电压分量。由于图6-15所示电路建立在转子旋转坐标系下，则定子坐标系下的正、负序分量在图6-15所示电路中的角频率分别为。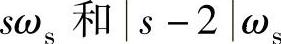

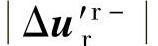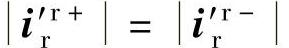忽略较小的转子电阻，由式（6-13）可知，若需要发电机输出相等幅值的正负序转子电流，则所需负序电压分量幅值为正序电压分量幅值的倍。若s=-0.2，可计算知，若要，需要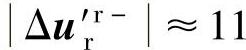Δu′r+r，这意味着转子侧变流器对负序电流分量的控制能力远小于正序电流分量。由于变流器直流母线电压受限，严重不对称故障下，控制发电机正序电流分量，剩余容量用于控制负序电流分量；若不对称故障较轻，则可同时控制发电机的正负序电流分量，在满足并网导则的基础上优化发电机的输出性能^[18]。

4）故障恢复阶段，因发电机输出有功和无功功率可独立受控，并网导则规定的功率恢复要求较容易得到满足。然而，由于此阶段仍可能存在相位角跳变，故障恢复时，转子反电动势会因此出现较大的瞬间值，因而此阶段撬棒电路等辅助设备可能会再次启用。此外，若故障恢复速度较快，考虑到风电机组无功补偿装置或风电场并网变压器变分接头动作的滞后，此阶段风电场并网点可能会出现局部过电压，为保证风电机组的不脱网运行，此阶段的高电压穿越也需进一步考虑。事实上，局部过电压目前已成为我国已建成大型风电场脱网事故的主要诱因之一。