静止坐标系下的锁相环性能优化

将基于静止坐标系下的PD和二阶自适应滤波器结合，也可实现三相电压信号的正负序分离。静止坐标系下锁相环的基本结构如图5-28所示，两相静止坐标下的电压分量u_α、u_β分别经二阶自适应滤波器（SOAF）后得到基波电压u′_α、u′_β及相位移90°后的电压信号qu′_α、qu′_β，由式（5-21）可知，通过简单的数学计算，即可分离出正负序电压分量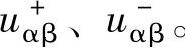

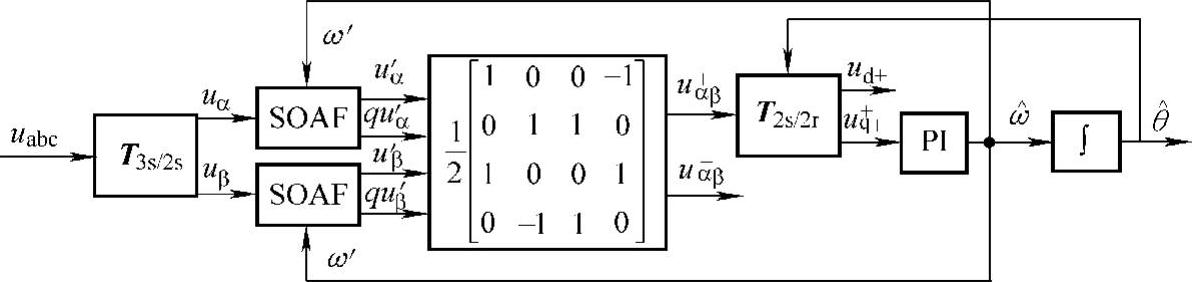
图5-28 基于静止坐标系锁相环的基本结构

图5-28中，二阶自适应滤波器的实现形式有多种，其中以二阶广义积分器（见图5-15）为核心的自适应滤波器实现简单、性能优越，比较适合于实际工程应用。需要注意的是，图5-28中二阶自适应滤波器的参考输入ω′可由锁相环的正序电压分量经锁频后得到，图中的锁频环节与图5-18中所采用的一致，其原理此处不再赘述。当然，图中的锁频环节也可采用其他结构^[22]，其功能都是为了增强锁相环对电网电压频率波动的鲁棒性。以检测正序电压分量为例，上述方法的仿真结果如图5-29所示。仿真中，电网故障发生在t=0.1～0.2s，故障后电网电压从u+=1∠0°pu变化为

u+=0.75∠0°pu，u-=0.15∠0°pu。(www.xing528.com)

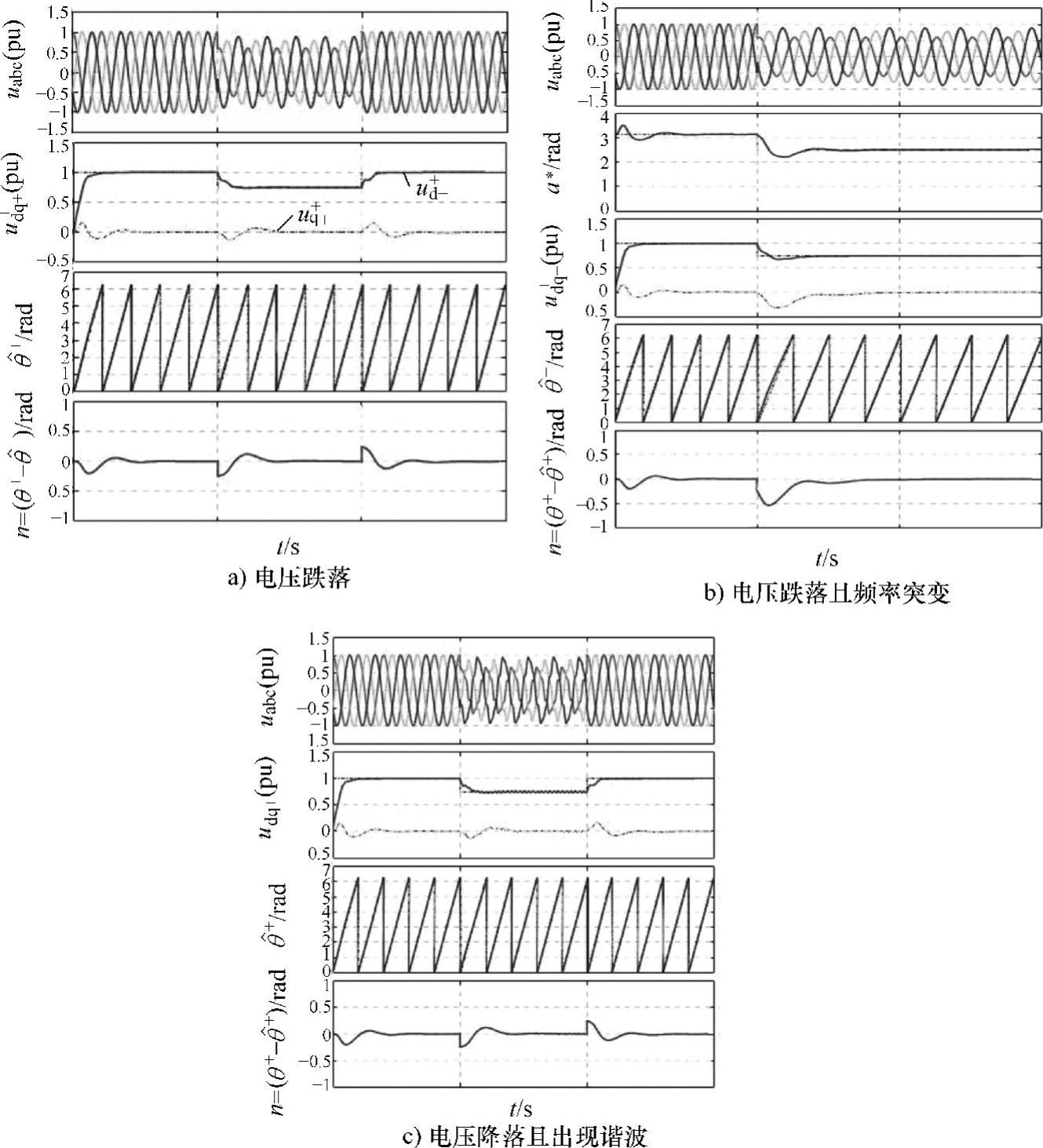
图5-29 基于SOGI锁相环的仿真结果

图5-29a～c分别为仅出现电网电压跌落、电网电压跌落伴随频率突变（从50Hz突降为40Hz）和电网电压跌落伴随电网谐波电压（u^-5=0.07∠-60°pu且u⁺⁷=0.05∠30°pu）的三种情况。结果表明，在上述各种故障条件下，该方法都可实现正负序电压分量的快速检测。

除了上述介绍的锁相环外，在静止坐标系下还可采用其他方法实现锁相，但与上面介绍的锁相环相比，其他方法所采用的PD环节与之相同，LF环节有所区别。例如，参考文献^[18]所提出基于静止坐标系的锁相环在LF环节中采用了复杂的正交信号发生器和鉴频环节以代替前述的SOGI滤波器；参考文献^[19]所设计锁相环的LF环节在SOGI滤波器基础上作了一定的改进。以上方法的基本原理和效果与基于SOGI的锁相环相似，其实现更为复杂，此处不再一一介绍。