旋转坐标系锁相环优化设计方案

在正序（负序）同步旋转坐标系中，两相正序（负序）信号为直流分量，两相负序信号为两倍频的交流分量，滤除相应的交流分量后，得分离出正序（负序）信号。

5.2.2.1 基本原理

以获取正序电压分量为例，基于旋转坐标系锁相环的基本结构如图5-18所示。图中，LPF为低通滤波器，PI为比例积分环节。若三相电压变量如式（5-15）所示，则根据式（5-11）和式（5-13）将其变换到正序旋转坐标系下，可得

式中，θ^+为图5-18所示锁相环输出的正序电压矢量的相位角信号，若锁相成功，达到稳态时有θ^+=ωt，代入上式后可得到式（5-22）。

图5-18 基于旋转坐标系锁相环的基本结构

图5-18所示的锁相环节为非线性结构，可基于其小信号线性模型分析其特性。在稳态工作点附近（即），式（5-28）中的各项近似有

代入式（5-28），可得到图5-18所示锁相环节的小信号线性模型，如图5-19所示^[25]。

图5-19 图5-18所示锁相环的小信号线性模型

图中，Θ（s），Θ′（s），Θ^（s）分别为θ+，θ+′，θ^+的拉普拉斯变换，θ+′（t）为负序电压分量引起的附加相移，可视为锁相环的扰动输入，θ+′（t）=-U-_sin（2ωt+ϕ-）。

图5.2-9所示的小信号线性模型的输出-输入和输出-扰动关系可由以下传递函数表示：

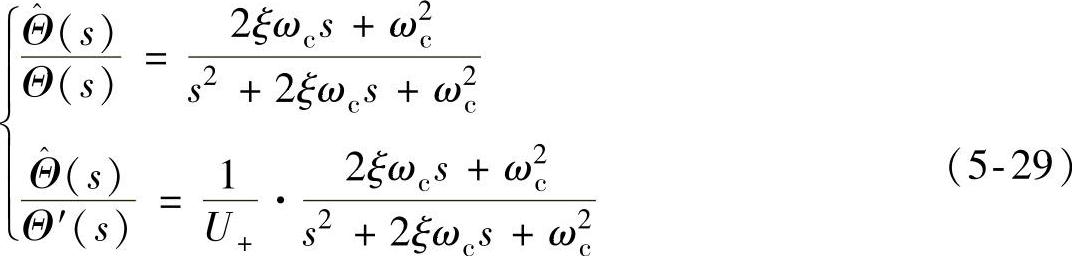
式中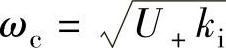，，。易知，上式所表示系统的所有特征根都在左半平面，系统稳定。进一步，输出-输入和输出-扰动呈典型的二阶低通滤波特性，一方面，输入信号θ+中的噪声及谐波信号可被滤除，不会传递到输出；另一方面，通过合理设计式（5-29）中的截止角频率ω_c，使其低于扰动信号θ+′的角频率2ω，则负序分量引起的附加相移θ+′也可被滤除。ω_c越低，滤波效果越好，θ+′对输出θ^_+的影响越小。

采用与图5-18所示的同样方法，在负序旋转坐标系下，也可实现负序分量的检测。

然而，上述方法存在动态响应速度与检测准确度的矛盾。为满足一定的检测准确度，需要设计较低的截止角频率ω_c，但锁相环的动态响应速度将因此变慢，在某些对锁相速度要求较高的场合，如电网频率变化剧烈的场合，该锁相环并不实用。相关分析详见参考文献^[26]。

为了在不影响检测准确度的前提下提高检测速度，可以采用基于双旋转坐标系且具有前馈解耦环节的锁相环^[14]。

5.2.2.2 解耦双旋转坐标系锁相环（DDSRF-PLL）

在图5-18的基础上增加交叉解耦项，可得到解耦双旋转坐标系锁相环，其基本结构如图5-20所示^[14]。图中，交叉解耦环节的控制框图如图5-21所示。以正序电压分量的检测为例，当闭环系统达到稳态时，若’，则交叉耦合项分别为

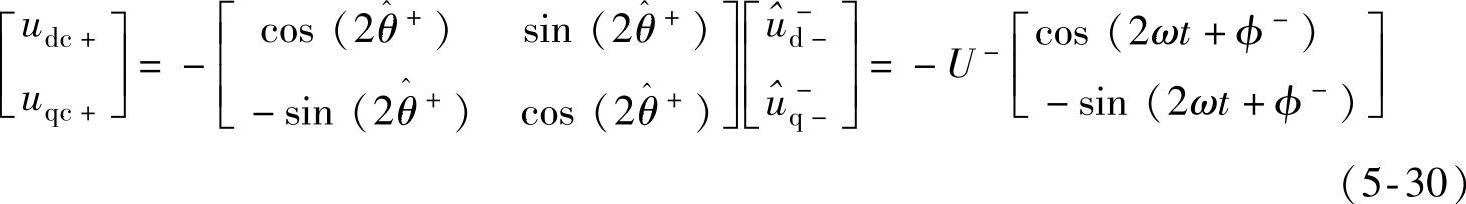
式中，u_dc+，u_qc+为前馈解耦项；稳态时，负序旋转坐标下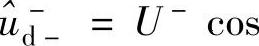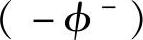，，。由式（5-22）可知，稳态时，前馈解耦分量可以完全抵消正序旋转变换后电压分量中的两倍频负序脉动分量，实现正序分量的检测；同理，负序旋转坐标下也可通过类似前馈解耦实现负序分量的检测。动态过程中，上述前馈解耦项可提高锁相速度，适用于如低电压穿越控制等对电压检测速度和准确度要求均较高的场合。

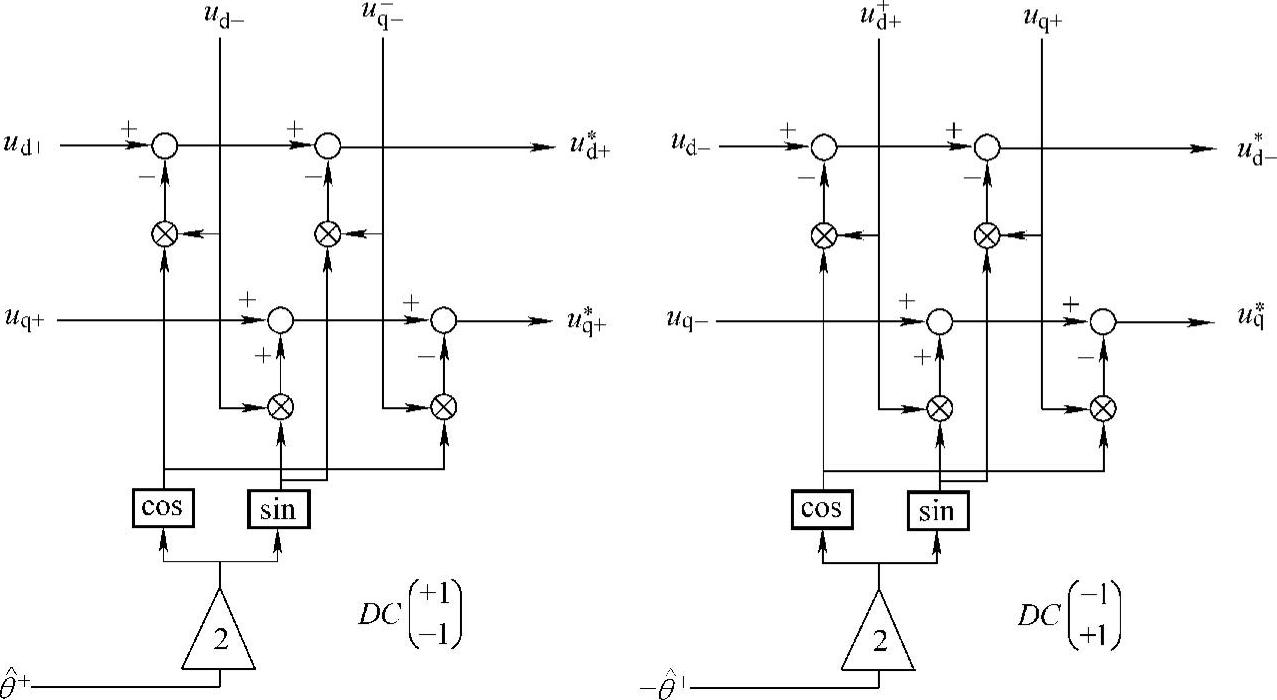
图5-20 解耦双旋转坐标系锁相环的控制框图

(www.xing528.com)

图5-21 图5-20中交叉解耦环节的控制框图

通过仿真对上述方法的有效性进行验证，以检测正序电压分量为例，其结果如图5-22所示^[14]。仿真中，电网故障发生在t=0时刻，故障后的系统参数为

u+=1.0∠0°pu，u-=0.3∠0°pu，kp=2.22，k i=246.7

若电压信号中不含谐波分量，由图5-22a可知，该方法可在一个工频周期内实现正负序电压的快速检测；若电压信号中含谐波分量（正序和负序5次谐波同时存在，且U⁺⁵=0.1∠0°pu，U^-5=0.1∠0°pu），由图5-22b可知，检测结果中出现了谐波分量，但由于闭环系统中低通滤波环节的作用，该谐波含量较小，检测准确度仍然较高。

图5-22 解耦双旋转坐标系锁相环的仿真结果

5.2.2.3 基于延时滤波器的锁相环（DSCF-PLL）

若电网电压不含谐波信号，式（5-22）、式（5-23）中的两倍频分量也可用延时滤波器滤除，该滤波器并不影响直流分量的动态响应，因而基于延时滤波器的锁相环响应速度也较快。设电网工频周期T=2π/ω，可设计延时滤波器DSC[u]为

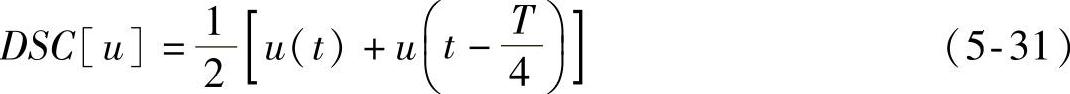
式（5-22）、式（5-23）所得正负序旋转坐标下的电压分量经滤波后得到

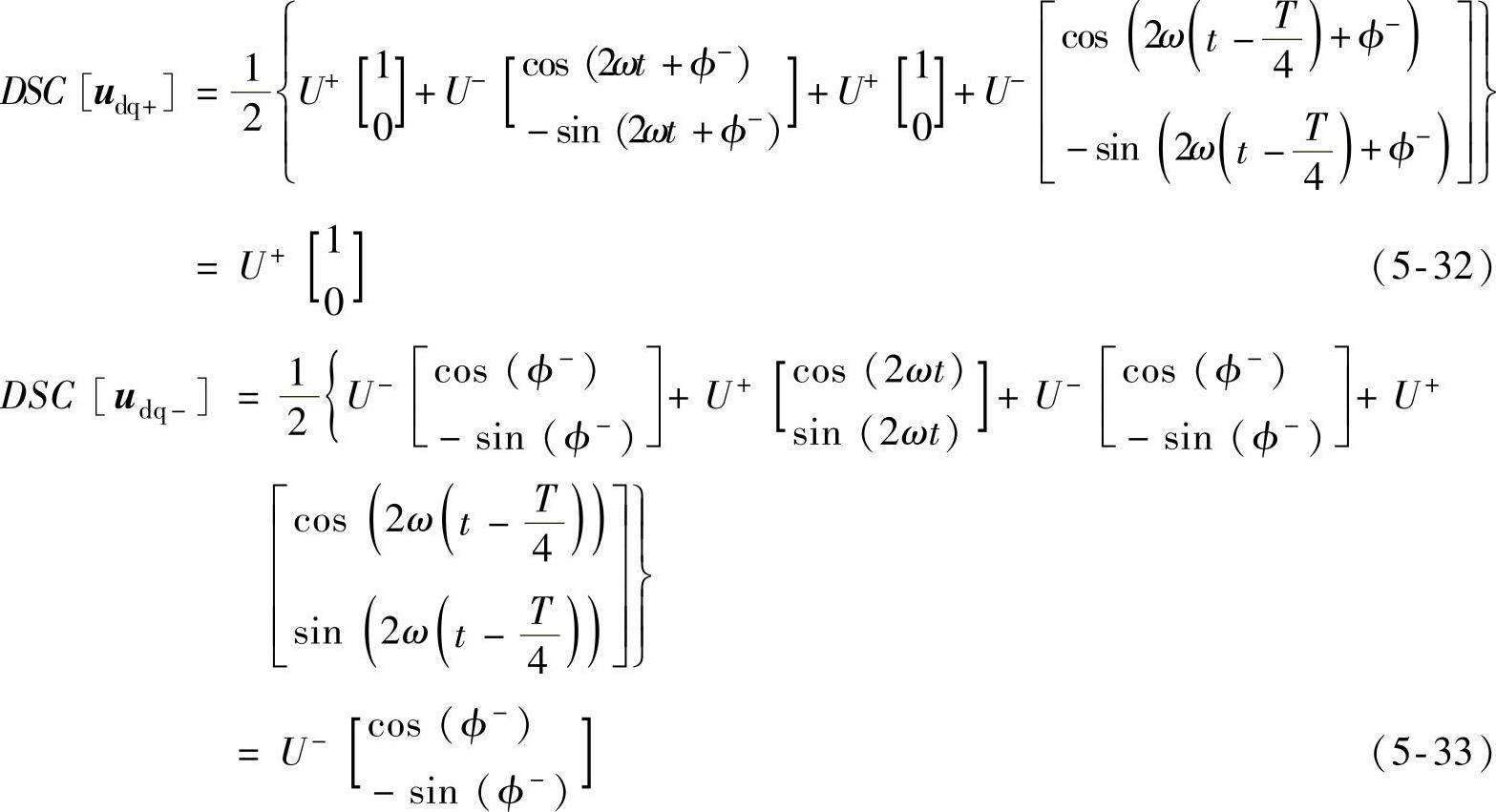
以u_d+为例，上述滤波过程可由图5-23表示，可见延时后的电压信号与延时前信号大小相等、方向相反，可完全抵消。

图5-23 DSC工作原理示意图

利用延时滤波器构成锁相环，其结构如图5-24所示。该方法的最大检测延时为1/4工频周期，检测速度较快，然而电网电压信号中的谐波分量会影响其检测性能。不同于传统低通滤波器，延时滤波器只能滤除特定次的谐波信号，由式（5-31）可知，+5、-7、+11、-13等次谐波经延时滤波器后可被消除，而-5、+7、-11、+13等次谐波经延时滤波后反而会被放大。为解决此问题，可以使用基于级联延时滤波器的锁相环（Cascaded Delayed Signal Cancellation Filter-PLL，CDSCF-PLL）^[27]，其结构如图5-25所示，其中，DSCF_n表示T/n周期延时滤波器，采用级联模块的效果是明显的，例如只用DSCF₄时，可消除静止坐标系下负序基波和部分奇次谐波，而使用DSCF₂、DSCF₄、DSCF₈、DSCF₁₆四个模块级联即可消除包括直流偏置在内的不高于30次的所有谐波^[27]。值得注意的是，多级延时滤波器一方面会导致实现锁相环所需的计算量和数据存储量增大；另一方面增加了锁相的延时，降低了锁相速度。

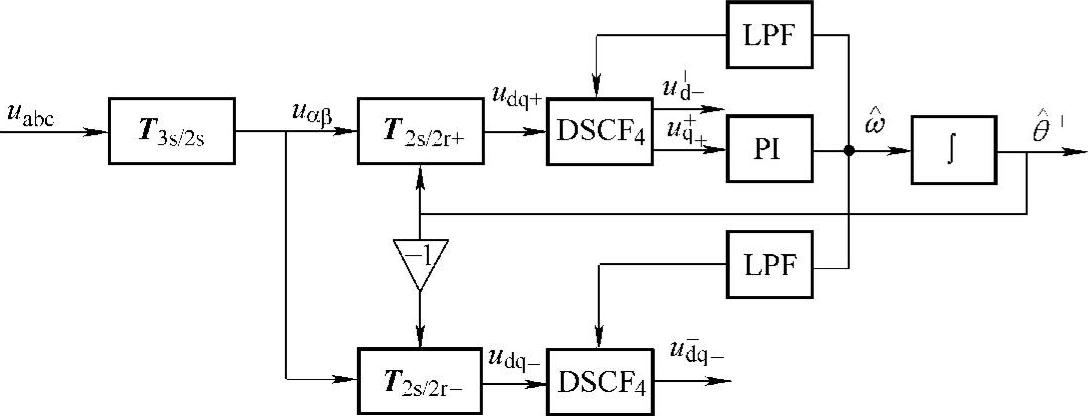
图5-24 基于延时滤波器的锁相环控制框图

图5-25 基于级联延时滤波器的锁相环控制框图

以检测正序电压分量为例，上述方法的仿真结果如图5-26和图5-27所示。仿真中，电网故障发生在t=0.05s时刻，故障后的系统参数为u+=0.7∠-30°pu，u-=0.3∠0°pu，图a、b分别为基于三级延时滤波器和四级延时滤波器锁相环的仿真结果。若电压信号中不含谐波分量，由图5-26可知，基于两种延时滤波器的锁相环均可在一个工频周期内实现正负序电压的快速检测；若电压信号中含谐波分量，由图5-27可知，对于特定次谐波，需采用特定的DSC进行滤除，当被测信号中谐波频谱和含量较丰富时（图5-27a中，被测信号所含奇数次谐波的次数为h=-5，+7，-11，+13，-17，+19，相量大小为U^h=1.0/（2h）∠0°pu，偶数次谐波的次数为h=-2，+4，-8，+10，-14，+16，-20，相量大小为U^h=1.0/（8h）∠0°pu，总谐波含量为16%；图5-27b中，谐波次数为h=±5，±7，±11，±13，幅值为U^h=1.0/（2h）∠0°pu，总谐波含量为27.3%），基于多级DSCF的锁相环可实现较准确的正负序信号分离。

除以上方法外，旋转坐标系下的锁相环还有其他实现手段^[28，29]，然而其核心思想和工作原理与上面介绍的方法并无较大差异，在此不再赘述。

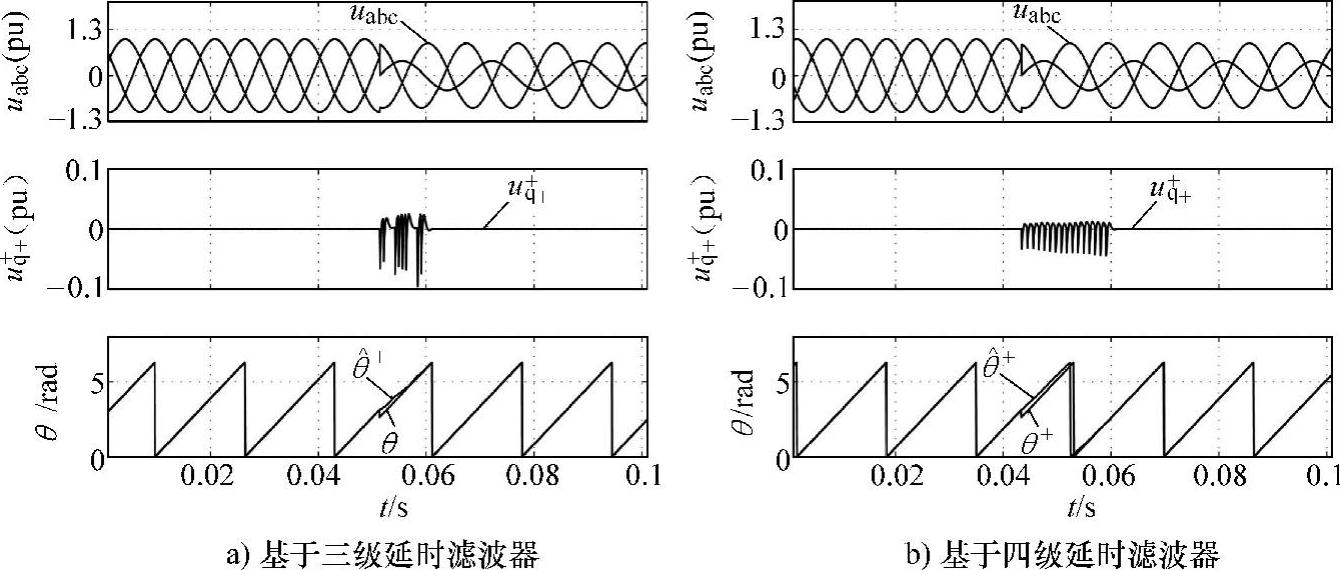
图5-26 基于延时滤波器锁相环的仿真结果（电压信号不含电压谐波）

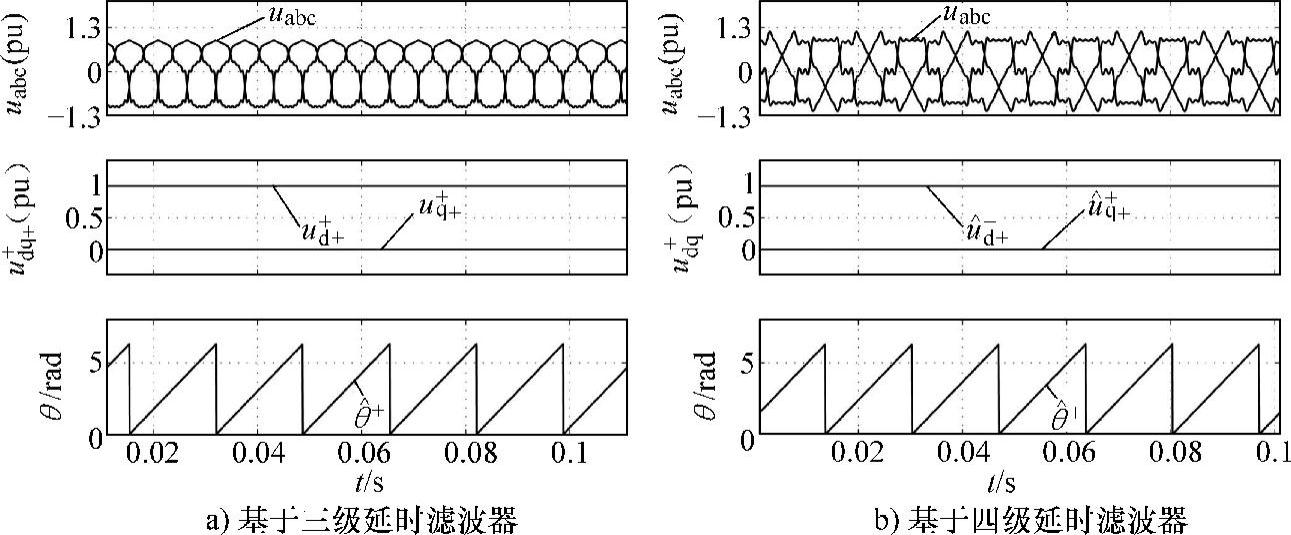
图5-27 基于延时滤波器锁相环的仿真结果（电压信号含电压谐波）