锁相环的一般结构及应用探讨

锁相环的实现方法很多，可由硬件实现，也可由软件实现^[11]；可采用开环结构，也可采用闭环结构；可基于频域实现，也可基于时域实现。开环锁相环实现简单、成本低，但抗扰性较差，在电网电压有谐波等条件下，其性能较差；与之相比，闭环锁相环对电压扰动的鲁棒性强、检测准确度高，应用更为广泛。对于闭环锁相环，无论采用何种方法实现，其基本结构相似，包括三个组成部分：鉴相器（Phase Detector，PD）、环路滤波器（Loop Filter，LF）和压控振荡器（Voltage Controlled Oscillator，VCO），其结构如图5-11所示^[12]。

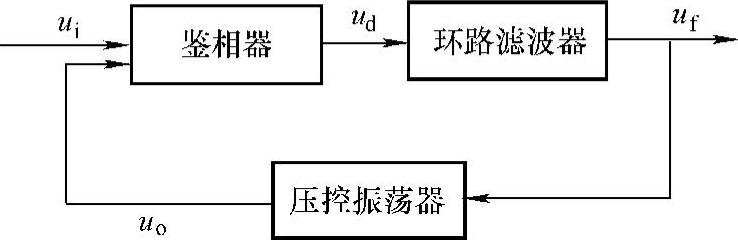
图5-11 锁相环的基本结构

PD模块的输入为被测电压信号和VCO的输出信号，PD检测两者的差值，并通过放大器将该误差信号放大后输出信号u_d，u_d经LF滤波后输出检测结果u_f，u_f作为VCO的输入，不断调整其振荡输出，形成闭环系统。当系统进入稳态时，输出u_f完全跟踪输入，锁相过程结束。

5.2.1.1 硬件锁相环

早期的锁相环都是基于硬件实现的，图5-11所示的三个部分由分立元件和模拟电路构成；随着集成电路的快速发展，硬件锁相环现已实现全数字化和集成化，如德州仪器（Texas Instruments，TI）公司生产的74LS297芯片^[13]，其PD、VCO和LF都采用全数字电路实现，可实现电网电压的快速检测，目前已被广泛应用于电力系统的监测和保护之中。随着可编程数字芯片技术的发展，通过改进图5-11所示三部分的硬件电路，可实现更高性能的锁相环，如参考文献^[11]所述的即是基于现场可编程门阵列（FPGA）实现了一种锁相速度更快、范围更广、准确度更高的全数字锁相环。硬件锁相环的优点是成本较低、性能可靠、结构和运算都比较简单，非常适用于低成本、可靠性要求高的应用场合；其缺点在于仅适用于单相系统的锁相，无法用于检测三相系统的正负序电压分量。当然，上述观点并非绝对，结合电压瞬时值检测和简单的计算模块，硬件锁相环也可扩展到三相系统的正负序电压检测中^[11]，然而这是以增加复杂度和成本为代价的。硬件锁相环不作为本书的重点，有兴趣的读者可进一步参阅参考文献^[11]。

5.2.1.2 软件锁相环

软件锁相环在三相系统中使用较广泛，其实现前提是实时检测三相电压信号，且需要大量复杂的数值计算。在新能源并网发电系统的应用中，为控制变流器以实现系统的功率调节和保护，通常需要实时检测电网电压和系统输出电流，且会配备具有强大计算能力的微处理器，如数字信号处理器（Digital Signal Processor，DSP）。基于已有的硬件条件，软件锁相环可被容易地嵌入到系统的控制软件中，因而在该领域得到了广泛应用。

软件锁相环的基本结构也可由图5-11表示，然而与硬件锁相环不同，软件锁相环中的PD和VCO通常合二为一，很难将它们区分开来，用不同方法实现的软件锁相环主要在PD和LF两个部分有所区别。

对于三相软件锁相环，其PD可基于旋转或静止坐标系构建；根据频率响应的不同，其LF有低通、陷波、延时、二阶自适应滤波器等多种形式。根据PD和LF的不同组合，可以得到不同结构和特性的软件锁相环，见表5-1。

表5-1 不同结构的三相软件锁相环

（续）

注：LPF（Low Pass Filter）：低通滤波器；DSCF（Delayed Signal Cancellation Filter）：延时滤波器；SOAF（Second Order Adaptive Filter）：二阶自适应滤波器；DDSRF（Decoupled Double Synchronous Reference Frame）：解耦双旋转坐标系；IPTF（Inverse Park Transformation Frame）：反Park变换坐标系；DSOAF（Double Second Order Adaptive Filter）：双二阶自适应滤波器；FRF（Fixed Reference Frame）：静止坐标系；SSI（Sinusoidal Signal Integrators）：正弦积分器。

1.参考坐标系变换

对于三相系统，参考坐标系理论不仅可简化系统分析，还有利于相关控制策略的计算机仿真和数字化实现。在众多参考坐标系中，三相静止坐标系（即abc坐标系）、两相静止坐标系（αβ坐标系）和旋转坐标系（dq坐标系）得到了最为广泛的应用^[20]。

对于三相对称系统，以电压变量为例，在abc静止坐标系下，三相电压变量可表示为

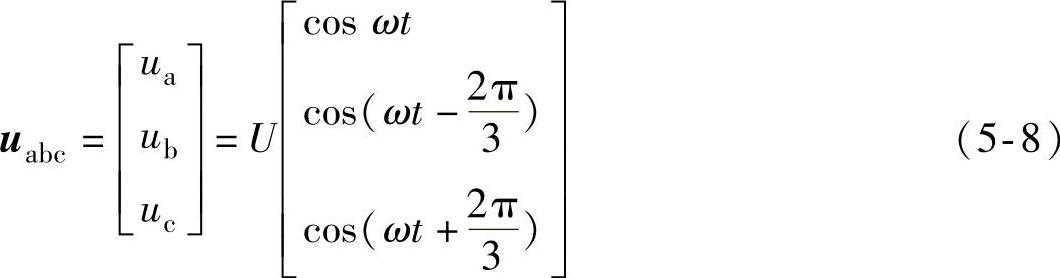
式中，U为三相电压幅值；ω为电压角频率；假设a相电压初始相位角为0。

选择平面内三个互差120°的单位矢量

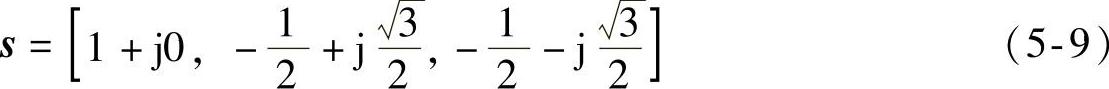
对式（5-8）、式（5-9）求内积，可得电压空间矢量u，该电压矢量可用以表征三相电压的幅值、角频率和初始相位角，其与对应的三相电压之间的关系如图5-12所示，相对于abc静止坐标系而言，u沿逆时针方向以电压角频率ω同步旋转。

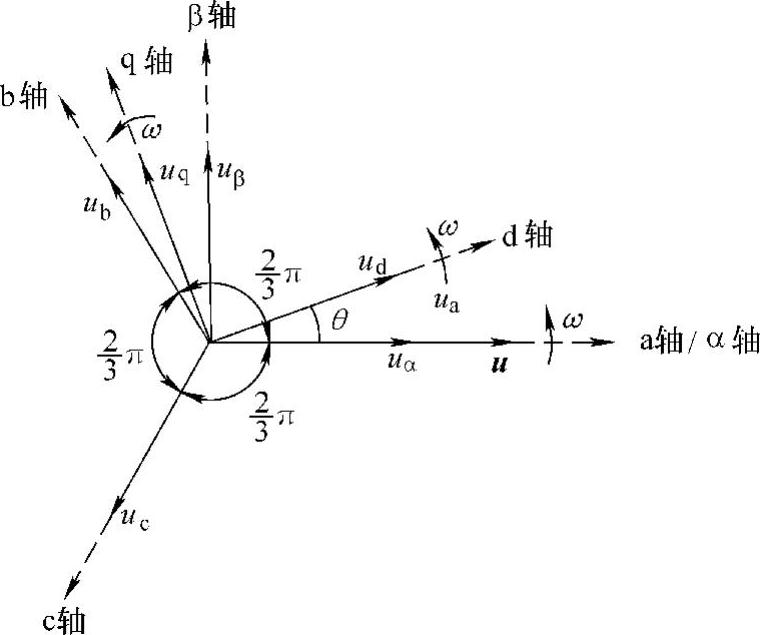
图5-12 不同坐标系下三相电压分量的关系

对于三相三线制系统，由于式（5-8）所示三相电压变量线性相关，即有u_a+u_b+u_c=0，abc静止坐标系中的三相变量还可用两相静止αβ坐标系中的线性无关（相互解耦）的两个变量表示为

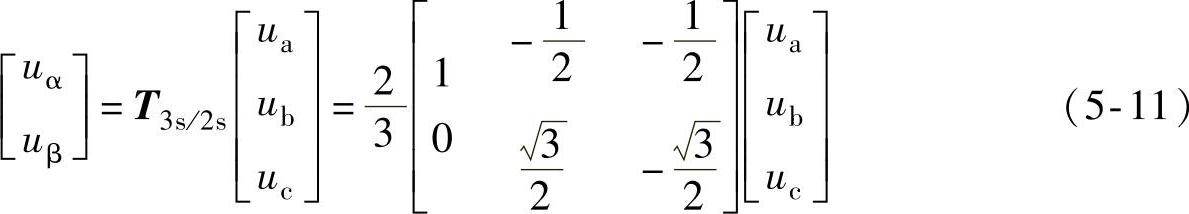
两相和三相静止坐标系之间的关系及式（5-11）所示的u_α、u_β和u_a、u_b、u_c的关系也如图5-12所示，其中，α轴与a轴重合，β轴超前α轴90°。相应地，静止坐标系下的两相到三相变量之间的变换可通过下式实现：

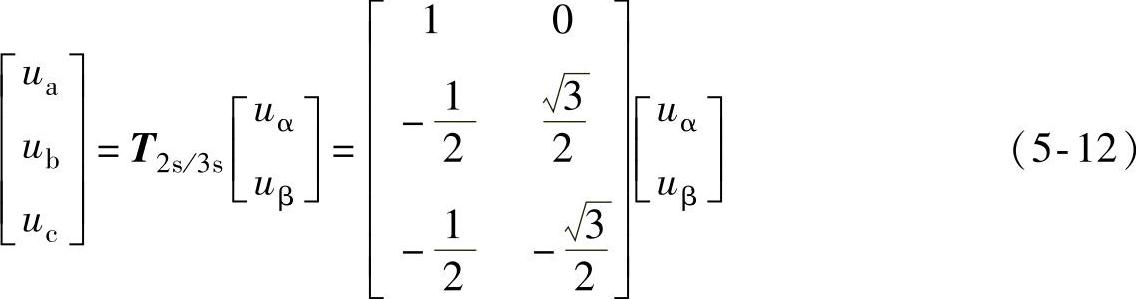
静止坐标系下的变量还可以通过以下帕克变换（Park Transformation）或称为旋转变换变换为旋转坐标系（dq坐标系）下的两相变量。

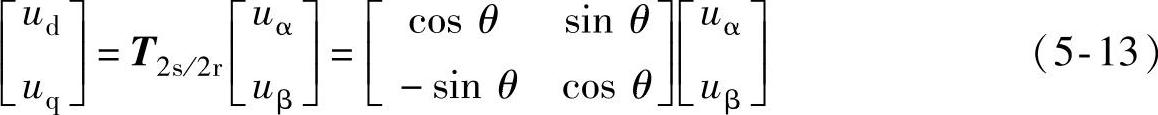
相应地，也可以通过如下逆变换将旋转坐标系中的dq轴变量变换为静止坐标系中的αβ轴变量。

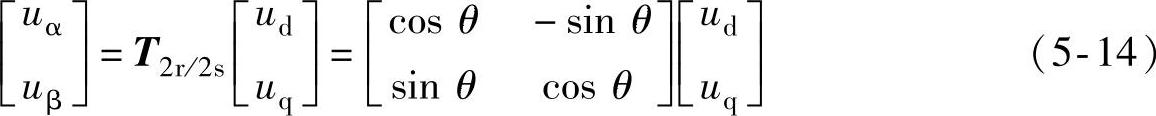
如图5-12所示，相对于abc和αβ静止坐标系而言，dq轴在空间以角速度ω旋转，若a轴和d轴之间的夹角为θ，则有ω=dθ/dt。此坐标系下，三相电压变量可由两相独立的直流变量表示。该坐标系常被用于三相发电系统的控制和分析。

在电网发生不对称故障时，考虑Yd联结变压器对故障侧零序电压的隔离作用，若不考虑谐波分量，电网电压变量中只会出现负序分量，此时三相电压变量可以表示为

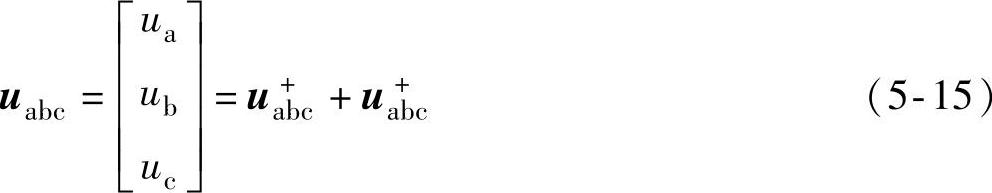
式中

式中，a相正序电压分量的初始相位角设为参考值零，其负序电压分量的初始相位角为ϕ-。ua+bc，ua-bc可由对称分量法或式（5-2）求得。

在两相静止αβ坐标系下，正负序电压分量可以表示为

式中，uα+β=[uα+，uβ+]T；uα-β=[uα-，uβ-]T。

将式（5-2）代入，则αβ坐标系下的序电压分量可由三相电压分量u_abc表示为

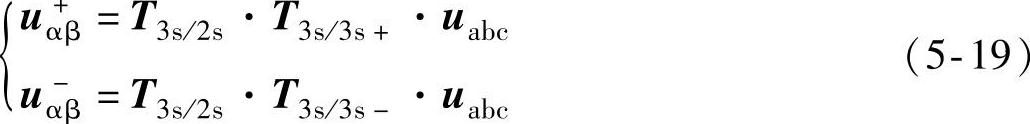
进一步，αβ坐标系下的序电压分量还可由两相电压分量u_αβ表示为(www.xing528.com)

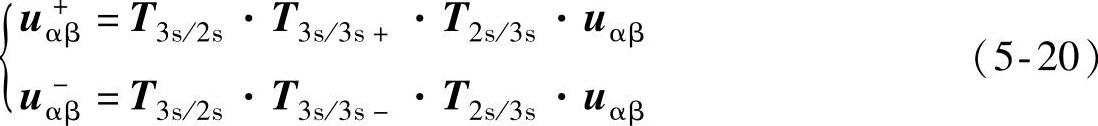
式（5-20）经化简后得到

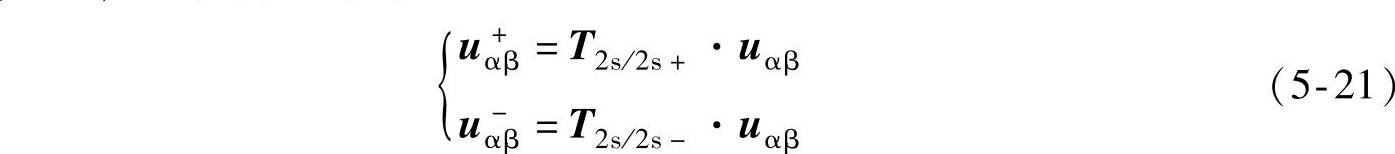
式中

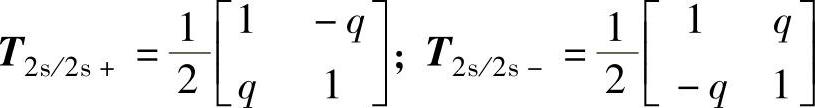
其中，q是90°相移算子，。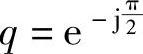

可见，在两相静止坐标系下，正负序电压分量可由两相电压变量u_αβ经过一定的相移和运算而得到。通过设计相移滤波器，即可由式（5-21）分离出正负序电压分量，这是基于静止坐标系实现锁相环的基本思路。

式（5-15）所表示的三相电压变量经式（5-11）和式（5-13）正序帕克变换可得到

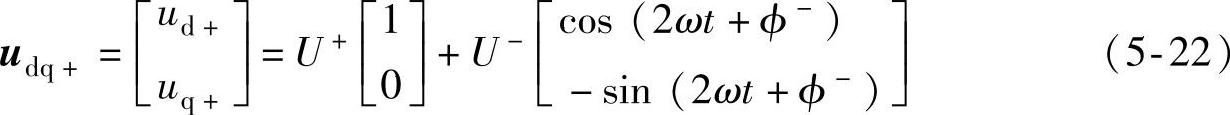
式中，下角标+、-分别表示正负序旋转坐标系下的变量。

可见，在正序同步旋转坐标系下，正序电压分量可由两相直流电压分量表示，而负序电压分量则变换为两相两倍旋转频率波动的交流分量。同理，在负序同步旋转坐标系下，负序电压分量可表示为两相直流电压分量，而正序电压分量则为两相两倍频的交流分量。

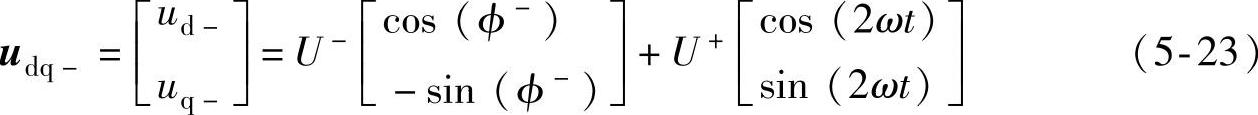
通过设计合适的滤波器滤除其中的交流分量，即可得到相应的序电压分量，这是基于旋转坐标系实现锁相环的基本思路。

由上述分析可知，不同坐标系下的鉴相环节必须配置不同特性的滤波器，才可实现正负序电压的检测，滤波器性能的优劣直接决定锁相的速度和准确度，因而是软件锁相环的核心环节，下面将介绍几种软件锁相环中常用的滤波器。

2.低通滤波器（LPF）

低通滤波器可以滤除信号中的高频分量，其最简单的形式为一阶低通滤波器，传递函数为

式中，G₀是零频增益；ω_c是截止角频率。

令G₀=1，ω_c=1rad/s，则一阶低通滤波器的典型幅频特性如图5-13所示。由佩利-维纳准则可知，理想的低通滤波器是不可实现的，图5-13所示低通滤波器中，当信号频率高于其截止频率时，信号幅值以-20dB/十倍频程（dec）的速率衰减。在基于旋转坐标系的锁相环中，为实现正负序电压分量的分离，往往采用低通滤波器滤除信号中的两倍频交流分量。若滤波器采用式（5-24）所示的一阶结构，则需设计其截止频率低于两倍频的交流频率（对应基波频率为50Hz的系统，截止频率需低于100Hz）。

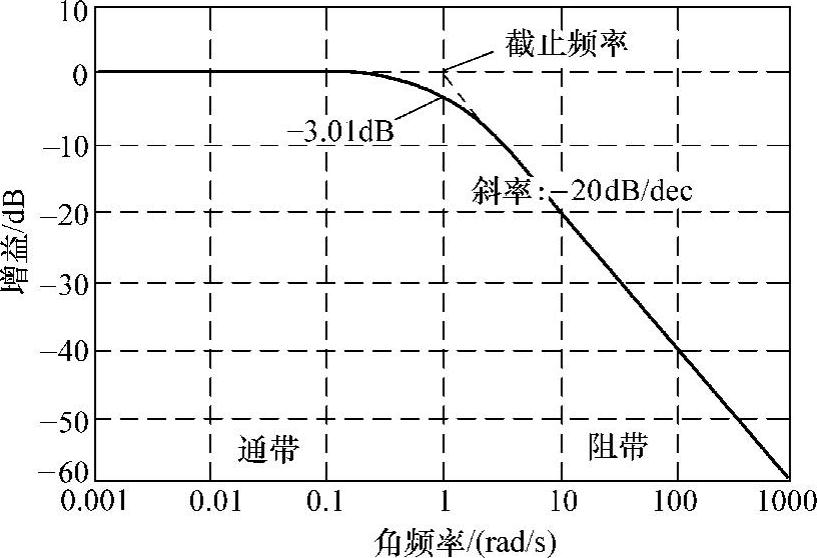
图5-13 一阶低通滤波器幅频特性

值得注意的是，除了滤除两倍频的交流分量外，低通滤波器还可同时滤除信号中的其他高频分量，因此若电压信号中含有谐波，基于旋转坐标系的锁相环也可顺利检测出基波电压的正负序分量。当然，锁相环的检测效果取决于低通滤波器对高频信号的滤波能力，选择更低的截止频率，有助于改善谐波信号对锁相准确度的影响，然而，此时锁相速度会受到影响^[21]。为降低低通滤波器的高频增益且不影响其低频增益，还可以采用高阶的低通滤波器，如二阶的巴特沃斯或切比雪夫滤波器^[21]等，在此不再赘述。

3.延时滤波器（DSC）

延时滤波器适用于噪声信号频率已知的场合，其原理比较简单直观：将噪声正弦信号延时半个周期，所得新信号与原信号大小相同、方向相反，将这两个信号叠加，结果为零，就可消除噪声，即

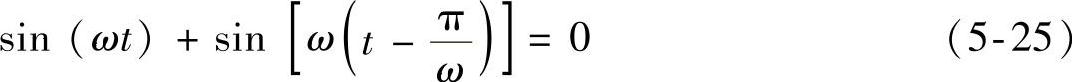
若已知噪声信号的频率，可利用式（5-25）的延迟滤波器消除此特定频率的噪声，该方法的数字化实现较容易^[16]。

基于旋转坐标系实现锁相环时，正序旋转坐标系中，正序电压信号为直流量，负序电压信号为两倍频交流分量，采用式（5-25）所示延迟信号滤波器，将延时1/4工频周期的信号与原信号叠加，可消除原信号中的两倍频交流（负序）分量，与此同时，直流（正序）分量的幅值被扩大两倍，可通过比例计算将其还原。

4.二阶自适应滤波器（SOAF）

二阶自适应滤波器本质上是一种针对正弦信号的带通滤波器，其基本结构如图5-14所示^[22]。若正弦输入信号u中含有噪声信号，另一路参考输入x经自适应滤波后得到不含噪声的正弦信号u′，u和u′的误差e被反馈回自适应滤波环节以调整u′。

实现图5-14中自适应滤波环节的方法很多，其中，二阶广义积分器（Second Or-der Generalized Integrator，SOGI）结构简单、计算复杂度低，更易被应用于实际系统。二阶广义积分器的设计思路来源于传统的广义积分器（Generalized Integrator，GI）^[22]，为双输入双输出闭环系统，由其构成二阶自适应滤波器的结构如图5-15所示。输入u、ω分别为正弦信号的瞬时值和角频率，输出为两路正交的正弦信号u′、u″，u″由u′经积分后得到。

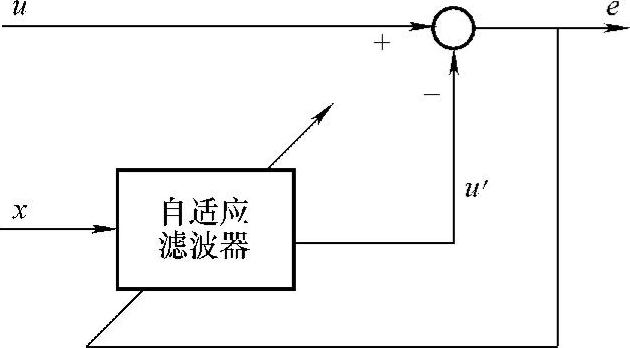
图5-14 二阶自适应滤波器基本结构

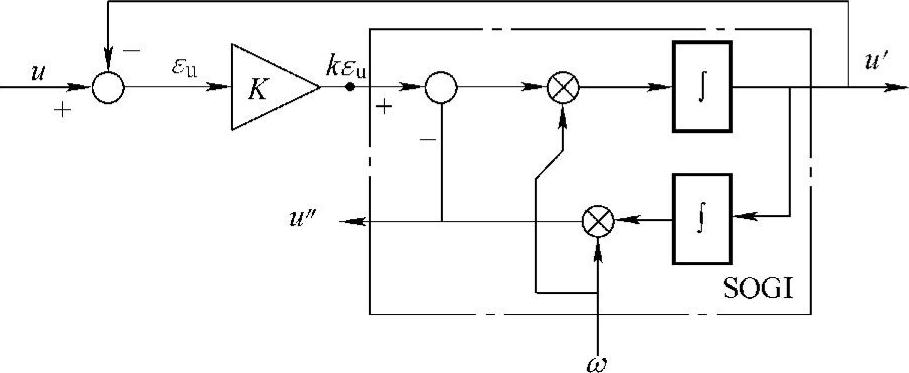
图5-15 基于SOGI的二阶自适应滤波器控制框图

图5-15中，滤波器的核心环节为SOGI，其传递函数为

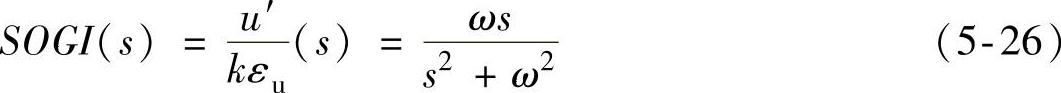
SOGI本质上是一种带通滤波器，当其中心频率ω取为电网角频率100π rad/s时，式（5-26）对应的幅频和相频特性如图5-16所示。对于中心频率处的信号，SOGI的增益非常大，相移为零；该带通滤波器的带宽非常窄，当信号频率稍稍偏移中心频率时，增益迅速衰减，因而该滤波器对于输入信号频率波动的鲁棒性较差。

进一步，由图5-15可得基于SOGI的二阶自适应滤波器输入-输出的传递函数为

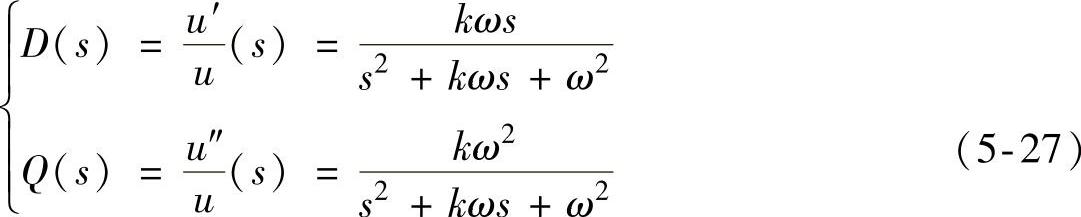
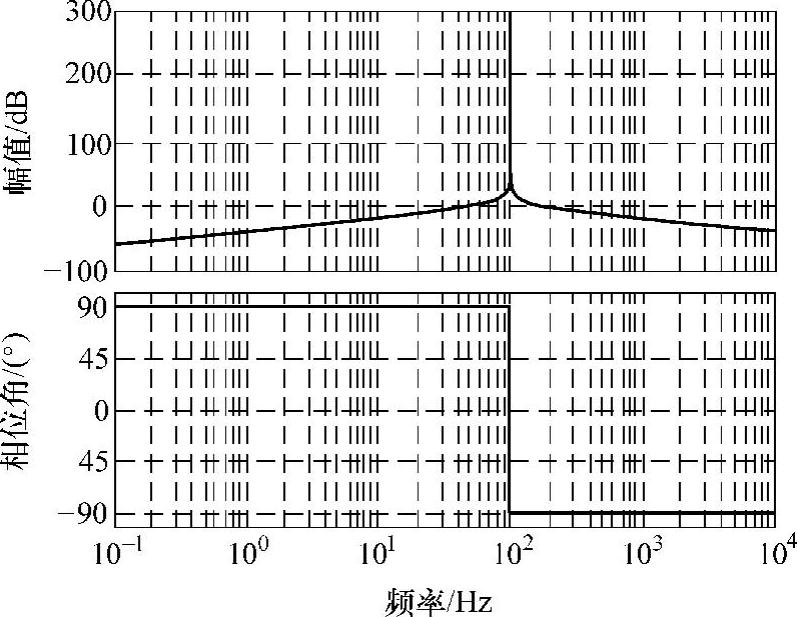
图5-16 SOGI幅频和相频特性

其幅频和相频特性曲线如图5-17所示。可见，图5-15所设计的滤波器本质上也是带通滤波器，与SOGI相比，其频带被延展，对输入信号频率波动的鲁棒性变强，当参数ω一定时，其带宽仅与k有关；对于输出u″而言，在带通滤波的同时，该滤波器还可以实现中心频率信号的-90°相移，呈现相移滤波的特性，由式（5-21）可知，若输入信号为两相静止坐标系下的电压分量u_αβ，则应用该滤波器，且将滤波后的信号经适当运算可实现u_αβ的正负序分量分离。

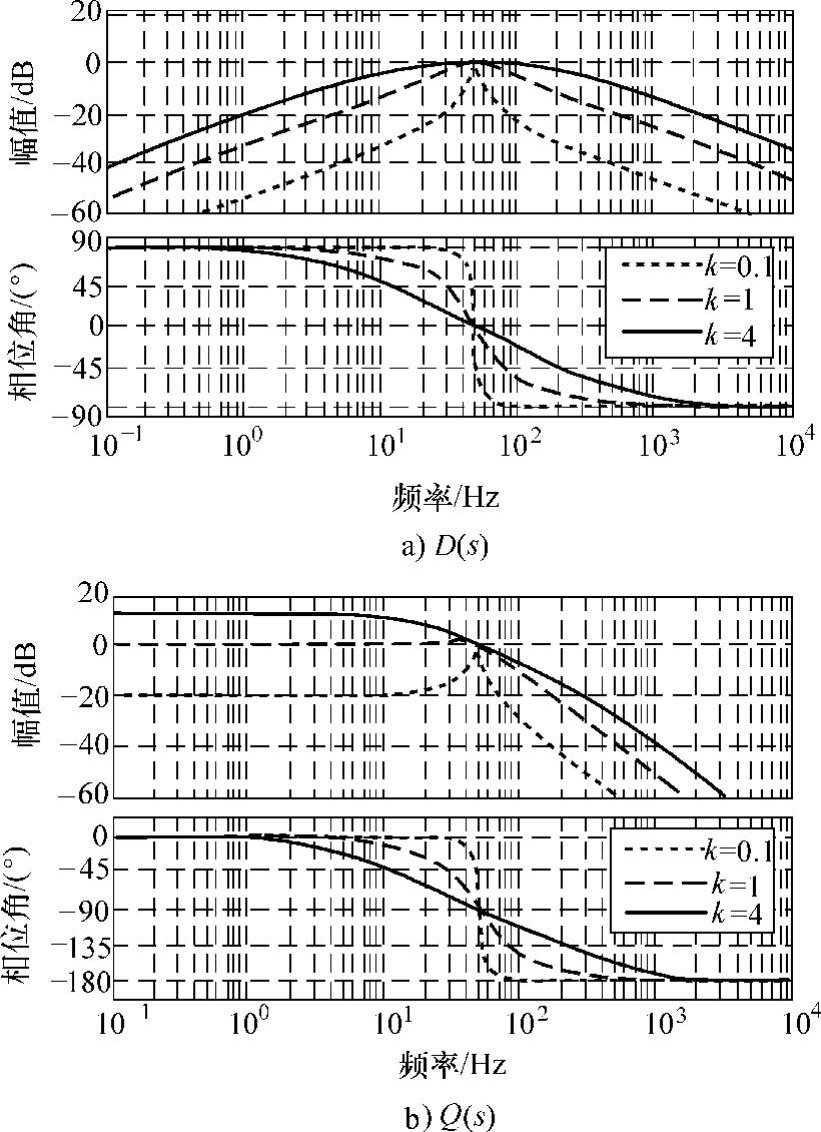
图5-17 基于SOGI二阶滤波器的输入输出特性

除了上述滤波器以外，还有其他结构的滤波器，比例正弦信号积分器（Por-tional-Sinusoidal Signal Integrator，P-SSI）^[23]、三阶自适应陷波滤波器（Adaptive Notch Filter，ANF）^[24]等也可应用于正负序电压分量的检测中。一方面，从本质上来看，这些滤波器都是与基于静止坐标系或旋转坐标系下的PD结合使用的，其特性与前面提到的低通或带通滤波器相似；另一方面，在复杂度和滤波性能方面，上述滤波器并不具有更大的优势，因而本书不再进行详述。

基于以上PD和LF环节，在静止和同步旋转坐标系中可实现不同结构的锁相环。