光伏发电系统最大功率点跟踪控制优化

光伏发电系统中，光伏电池的利用率除了与光伏电池的内部特性有关外，还受使用环境如辐射强度、负载和温度等因素的影响。在不同的外界条件下，光伏电池可运行在不同且唯一的最大功率点（Maximum Power Point，MPP）上。对于光伏发电系统来说，应当寻求光伏电池的最优工作状态，以最大限度地将光能转化为电能。利用控制手段实现光伏电池输出最大功率的技术被称为最大功率点跟踪（Maximum Power Point Tracking，MPPT）技术^[10，11]。传统的MPPT方法依据判断方法和准则的不同可分为开环和闭环MPPT方法^[12]。

开环MPPT方法根据外界温度、光照和负载变化对光伏电池输出特性曲线的影响开环控制光伏电池输出的电压和电流^[13]。这一类方法简便易行，但对光伏电池的输出特性依赖性较强、效率较低，实际中常和闭环MPPT方法配合使用。闭环MPPT方法通过对光伏电池输出电压和电流值的实时测量，采用闭环控制方法来实现MPPT，使用最广泛的自寻优类算法即属于闭环MPPT方法。典型的自寻优类MPPT算法有扰动观测法和电导增量法。

4.2.1.1 开环MPPT控制

基于光伏电池的输出特性曲线，通过简单的开环控制来实现MPPT，主要包括定电压跟踪法^[14]、短路电流比例系数法^[14]和插值计算法^[15]。

1.定电压跟踪法

如图4-2b所示，当辐射强度大于一定值且温度变化较小时，光伏电池输出P-U曲线上最大功率点的电压值几乎恒定。控制光伏电池输出电压为该电压值时，光伏电池将获得近似的最大功率输出，这种MPPT控制称为定电压跟踪法。进一步研究发现，光伏电池的最大功率点电压U_mpp与光伏电池开路电压U_oc之间存在近似的线性关系，即

U_mpp≈k₁U_oc （4-12）

式中，系数k₁取决于光伏电池特性，一般k₁取值约为0.8。根据式（4-12）控制光伏电池输出电压即可实现MPPT。

定电压跟踪法控制简单快速，但由于忽略了温度对光伏电池输出电压的影响，因此温差越大，最大功率点的跟踪误差也就越大。

2.短路电流比例系数法

由图4-2a可知，当辐射强度大于一定值且温度变化较小时，光伏电池的输出U-I曲线上最大功率点电流I_mpp与光伏电池短路电流I_sc也存在近似的线性关系，即

I_mpp≈k₂I_sc （4-13）

式中，系数k₂取决于光伏电池特性，一般k₂取值也约为0.8。根据式（4-13）控制光伏电池输出电压也可实现MPPT。

定电压跟踪法和短路电流比例系数法的主要优点就是控制简单且易于实现。但由于式（4-12）和式（4-13）是近似公式，所以光伏电池并非工作在真正的最大功率点上，常常需要和其他的MPPT算法配合使用，以获得较快的跟踪速度和较高的跟踪准确度。

3.插值计算法

如图4-7所示，采用定电压跟踪法时，假设初始工作点电压为U₁，此时光伏电池工作在最大功率点P₁；若外部条件变化，最大功率点变为P₂，但由于光伏电池输出电压还是U₁，其输出功率从原先的P₁变为P₁′，远离P₂，显然该方法下，外部条件变化时，光伏电池的实际运行点偏离理论最大功率点。

针对上述情况，基于有限次采样值，利用插值算法构建光伏电池的P-U曲线，通过求取该P-U曲线的极值点来近似得到光伏电池的最大功率点。

4.2.1.2 闭环MPPT控制

闭环MPPT方法通过对光伏电池输出电压和电流值的实时测量与闭环控制来实现MPPT，最常用的是扰动观察法。

1.扰动观测法[16，17]

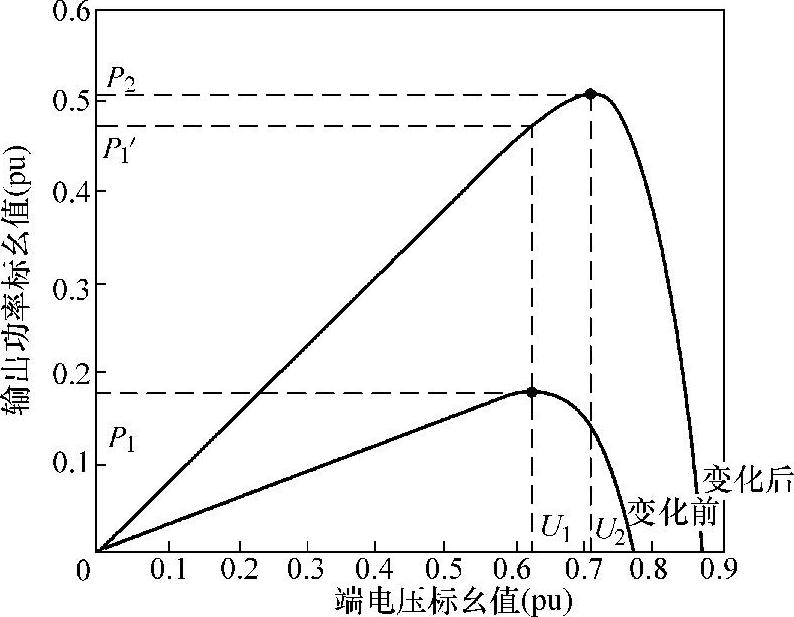
图4-7 外部条件变化时工作点变化情况示意(www.xing528.com)

扰动观测法（Perturbation and Observation method，P&O）是实现MPPT最常用的自寻优类方法之一。其基本思想是：在光伏电池的输出电压（或电流）上人为增加扰动，观测光伏电池输出功率的变化，根据功率变化趋势连续改变电压（或电流）的扰动方向，使光伏电池最终工作于最大功率点。

正常条件下，光伏电池的P-U曲线只存在唯一的最大功率点，这一特点为采用扰动观测法寻找最大功率点提供了条件。扰动观测法本质上采用了步进搜索的思路，即从起始状态开始，每次对输入信号做有限变化，然后测量由于输入信号变化而引起的输出变化，根据输出变化方向，控制输入扰动的变化方向，最终实现自寻最优控制。

为讨论方便，假定辐射光强度、温度等环境条件不变，并设U、I为上一次光伏电池的电压、电流检测值，P为对应的输出功率，U₁、I₁为当前光伏电池的电压、电流检测值，P₁为对应的输出功率，ΔU为电压调整步长，ΔP为电压调整前后的输出功率差，ΔP=P₁-P。图4-8显示了扰动观测法的MPPT过程，具体描述如下：

1）当增大参考电压U（U₁=U+ΔU）时，若P₁>P，表明当前工作点位于最大功率点的左侧，此时系统应保持增大参考电压的扰动方式，即U₂=U₁+ΔU，其中U₂为第二次调整后的电压值，如图4-8a所示；

2）当增大参考电压U时，若P₁﹤P时，表明当前工作点位于最大功率点的右侧，此时系统应采用减小参考电压的扰动方式，即U₂=U₁-ΔU，如图4-8b所示；

3）当减小参考电压U时，若P₁﹥P时，表明工作点位于最大功率点的右侧，系统应保持减小参考电压的扰动方式，即U₂=U₁-ΔU，如图4-8c所示；

4）当减小参考电压U时，若P₁﹤P时，表明工作点位于最大功率点的左侧，此时系统应采用增大参考电压的扰动方式，即U₂=U₁+ΔU，如图4-8d所示。

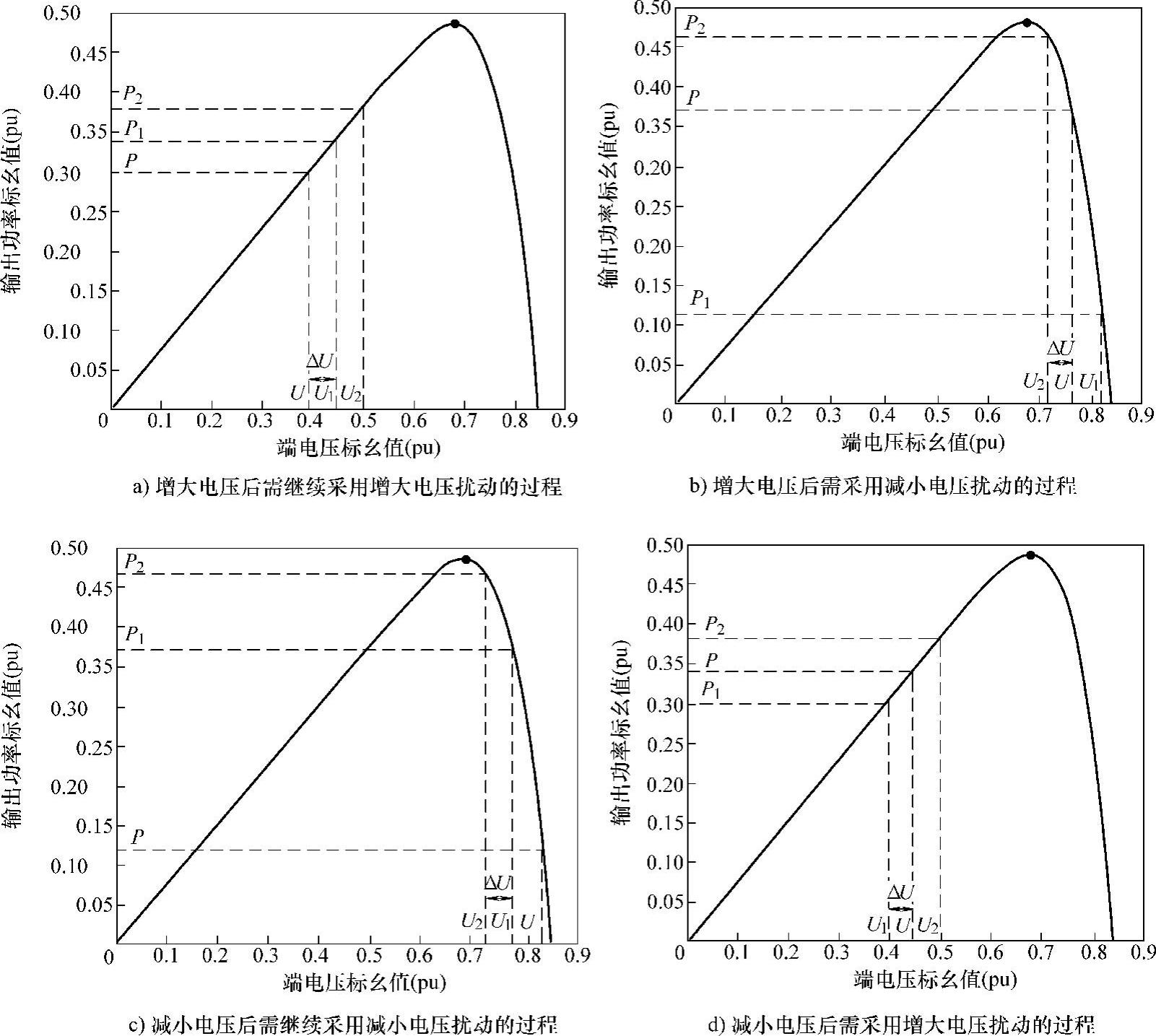
图4-8 扰动观测法MPPT过程示意

可见，扰动观测法可按图4-8所示的过程反复进行输出电压扰动，并使其不断变化，从而使光伏电池输出功率不断增加，直到工作在最大功率点。由以上分析可知，扰动观测法控制概念清晰、简单，被测参数少，因此普遍应用于实际光伏系统的MPPT控制中。值得注意的是，在扰动观测法中，电压初始值及扰动电压步长对跟踪准确度和速度有较大影响。定步长扰动观测法（扰动电压恒定）存在振荡和误判问题，使系统不能准确跟踪最大功率点，会造成能量损失，因此需要对其进行改进。一般的改进方法包括：采用变步长扰动电压，在减小振荡的同时，可使系统更快地跟踪最大功率点^[16]；采用功率预测的扰动观测法，可有效解决外部环境剧烈变化时所引起的MPPT误判问题^[17]；采用滞环比较的扰动观测法，可克服最大功率点跟踪过程中的振荡和误判^[18]。

2.电导增量法^[12]

为进一步提高MPPT算法的跟踪准确度，可采用光伏电池的电导和电导变化率的变化关系作为搜索判据，该方法也称电导增量（Incremental Conductance INC）法。图4-9所示为光伏电池P-U特性曲线及dP/dU_pv的变化特征。

由光伏电池输出功率-电压关系，对光伏电池输出电压U_pv求导，可得

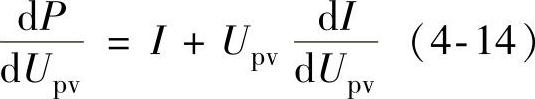
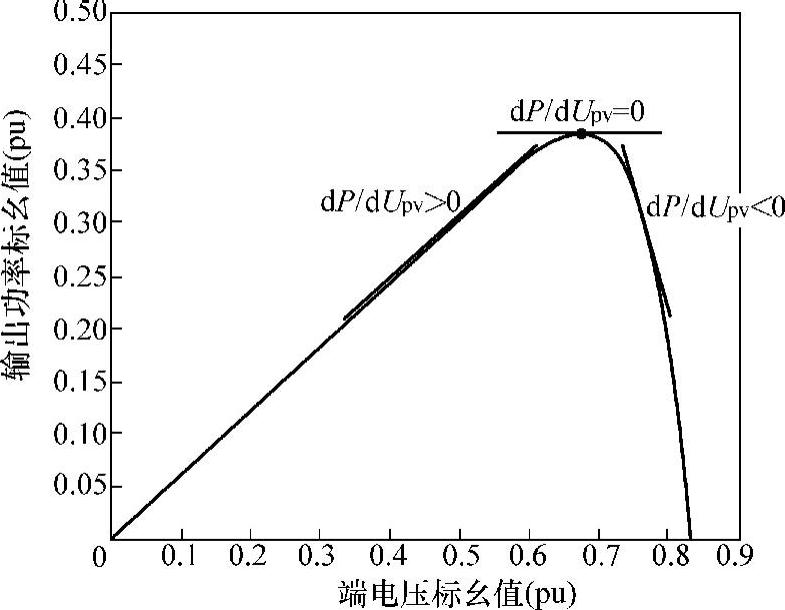
图4-9 光伏电池P-U特性的dP/dU_pv变化特征

由图4-9可知，当dP/dU_pv=0时，光伏电池的输出功率达到最大。由式（4-14）可推导出光伏电池工作于最大功率点时需满足以下关系：

采用电导增量（INC）法进行最大功率点跟踪的判据如下：

电导增量法的主要优点是MPPT的控制稳定度高，当外部环境参数变化时，系统能平稳地追踪其变化，与光伏电池的特性及参数无关。然而，电导增量法对控制系统要求相对较高，电压初始化参数对跟踪性能有较大影响，若设置不当，该方法容易产生振荡和误判的问题，基于变步长的电导增量法^[19-21]对于抑制振荡具有较好的效果，基于功率预测的电导增量法[18]对解决外部环境剧烈变化时的误判问题比较有效。