光伏电池的数学模型优化方案

光伏电池本质为大面积的平面二极管，其工作原理可以用图4-1的单二极管等效电路来描述[1]。图中R_L是光伏电池的外接负载，负载电压（光伏电池的输出电压）为U_pv，负载电流（光伏电池的输出电流）为I。

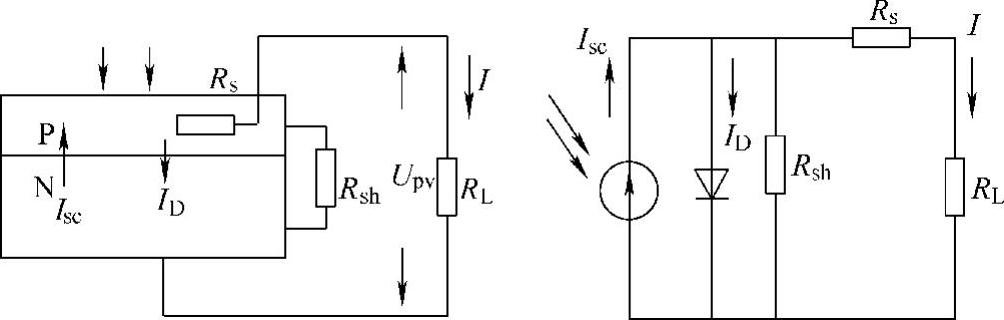
图4-1 光伏电池的单二极管等效电路

图中，I_sc代表光子在光伏电池中激发的电流，其值取决于光照强度、电池面积和本体温度T。其中，I_sc与入射光的辐照度成正比，温度升高时，I_sc会略有上升。一般来说，1cm²硅光伏电池在标准测试条件下的I_sc值约为16～30mA，温度每升高1℃，I_sc值上升78μA。I_D（二极管电流）为通过PN结的总扩散电流，其方向与I_sc相反，表达式为

由式（4-1）可知，总扩散电流的大小与光伏电池的电动势E和温度T等有关。式中，q为电子电荷量，q=1.6×10^-19 C；K为玻耳兹曼常数，K=1.38×10^-23 J/K；A为光伏电池常数因子（正偏电压较大时，A值可取1，正偏电压较小时，其值可取为2）。

I_D0为无光照时光伏电池的饱和电流：

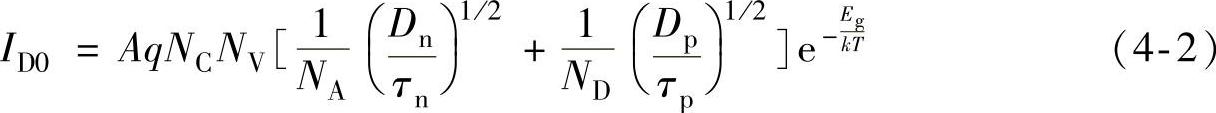
式中，A为PN结结面积；N_C、N_V为导带和价带的有效态密度；N_A、N_D为受主杂质和施主杂质浓度；D_n、D_p为电子和空穴的扩散系数；τ_n、τ_p为电子和空穴的少子寿命；E_g为半导体材料的带隙。

根据图4-1，可得到负载电流I_L为

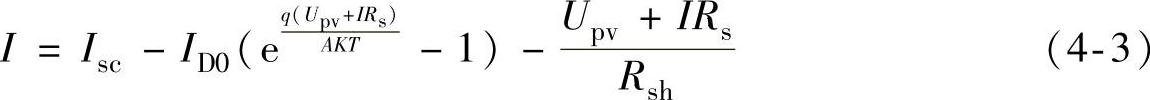
式中，R_s为串联电阻，它主要是由电池体电阻、表面电阻、电极导体电阻、电极与硅表面的接触电阻所组成；R_sh为旁漏电阻，它是由于硅片的边缘不清洁或体内的缺陷引起的。

正常光照条件下，光伏电池的输出功率特性曲线是以最大功率点为极值的单峰值曲线，图4-1和式（4-3）给出的单二极管模型可以较准确地描述其工作特性。光伏电池中，串联电阻R_s一般很小，旁漏电阻R_sh很大，在进行理想电路计算时，上述电阻均可忽略不计，由此可得理想光伏电池特性的表达式为

由式（4-4）可得

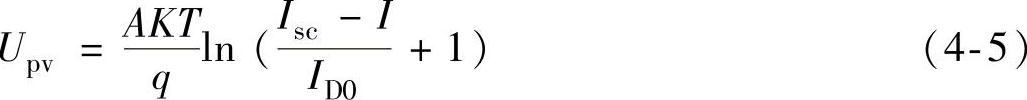(https://www.xing528.com)

式（4-4）和式（4-5）忽略了R_s和R_sh的影响，与真实光伏电池输出有一定偏差，但仍可以体现照度和温度对光伏电池输出的影响。由式（4-4）可知，外电路短路时（短路试验，R_L=0），输出电流I=I_sc。

外电路开路时（开路试验，R_L→∞），电池两端电压为开路电压U_oc。由式（4-5）可计算出光伏电池的开路电压为

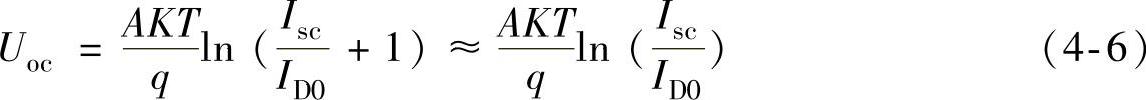
U_oc与太阳光照度有关，而与光伏电池面积无关。当入射光照度变化时，光伏电池的开路电压与入射光谱辐射照度的对数成正比。当温度升高时，光伏电池的开路电压值将下降。一般，温度每上升1℃，U_oc值下降约2～3mV。在1000W/m²的辐射照度下，硅光伏电池的开路电压为450～600mV，最高可达690mV。

U-I的关系即为光伏电池的外特性，也称输出特性，该特性是设计光伏发电系统的重要基础，其中，辐射照度和温度是确定光伏电池输出特性的两个重要参数[2]。温度固定时改变照度，或者固定辐射照度时改变温度，可得到光伏电池输出随负载变化的两族特性曲线，分别如图4-2、图4-3所示。

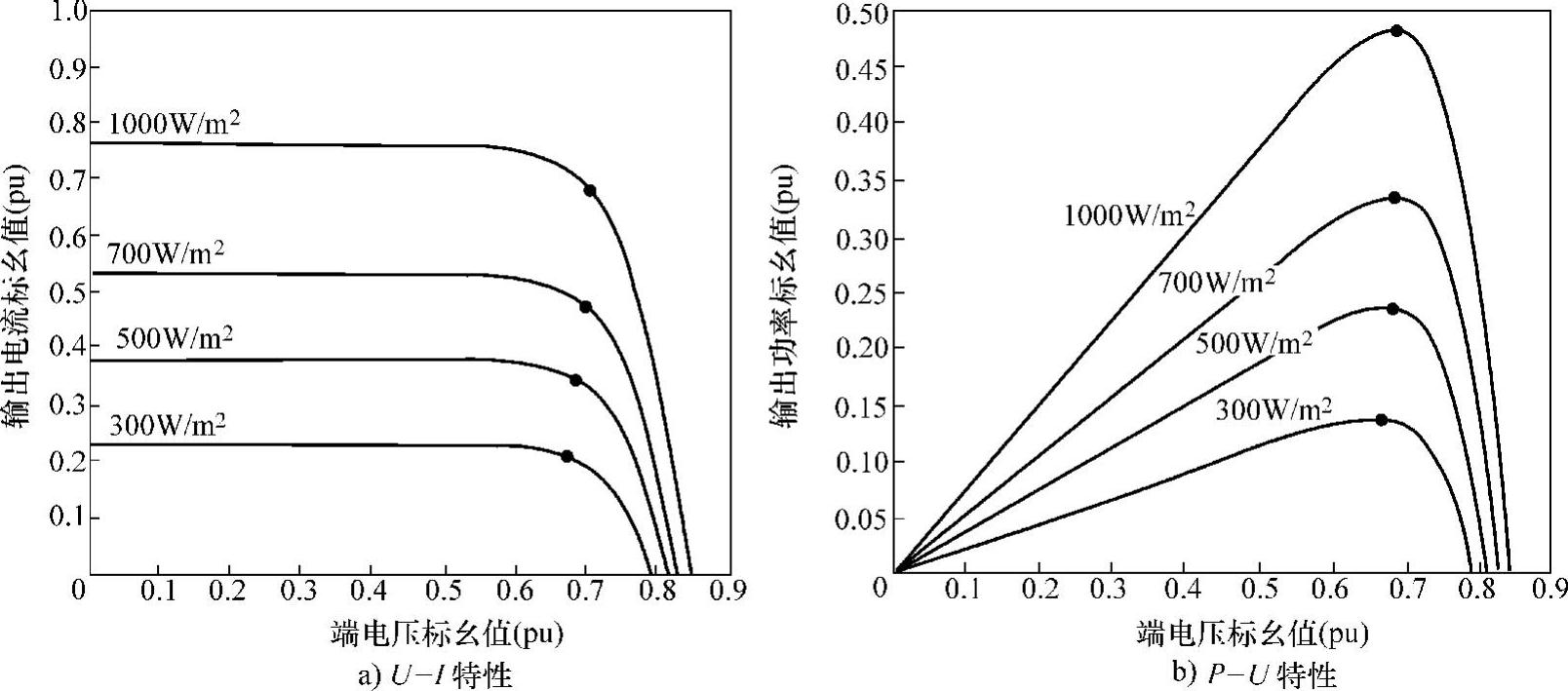
图4-2 相同温度而不同辐射照度条件下光伏电池特性

图4-2为温度一定条件下，光伏电池的输出随辐射照度和负载变化的U-I和P-U曲线族。由图4-2a可见，开路电压U_oc随辐射照度的变化并不明显，短路电流I_sc受辐射照度影响较大。由图4-2b可知，辐射照度和温度一定时，光伏电池（组件）输出功率并不恒定，随着光伏电池电压的上升，电池输出功率亦逐渐增加；光伏电池电压达到一定值时，其输出功率可达最大；此时进一步增加光伏电池输出电压，其输出功率将逐渐减少，零功率输出对应的光伏电池输出电压即为其开路电压U_oc。图中，输出功率最大的点，也称为最大功率点；该点所对应的光伏电池电压，称为最大功率点电压U_m，对应电流，称为最大功率点电流I_m，其功率称为最大功率P_m。辐射照度变化时，最大功率P_m也随之明显变化。

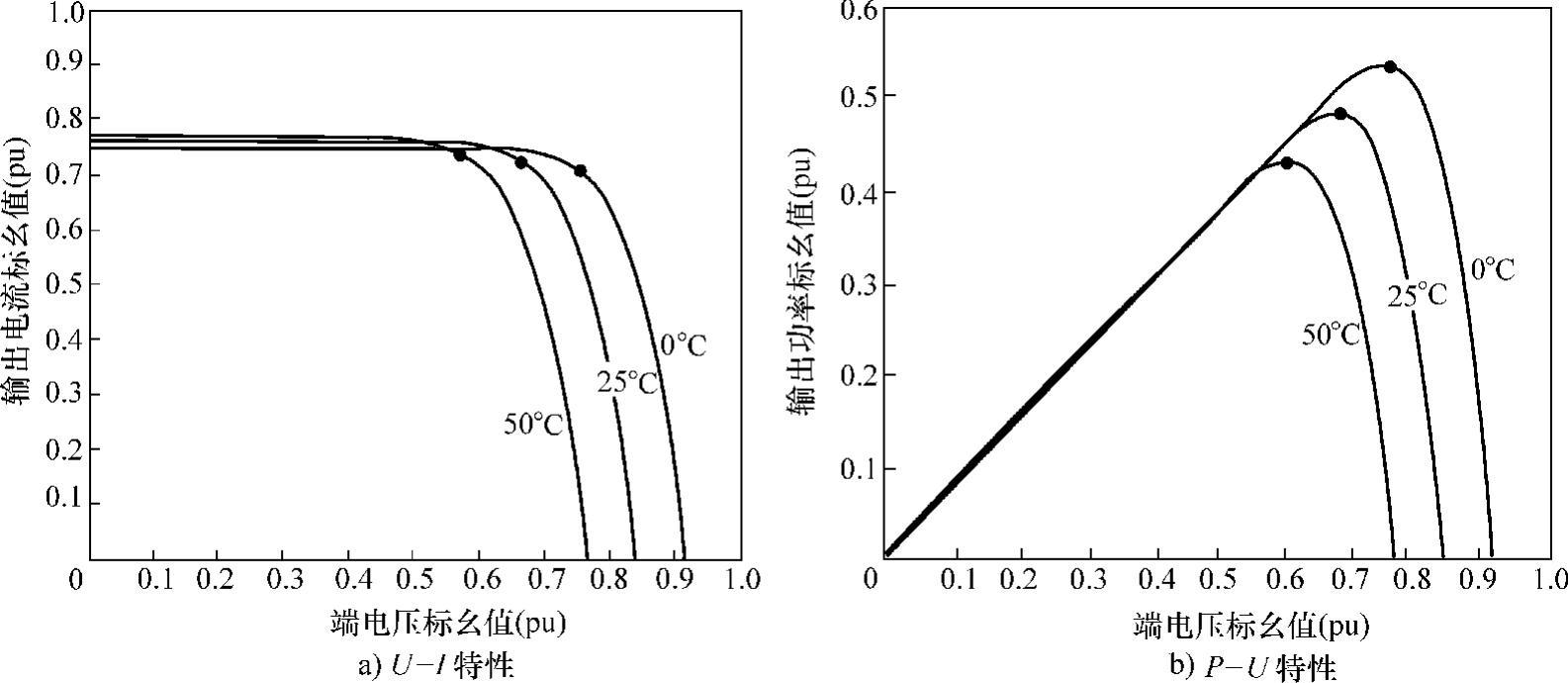
图4-3 相同辐射照度而不同温度条件下光伏电池特性

图4-3为保持辐射照度不变，光伏电池的输出随电池温度和负载变化的U-I和P-U曲线族。由该曲线族可见，开路电压U_oc随温度线性变化，短路电流I_sc随温度变化较小。最大功率点功率P_m受温度变化影响较大。值得注意的是，本节所讨论的光伏电池温度应为光伏电池本体温度而非环境温度。一般，光伏电池温度与环境温度有如下关系^[3]：

T=T_air+kS （4-7）

式中，T是光伏电池温度（℃）；T_air为环境温度（℃）；S为辐射照度（W/m²）；k为系数（℃·m²），可在实验室测得。

上述特性曲线表征光伏电池随辐射照度和温度变化的趋势。可见，光伏电池既非恒流源，也非恒压源，而是非线性直流电源。光伏电池提供的功率取决于阳光所提供的能量，因此不可能为负载提供无限大的功率。