机械系统的数学模型优化

3.1.1.1 风力机^[1-6]

风力机是风力发电系统捕获风能的首要部件，它将叶片扫掠面积内的空气的动能转换为机械能，相当于传统发电系统的原动机。目前，兆瓦级风电机组通常采用三叶片、水平轴结构的风力机。

由空气动力学原理可知，风力机输入功率（气流功率）为

式中，ρ为空气密度；S为风力机叶片的扫掠面积；v为风速。

气流功率不会完全被风力机吸收并转换为机械能，两者之间的比例关系即为风能利用系数（也称为风力机的功率系数），即

因此，风力机捕获的风能为

需要注意的是，风能利用系数C_p不是常数，其值与风速、风力机转速等都有关系。根据贝茨理论，C_p的理论上限为0.593，当前技术条件下，现代风力机的C_p在0.2～0.5范围内。对于风轮直径为82m、风能利用系数C_p=0.36的三叶片风力机，当风速为12m/s、空气密度ρ=1.225kg/m³时，其捕获功率为2MW。

基于空气动力学的理论分析和风洞实验的测试结果均表明，风能利用系数C_p是风速、风力机转速和叶片桨距角的非线性函数，即

C_p=C_p（Ω_WT，v，β） （3-4）

式中，Ω_WT为风力机角速度；β为风力机桨距角。

进一步，可将风速和风力机转速的影响统一用叶尖速比的影响来描述，即定义叶尖线速度与风速之比为叶尖速度比

式中，R为风力机叶片扫掠半径。

则C_p可以简化描述为

C_p=C_p（λ，β） （3-6）

上式函数关系依赖于风力机的空气动力学特性，典型曲线关系如图3-1所示。由图可知：

1）桨距角β一定时，风能利用系数C_p随叶尖速度比λ先增大后减小，并存在一个最大值，该最大值意味着此时风力机转速与风速相匹配，风能利用率最高。该最大值对应的叶尖速度比即为最优叶尖速度比λ_opt。若能控制风力机转速以保证其叶尖速度比λ为最佳值λ_opt，即可实现风电系统的最大风能捕获；

2）总体来说，风能利用系数C_p随桨距角β的增加而减小，可通过调节桨距角以减少风能捕获量，因此现代风力机常利用变桨距角技术限制高风速时风力机的捕获功率。

图3-1所示风能利用系数的数学模型可由高阶多项式[4]或超越函数[5]来模拟，对于不同厂商的风力机，上述数学模型中的参数有所不同；一般，风力机厂商在风力机出厂后会提供相应风力机的实测功率-转速曲线，因而风能利用系数的数学模型也可根据厂商提供的曲线，采用插值的方法模拟得到^[6]。

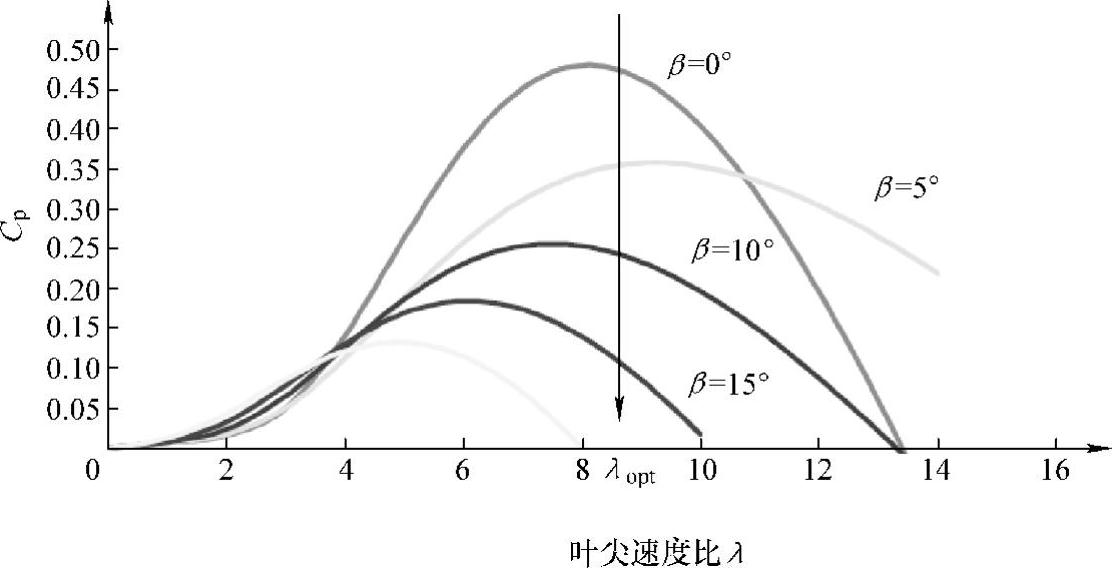
图3-1 风力机空气动力学特性典型曲线

3.1.1.2 传动链^[7-9](www.xing528.com)

风电系统的传动链一般由风力机、低速轴、齿轮箱、高速轴和发电机转子组成，在直驱结构的风电系统中，由于采用了多级低速发电机，风力机和发电机同轴相连，不存在高低速轴和齿轮箱。

风电系统传动链由多个机械部件同轴相连，由于不同机械部件的转动惯量不尽相同，实际风电系统的轴系具有一定柔性。采用齿轮箱耦合的风力发电系统，由于风力机和发电机的惯量相差较大，传动链柔性更为明显；直驱结构的风电系统，发电机采用多极结构，以实现低速运行，由于发电机传动轴的等效刚性与其极对数成反比，传动轴的柔性也较大^[10]。因此，在研究大型变速风电系统时，传动链的动态不可忽略，一般其动态模型可由多质量体的弹簧模型来简单描述。

将风力机、齿轮箱和发电机转子分别看作三个质量体，典型风电系统传动链可由三质量体-弹簧模型来描述，如图3-2所示。

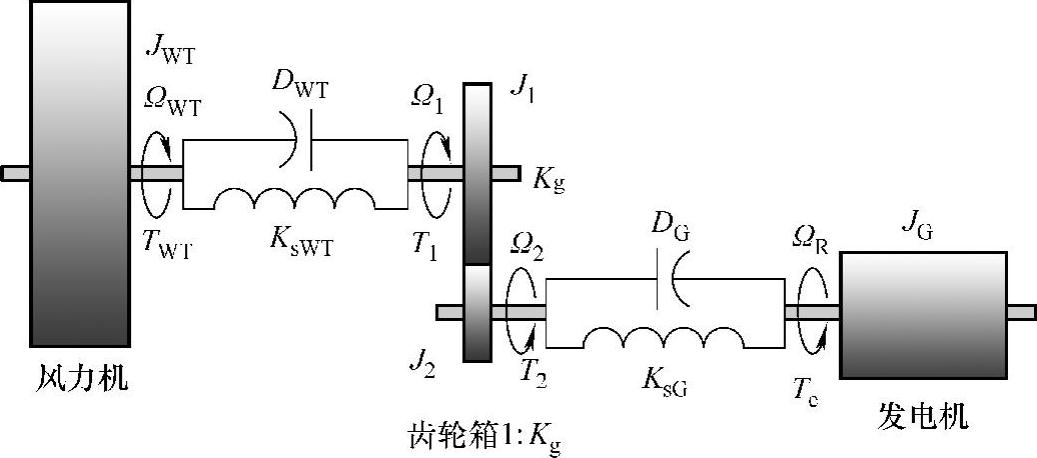
图3-2 三质量体-弹簧模型

发电机惯例下的传动链数学模型为

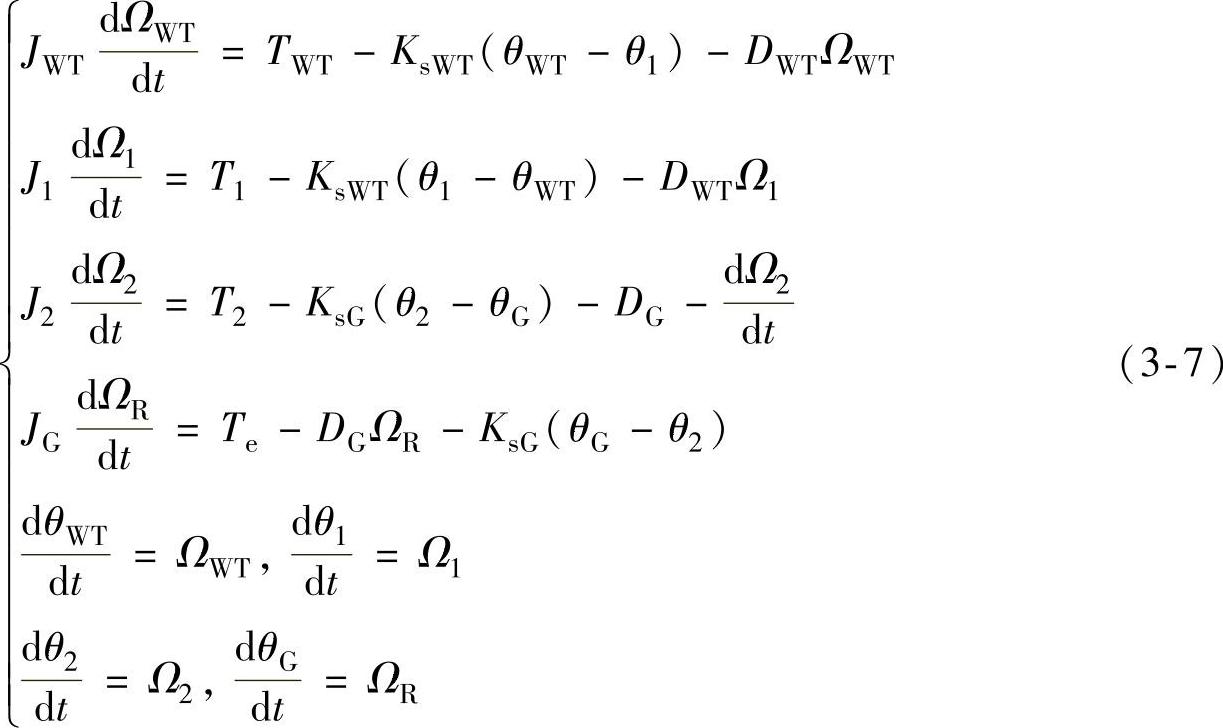
式中，J_WT、JG分别为风力机的风轮和发电机转子转动惯量；Ω_R为发电机机械角速度；T_WT、T_e为风力机机械转矩和发电机电磁转矩；T₁，T₂为齿轮箱输入和输出转矩；D_WT，D_G为风力机和发电机的阻尼系数；K_sWT，K_sG为风机侧和发电机侧齿轮箱轴的刚性系数；θ_WT、θ₁、θ₂和θ_G分别为风力机、齿轮箱低速侧、齿轮箱高速侧和发电机的位置角；J₁、J₂分别为齿轮箱低速轴和高速轴的转动惯量；Ω₁，Ω2分别为齿轮箱低速轴和高速轴的机械角速度，Ω₂=K_gΩ₁，K_g为齿轮箱变比。

若忽略风力机、低速轴和齿轮箱轴系的柔性，将其转动惯量及刚度折算到高速轴侧，则上述三质量体-弹簧模型可简化为两质量体-弹簧模型，如图3-3所示^[10]。

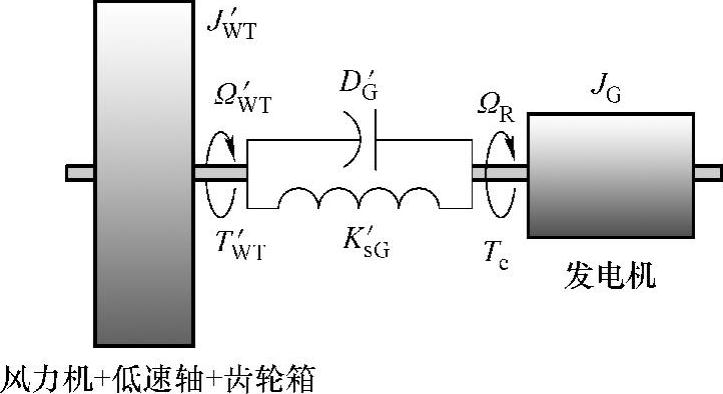
图3-3 两质量体-弹簧模型

两质量体-弹簧系统的动态模型为

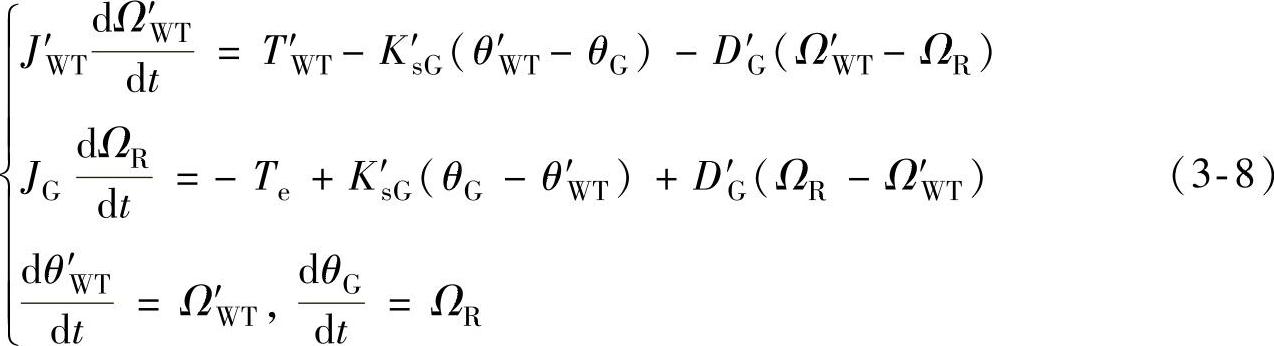
式中，J′_WT为风力机等效转子惯量，J_W′_T=J_WT/K²_g；Ω′_WT为风力机等效机械转速，Ω_W′_T=K_gΩ_WT；T_W′_T为风力机等效机械转矩，T_W′_T=T_WT/K²_g；K_s′_G为传动轴的等效刚性系数，1/K_s′_G=K²_g/K_sWT+1/K_sG；θ_W′_T为风力机轴的等效扭角；D_G′为发电机等效阻尼系数，1/D_G′=K²_g/D_WT+1/D_G。

进一步，忽略高速轴和发电机转子轴系的柔性，将传动链所有轴系组件的转动惯量和刚度折算到发电机转子侧，可得单质量体-弹簧模型，如图3-4所示。

忽略机械阻尼后，传动链的数学模型为

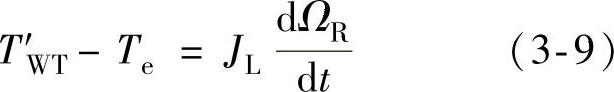
式中，J_L为等效风电机组风轮转动惯量，J_L=J_G+J′_WT。

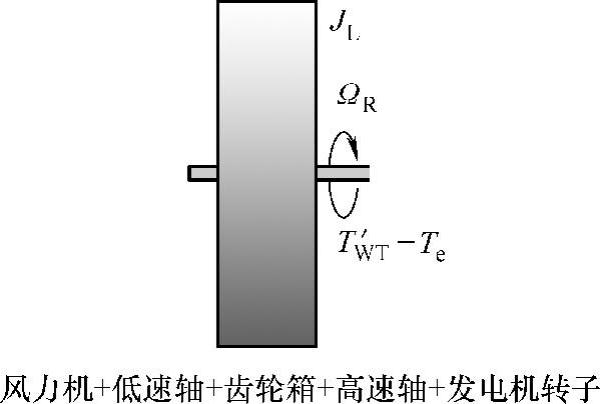
图3-4 单质量体-弹簧模型

在上述数学模型中，单质量体模型最为简单，常用于研究风电系统的功率控制和动态响应等基本特性；三质量体模型最为准确，但较复杂，因而使用较少；两质量体模型复杂度和准确度都适中，常用于分析电网电压故障下风电场和电力系统的暂态稳定性，在此类研究中，采用两质量体模型得到的研究结果与三质量体模型非常接近^[11]。

3.1.1.3 变桨距系统

大型风电系统的变桨距机构一般采用液压或电动方式驱动。电动变桨距机构结构简单、维护量小，在当前风电系统中更为常见。对于传统风力机，其所有叶片均通过一套变桨距机构同时调节；最新的风力机则设计为各叶片可通过各自变桨距机构单独调节，其应用更加灵活。

由于叶片重量较大，变桨距机构的调节速度有限，一般其最大调节率为10°/s，叶片桨距角的变化范围通常为0～30°，其数学模型可由具有饱和环节的一阶延时系统来表征^[12]。桨距角调节时，为抑制噪声干扰和避免频繁动作，控制器中通常会设计调节死区，一般当桨距角指令变化速率小于0.1°/s时，变桨距机构不予响应^[13]。