分析试验梁开裂弯矩情况

试验梁在受到外荷载时，在裂缝出现之前，受拉区混凝土与钢筋共同受力，由于混凝土具有不均匀性，所以实际上混凝土梁各截面的抗拉强度是有差异的，随着荷载的不断增加，在混凝土试验梁纯弯段截面出现裂缝，此时的弯矩看作开裂弯矩。

1.试验结果与分析

为了便于分析，在此引入无量纲系数αcr，以消除截面尺寸及基体强度的影响。

式中 αcr——开裂弯矩相对值；

Mtcr——开裂弯矩试验值，kN·m；

b——试验梁宽度，mm；

h0——试验梁有效高度，mm；

ftk——再生混凝土梁抗拉强度，MPa。

开裂弯矩试验数据见表10.5。

表10.5　试验梁开裂弯矩

根据表10.5中数据绘制出开裂弯矩相对值随着再生粗骨料取代率的变化情况，如图10.7所示。从图10.6中可以看出：随着再生粗骨料取代率的增大，开裂弯矩相对值呈逐渐减小趋势。再生粗骨料取代率为40%、70%、100%的试验梁开裂弯矩相对值比普通混凝土分别降低了4.4%、6.7%、10.6%，这说明粗骨料的掺入使得混凝土的抗裂性能减弱，并且随着掺量的增加，减弱的幅度增大。

2.开裂弯矩试验值与理论计算值对比

按照《混凝土结构设计规范》 （GB 50010—2002）中的方法和公式计算开裂弯矩的计算值，计算出的开裂弯矩试验值见表10.6。(www.xing528.com)

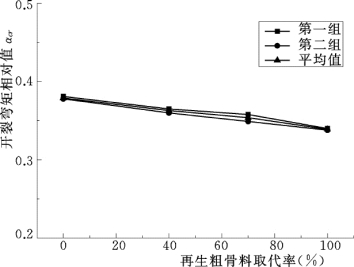
图10.7　试验梁开裂弯矩相对值随再生粗骨料取代率的变化

表10.6　开裂弯矩试验值与计算值

注 Mtcr为开裂弯矩计算值；Mc1cr为开裂弯矩计算值；Mc2cr为开裂弯矩调整值。

由表10.6可以得出：Mtcr/Mc1cr平均值为0.941，标准差为0.049，变异系数为0.052，开裂弯矩计算值与试验值比较接近，标准差和变异系数都很小，普通混凝土梁Mtcr/Mc1cr的值分别为1.021和1.010，接近1且大于1，说明普通混凝土开裂弯矩试验值与理论计算值符合较好。从表10.6中看出再生混凝土梁的Mtcr/Mc1cr均小于1，说明现行《混凝土结构设计规范》（GB50010—2002）中开裂弯矩计算公式已不适用于再生混凝土梁。

为更好地推算再生混凝土梁的开裂弯矩，需要对再生混凝土梁开裂弯矩计算公式进行调整，拟采用再生混凝土试验梁与普通混凝土梁开裂弯矩之比为修正系数，调整值为理论计算值乘以修正系数，从表10.6中可看出采用调整后的Mtcr/Mc2cr值在1左右，计算可得出Mtcr/Mc2cr平均值为1.059，标准差为0.043，变异系数为0.041，开裂弯矩试验值与计算值较好符合。对表10.6中的数据进行回归分析，得到再生混凝土梁开裂弯矩修正系数与再生粗骨料取代率的关系，如图10.8所示。

图10.8　修正系数与再生粗骨料取代率的关系图

由图10.8可以看出再生混凝土梁开裂弯矩修正系数与再生粗骨料取代率总体上呈线性关系，其关系式为

式中 η——开裂弯矩计算值修正系数；

ρr——再生粗骨料取代率。

由于试验数据有限，该关系式有待验证。