数值模拟结果及分析

通过圆柱体和立方体两种试件及再生骨料掺量为0、40%、70%和100%的四种工况，进行有限元数值模拟，得到如下结果。

（1）圆柱体试件单轴压缩损伤破坏过程的模拟结果及分析。

中心纵剖面为y＝50mm，取y＝20mm、y＝40mm、y＝60mm和y＝70mm四个纵剖面。当位移加载到uz＝4mm时的开裂应变分布如图9.18所示，从图9.18（a）开裂应变分布图可以看出底部的应变较大，上部的应变较小，而图9.18（d）正好与图9.18（a）分布结果相反。从图9.18（a）～ （d）整体效果上看，试件的破坏形态属于斜截面破坏，或者从中间两个纵剖面的开裂应变分布图亦可看出试件的破坏形态属于斜截面破坏，与试验室的试验规律相同。

中心纵剖面为y＝50mm，当位移荷载依次为uz＝1.15mm、uz＝1.55mm、uz＝1.95mm、uz＝2.19mm、uz＝3.12mm、uz＝3.67mm、uz＝3.87mm和uz＝4mm时，该剖面开裂应变分布的变化过程如图9.19所示。显然从该系列图可以看出随着位移荷载的逐步加大，损伤区域从斜截面逐步向两侧发展，与实际情况吻合。

图9.18　位移加载到uz＝4mm时纵剖面的开裂应变分布图

图9.19　中间纵剖面开裂应变分布的变化过程图

（2）立方体试件单轴压缩损伤破坏过程的模拟结果及分析。

中心纵剖面为y＝75mm，中心横截面为z＝75mm，取z＝75mm、z＝100mm、z＝115mm和z＝125mm四个横截面，取y＝75mm、y＝105mm、y＝135mm三个纵剖面，当位移加载到uz＝3mm时的开裂应变分布如图9.20～图9.23所示。从图9.20～图9.23的开裂应变分布图可以看出损伤区域集中出现在周边，且横截面四角损伤区域由中部往顶部和底部逐步变小。从几个纵剖面的损伤区域分布 （图9.23）可以看出再生混凝土试件在单轴压缩（考虑加载的摩擦效应）作用下呈现双倒三角剥离，符合试验规律。

图9.20　压缩试件破坏时的开裂应变分布图

图9.21　破坏时横截面z＝75mm的开裂应变分布图

图9.22　破坏时各横截面的开裂应变分布图

图9.23　破坏时各纵剖面的开裂应变分布图

当位移荷载依次为uz＝0.86mm、uz＝1.31mm、uz＝1.64mm、uz＝2.34mm、uz＝2.83mm和uz＝3mm时，纵剖面y＝135mm的开裂应变分布的变化过程如图9.24所示，显然从该系列图中可以看出，随着位移荷载的逐步加大，损伤区域从两侧逐步向中心呈倒三角发展，与实际情况吻合。

图9.24　纵剖面y＝135mm开裂应变分布的变化过程图

（3）单轴压缩损伤破坏过程的应力—应变关系提取及分析。(www.xing528.com)

从模拟结果各加载步提取试件中部 （圆柱体z为80～100mm，立方体z为60～90mm）节点的压缩应力，然后取其平均值作为整体试件各加载步的压缩应力，取加载步的位移荷载除以试件高度作为相应加载步的压缩应变，绘出压缩应力—应变关系曲线，如图9.25、图9.26所示。从这两图可以看出，圆柱体试件的峰值强度比立方体试件低，反映试件的尺寸效应。与第4章试验数据相结合绘制出不同再生骨料掺量下的应力—应变关系图如图9.27～图9.34所示，相比峰值强度略低5%，基本与试验相吻合。

图9.25　圆柱体试件单轴压缩应力—应变关系图

图9.26　立方体试件单轴压缩应力—应变关系图

图9.27　立方体再生骨料掺量为0时应力—应变关系

图9.28　立方体再生骨料掺量为40%时应力—应变关系

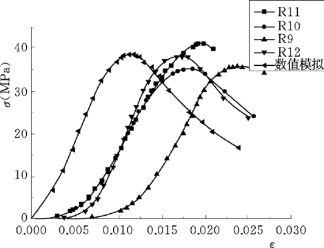
图9.29　立方体再生骨料掺量为70%时应力—应变关系

图9.30　立方体再生骨料掺量为100%时应力—应变关系

图9.31　圆柱体再生骨料掺量为0时应力—应变关系

图9.32　圆柱体再生骨料掺量为40%时应力—应变关系

图9.33　圆柱体再生骨料掺量为70%时应力—应变关系

图9.34　圆柱体再生骨料掺量为100%时应力—应变关系

从图9.25～图9.26中还可以看出，随着再生骨料掺量的增加峰值强度降低，且应力—应变关系曲线上升段斜率也变小即压缩弹性模量变小。将图9.27～图9.34相比较，试验的应力—应变关系图中比较缓慢的上升起始段，主要是因为试验过程中试件和球头之间存在着一定的距离，所以有一定的位移而试件还没有受到压力，而数值模拟则呈线性上升。