优化气藏多口水平井多级压裂实例的Barnett非常规方法

准确布置同一平台钻井的多水平井对于非常规气藏的经济开采十分重要。但是，还存在着高成本、储层渗透率、孔隙度、裂缝间距、裂缝半长、裂缝导流能力及天然裂缝所造成的不确定性等问题。因此，深入研究这些不确定参数的范围以及它们对生产动态的影响，对于改进压裂设计和完井方法是十分重要的。我们将利用Response Surface Methodology（RSM）来优化水平井的布置并利用数值模拟方法，并结合经济分析实现最大化净现值。另外，还要考虑在不同气体解吸附下分段压裂模拟方法对于Barnett Shale生产的影响，设定了渗透率、孔隙度、裂缝间距、裂缝半长、裂缝导流能力以及邻井间距这六个不确定性参数影响范围，并用来拟合响应值函数NPV，最终确定最优设计方案。

这种方法有助于优化井的布置和压裂设计，从而获得最优泄气区，并且有助于理解邻井间的裂缝干扰。另外，还可以用来确定是否需要调整井的布置，从而在实际施工之前修改压裂方案，并确定特定区域的最优水平井数。

1.页岩气藏模拟

利用局部网格加密来精确模拟页岩到裂缝的流动（适当地植入基质到裂缝的不稳定流）；对水力裂缝进行显示模拟；用一些次网格来描述，随着裂缝距离的增加，网格大小呈对数增加，以精确的模拟基质与裂缝间的较大压降；用双重渗透率网格来描述基质—基质和裂缝—裂缝的流动；假设气藏均质，裂缝间距相同；假设没有水的流动；孔隙度及渗透率具有应力敏感性；模拟中气体仅仅通过压裂缝进入井筒（没有基质—井筒的流动）。

用非达西流来模拟裂缝中由于气体高流速产生的紊流；Forchheimer数中的β由式（8—3）确定：

式中，K单位为mD；β单位为ft-1。图8—87为典型的页岩气分段压裂设计图，其中包含了一些重要的裂缝几何参数：外部裂缝、内部裂缝、裂缝间距以及裂缝半长。

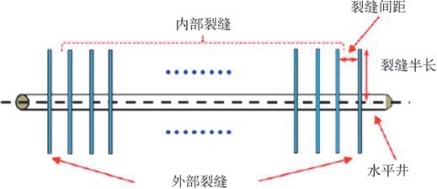
图8—87　典型的页岩气分段压裂设计图

2.经济模型

使用式（8—4）来计算NPV：

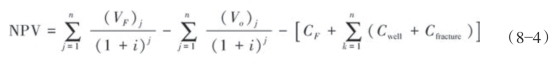
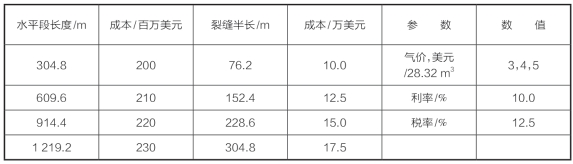
式中，VF为压裂气藏生产收益的未来值；Vo为未压裂气藏生产收益的未来值；CF为总固定成本；Cwell为一口水平井的成本；Cfracture为水平井压裂成本；N为水平井数。经济分析中使用的数据见表8—40。

表8—40　NPV经济分析中的数据

储层在页岩中的气体含量常用朗格缪尔吸附方程（又称朗格缪尔等温式）来描述：

式中，Gs为气体含量，scf/t；VL为朗格缪尔体积，scf/t；pL为朗格缪尔压力，psi；p为压力，psi。

将气体含量单位scf/ft3转换成scf/t时需要页岩地层的密度。朗格缪尔压力pL和体积VL是两个重要的参数。朗格缪尔体积指在无限大压力下气体的体积，它反映了气体的最大储存能力。朗格缪尔压力是指当体积为朗格缪尔体积值的一半时对应的压力。图8—88为Barnett Shale 使用的吸附气量和总气量随压力变化的关系图。图8—89为使用朗格缪尔等温式反映页岩中气体含量的示意图。

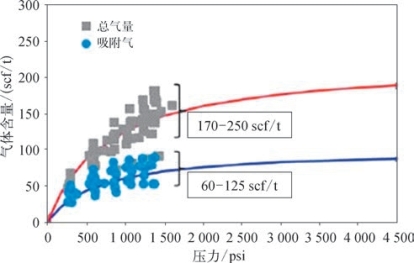
图8—88　Barnett页岩岩心吸附气量和总气量随压力变化的关系图

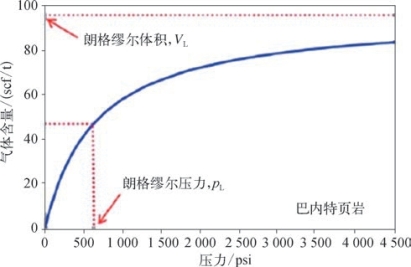
图8—89　利用朗格缪尔等温式反映页岩中气体含量的示意图

3.Barnett页岩历史拟合

历史拟合所使用的气藏信息见表8—41。

图8—90（a）表明当考虑解吸附效应时，数值模拟结果与实际生产数据拟合更好。当生产时间为4.5年时，解吸附对气体产量的贡献为15.6%。

表8—41　历史拟合所使用的气藏信息

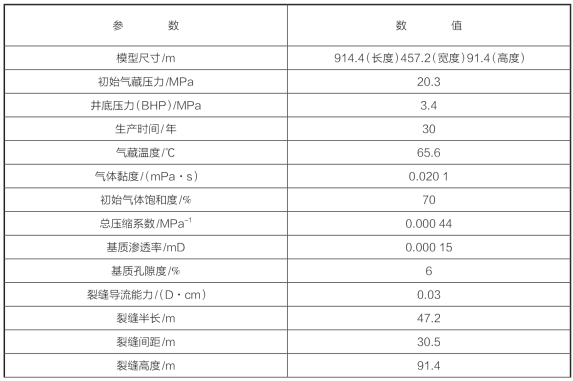
（续表）

图8—90（b）为考虑气体解吸附和不考虑解吸附情况下，对生产30年后产量的预测。从图8—90（b）可知，生产30年后，由于较大的压力衰竭和更大的泄气面积，气体解吸附对气体产量的贡献率为20.7%，故在进行历史拟合和评估Barnett页岩产量预测的时候，气体解吸附的影响是不可忽略的。因此，在后续优化多井布置时还要考虑解吸附影响。

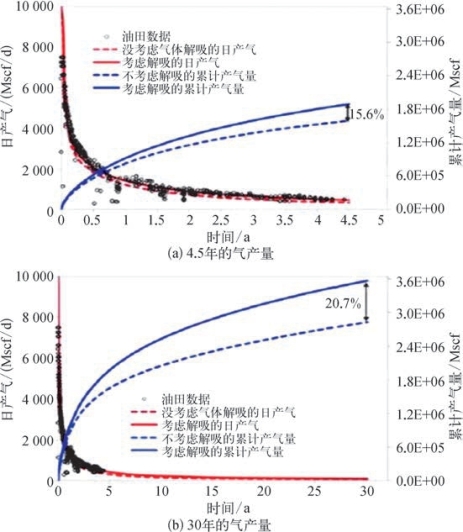
图8—90　考虑气体解吸附和不考虑解吸附效果

4.多井模拟

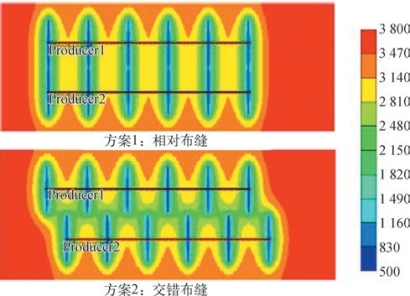
我们研究了两种多井裂缝布置。如图8—91所示，第一种是相对布缝，第二种是交错布缝。我们还研究了裂缝间距对这两种方案产量影响的差别。我们建立了一个页岩气藏模型，有关模拟的气藏信息见表8—42。由图8—92可知，当裂缝间距小于400 ft时，这两种方案的产量几乎没有差别。裂缝间距为400 ft或以上时，方案2的产量比方案1要高。由图8—93可知，当裂缝间距为600 ft时，方案2的平均储层压力降更大，从而累积产量更高。两种方案在生产30年后的压力分布如图8—94所示，由图8—94可知，方案2的有效泄气面积更大。另外，方案2能够增加裂缝之间的应力干扰，产生更大的有效改造体积，从而提高产气量。因此，方案2可用于后续多井布置的优化。

表8—42　气藏模拟参数

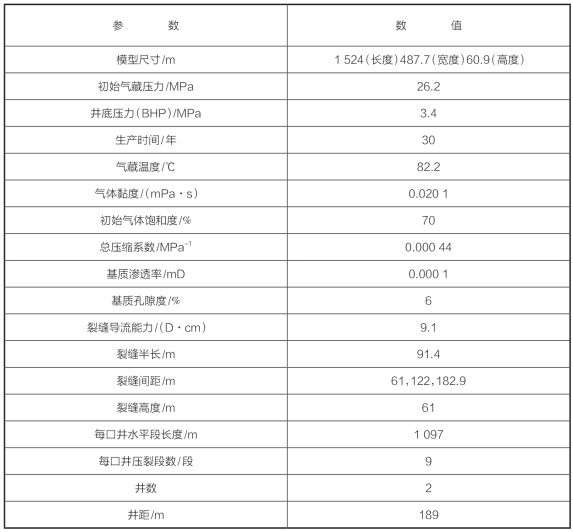
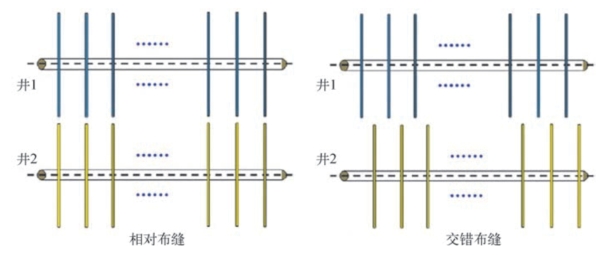
图8—91　两种多水平井布井方案示意图

图8—92　两种布井方案产量对比

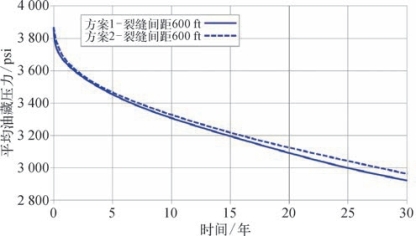
图8—93　两种布井方案平均储层压力对比

(www.xing528.com)

图8—94　两种布井方案生产30年后的压力分布

5.多井优化

基于Barnett Shale 储层资料，利用RSM方法来优化两口水平井的布置。根据最小二乘法，输入变量的变化范围，利用RSM来模拟NPV最大化响应。RSM模型可能是线性或完全二阶的，它能提供一种经济有效和便捷的方式，从而来处理页岩气藏开发中的不确定性。我们建立了一个页岩气藏模型，有关该模型详细的储层参数见表8—43。根据实际最大值和最小值，设定了六个不确定参数的范围（表8—44）。水力压裂缝的数量分别为87和35，相应的裂缝间距分别为40 ft和100 ft。这些不确定参数范围来源于Barnett Shale 储层的现场数据以及模拟数据。基于最优设计，6个变量需要38个方案，根据最优设计方案产生了38个不确定参数组合（表8—45）。不同裂缝间距和裂缝半长条件下，其30年累积产气量和日产气量的对比图如图8—95[（a）（b）]所示。很显然，30年后的累积产气量范围为3 934～6 529 MMscf，而气体产量具有很大不确定性，这说明需要进一步优化。

表8—43　气藏模拟的参数

（续表）

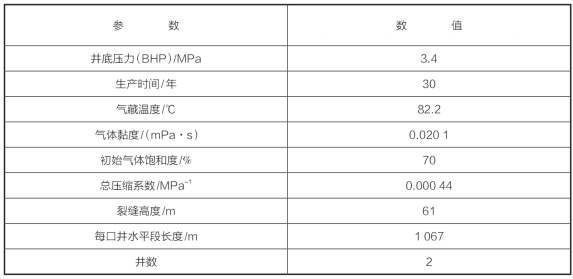
表8—44　不确定参数

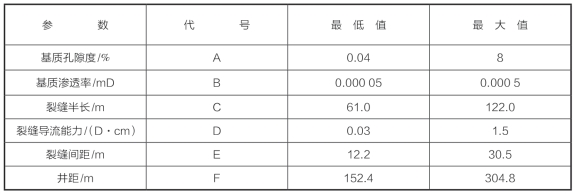
表8—45　最优D设计方案38个不确定参数组合

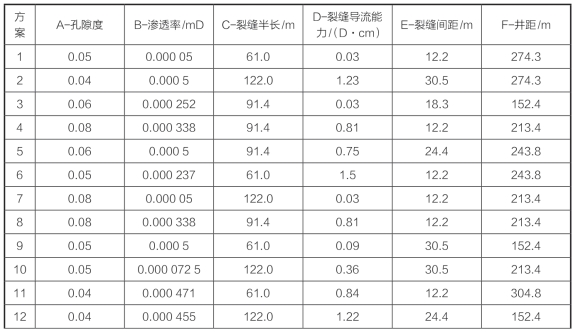
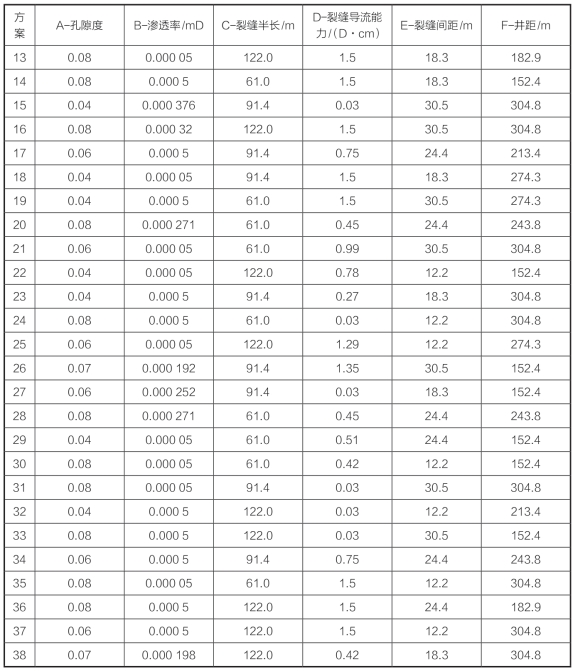
（续表）

一旦获得38个方案的累积产气量之后，便可计算得到相应的NPV值（图8—96）。天然气价对于页岩气藏成功经济开采十分关键，故当计算NPV值和多井压裂优化设计时需考虑气价的影响，从而来确定最优的压裂设计方案。若NPV值为负，表明这是一个非优化方案，不仅会导致没有收入，而且会损失资金。当气价为＄3/Mscf，＄4/Mscf，＄5/Mscf时，对应的NPV范围为＄0.36～13.39 million，＄2.10～18.88 million和＄3.42～24.38 million。

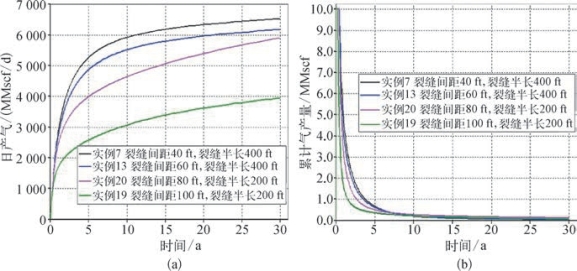
图8—95　不同裂缝间距和裂缝半长条件下30年累积产气量和日产气量示意图

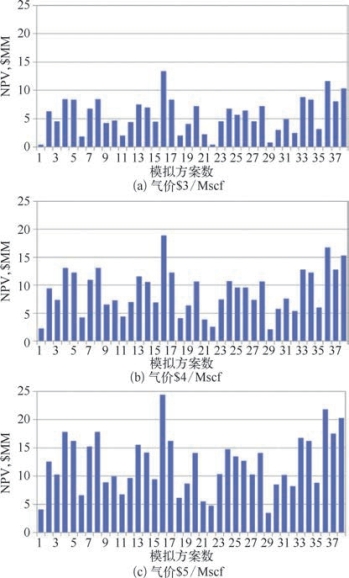
图8—96　38种方案30年期间不同价格时的NPV值

当获得38个方案的NPV之后，利用实验设计软件来建立NPV响应曲面模型。利用统计方法在线性模型、两因子交互影响模型、平方模型、立方模型等模型中选择不同气价下的合适RSM模型。选择模型的标准是最高次多项式模型，并且附加项显著。虽然立方模型是最高次多项式模型，但由于其模型结果离奇所以没有选择。另外，选择合适模型的其他标准还包括具有最大的Adjusted R—Squared以及Predicted R—Squared。因此在后续的压裂优化过程中使用完全平方模型来建立NPV反应曲面。

图8—97为不同气价下的残差正态分布图，图中所有点均落在直线上，这表明残差属于正态分布。

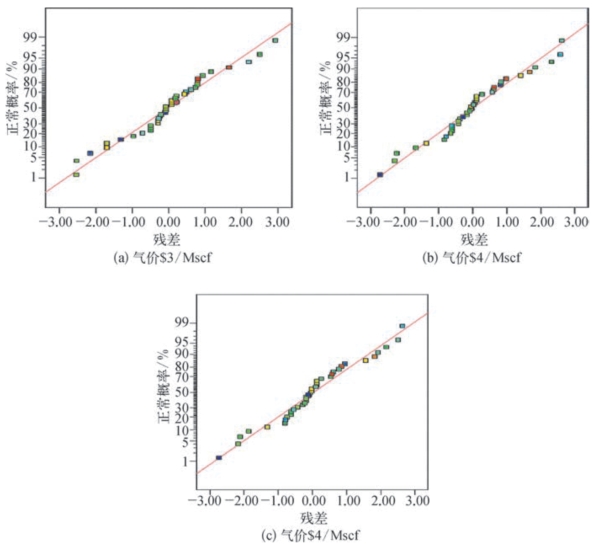
图8—97　不同气价下的残差正态分布图

图8—98为不同气价下预测结果和实际结果对比图，从图8—98可知建立的NPV反映曲面方程是否能够预测实际的NPV值。另外，还可以看出建立的NPV反映曲面模型能否提供可靠的NPV预测值。通过进行对比，表明建立的NPV反映曲面模型是可靠的。

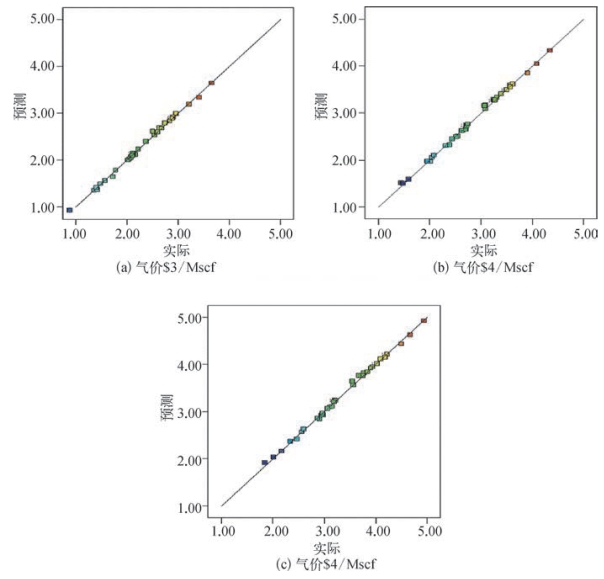
图8—98　不同气价下预测结果和实际结果对比图

图8—99是气价为＄4/Mscf下的井距和裂缝间距的3D曲面，从图8—99可知井距和裂缝间距存在一个最优结合点。当裂缝间距为400 ft时，若井距在研究范围内增加时，NPV值也随之增加。而随着裂缝间距的增加，最优结合点对应的井距也更大。

图8—100反映的是天然气价为＄4/Mscf时井距和裂缝半长的3D曲面，从图8—100可知井距和裂缝半长越大，NPV值也越高。

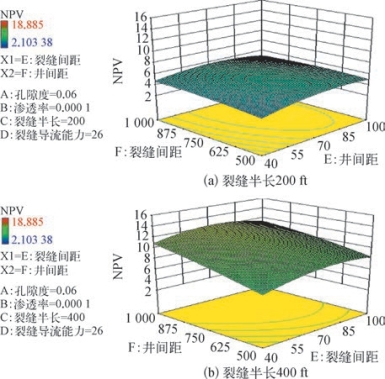
图8—99　气价为＄4/Mscf时半缝长分别为200ft和400ft的NPV3D曲面图

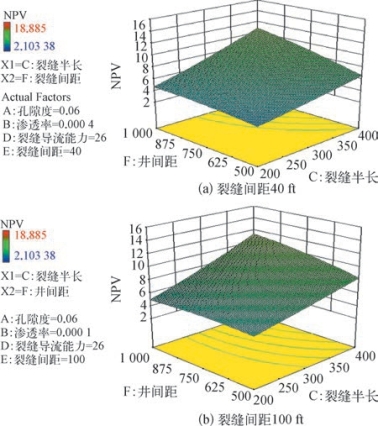
图8—100　气价为＄4/Mscf时半缝长分别为40ft和100ft的NPV3D曲面图

图8—101反映的是气价为＄4/Mscf时裂缝间距和裂缝半长的3D曲面，从图8—101可知也存在着一个最优结合点（裂缝间距值）。随着井距的增加，最优点对应的裂缝半长变大，裂缝间距变小。因此，这有助于压裂和完井设计的优化，从而获得页岩气田的最大经济存活期。

图8—101　气价为＄4/Mscf时半缝长分别为500ft和1000ft的NPV 3D曲面图

表8—46列出了孔隙度为0.06，渗透率为0.000 1 mD时，不同气价下的优化设计结果。如图8—102所示，气价为＄3/Mscf、＄4/Mscf、＄5/Mscf时的最优NPV值分别为8.70 ＄MM、＄12.40 ＄MM和16.34 ＄MM，对应的最优裂缝间距分别为80 ft、70 ft和60 ft。验证最优化方案是极其重要的，可通过在最优化设计条件下运行模拟来进行验证。不同气价下的3种优化方案的累积产气量和日产气量如图8—103所示。NPV的计算值分别为7.91 MM＄、11.81 MM＄和15.75 MM＄。因此，实际NPV值与反映曲面法求得的NPV值差值很小，这表明计算NPV值和真实NPV值之间有较好的吻合。

表8—46　不同裂缝间距及气价下的优化结果

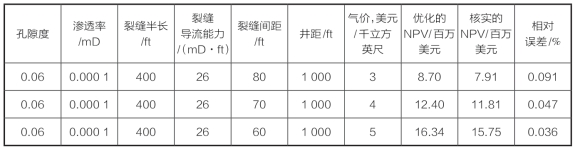
图8—102　不同气价下的最优裂缝间距示意图

图8—103　不同气价下三种优化方案的累积产气量和日产气量示意图

6.小结

页岩气藏是否具备经济开采性取决于压裂段数、裂缝数以及水平井的优化。可应用反应曲面法：即通过优化气藏和2口井裂缝的不确定性参数获得最优设计方案。应用这一方法来优化Barnett页岩开发中6个不确定参数，即渗透率、孔隙度、裂缝间距、裂缝半长、裂缝导流能力以及井距。另外，由于解吸附作用对于Barnett 页岩估算采收率的贡献很大，因此在模拟页岩气藏生产时候需考虑吸附效应。最后，在优化过程中还要考虑气价波动的影响。

当孔隙度为0.06，渗透率为0.000 1 mD，裂缝导流能力为26 mD·ft时，且气价分别为＄3/Mscf、＄4/Mscf和＄5/Mscf时，Barnett页岩最优设计结合点对应的裂缝半长为400 ft，井距为1 000 ft，裂缝间距分别为80 ft、70 ft和60 ft。在Barnett页岩的开发过程中，气体解吸附对其30年累计产气量的贡献率为20.7%。