地层滤失性评价方法

主要研究了由压裂施工资料及强制排液条件下的压降曲线分析地层滤失的方法。

1.压裂施工中对地层滤失性的现场评价

在水力压裂中，地层的滤失性评价是极为重要的，它关系到压裂液的配方调整、压裂施工参数的优化设计和压后配套措施的采取等方面。地层滤失性的评估方法主要有理论计算法、压降分析法、经验公式等。但这些方法本身都有其特有的局限性，因此，本文从压裂施工中的常规资料，如排量、泵注时间等方面，研究了地层滤失性的现场评价方法。它对增加压裂设计的针对性和有效性，确保压裂施工成功和提高压后开发效果等方面都具有一定的现实意义。

假设储层为均匀介质，且裂缝模型为PKN和KGD两种。由质量守恒定律可知，某一时刻T时进入地层的压裂液量，等于此时的裂缝体积和滤失体积之和，其表达式如式（7—32）所示：

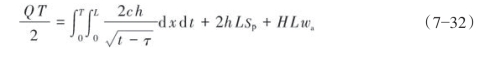
对式（7—32）右端第一项进行拉氏变换，并用卷积定理化简，最终得式（7—33）：

式中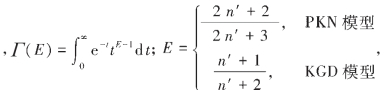它是反映裂缝延伸速率的量，其值域为［0.5，1］；p为拉氏变换像函数中的自变量。

对式（7—33）可用Stehfest数值反演方法获得t时间内的滤失量。

在考虑地层滤失的条件下，PKN模型和KGD模型的造缝半长的计算公式如式（7—34）所示：

平均缝宽的表达式如式（7—35）所示：

上述式中，G为剪模量，其表达式为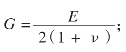：Q为压裂平均排量，m3/min；t为施工总时间，min；L为最终的造缝半长，m；a为停泵时的平均造缝宽度，m；c为综合滤失系数，；h为压裂目的层有效厚度，m；H为裂缝高度，m；Sp为初滤失量，m3/m2；μ为压裂液黏度，mPa·s；G为剪切模量，MPa。

利用上述公式进行计算时，需采用试凑法。即先假设一个滤失系数c，由式（7—34）求出半缝长L，再由式（7—35）求出缝宽wa，最后由式（7—32）求出新的滤失系数c*，如假设值和计算值基本相等，则说明假设的滤失系数c就是真实的滤失系数，否则重新假设c，并重复上述迭代过程，直至结果满足要求为止。

以某气田A井和B井为例，计算结果见表7—6。

表7—6　A井和B井地层滤失计算结果

由表7—6可知，上述模型计算结果与瞬时停泵压力测试结果基本具有一致性。

2.裂缝强制闭合条件下利用压降曲线分析地应力及滤失性

在水力压裂设计及施工中，为了减少压裂液滤液对储层的伤害，同时增加储层中支撑剂的支撑效率（因页岩气井渗透率一般较低，裂缝自然闭合时间较长；另外缝高不易控制，尤其当缝高向下延伸时，如压后靠裂缝自然闭合，会使大多数支撑剂沉降在缝底而影响压后产量），往往采用裂缝强制闭合技术。目前，实施裂缝强制闭合技术的压裂井约占70%以上，而以往的压力降落模型无法对这种压裂井进行有效的解释。因此，本文针对裂缝强制闭合后的压力降落模型进行了推导和求解，并用矿场实例进行了验算，结果基本符合预期的设想。本模型的建立对于加深储层和裂缝参数的认识，对于进一步优化压裂设计和提高全气藏的压裂开发效果，都具有重要的理论意义和现实意义。

1）模型的假设条件

（1）裂缝高度恒定；

（2）压裂排量恒定；

（3）压裂液为幂律流体，且压裂液黏度从井底到缝端呈线性变化或压裂液黏度恒定；

（4）压裂后可以自然闭合，也可强制闭合；

（5）裂缝模型为PKN模型或KGD模型；

（6）压裂停泵后，裂缝仍有延伸，且延伸的规律与停泵前相同；

（7）考虑停泵后延伸裂缝的滤失量；

（8）忽略压裂液的压缩性；

（9）由于停泵后裂缝继续延伸的时间较短，可假设该期间的放喷速度恒定。

2）模型的建立和求解

设压裂泵注时间为tp，停泵后裂缝继续延伸的时间为Δt，刚停泵时的体积为，停泵后Δt时体积为在Δt时间内裂缝体积的变化等于裂缝的滤失量（包括新延伸裂缝的初滤失及滤饼滤失量）与压后Δt时间内放喷量之和，其表达式如下：

将上式左边展开，并忽略二阶无穷小量得式（7—36）：

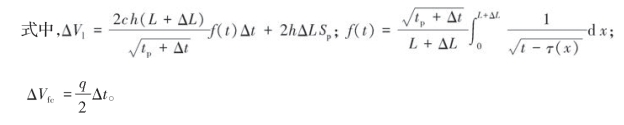
将上述各式代入式（7—36）并移项得式（7—37）：

由裂缝延伸规律（停泵前后相同）得式（7—38）和式（7—39）：

式中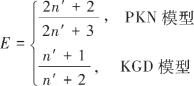，，它是反映裂缝延伸速率的量，其值域为［0.5，1］。

将式（7—38）两端同时除以Δt，并令Δt→0，取极限得式（7—40）：

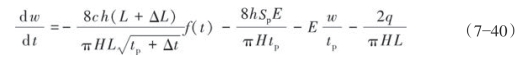
对式（7—40）进行求解得式（7—41）：

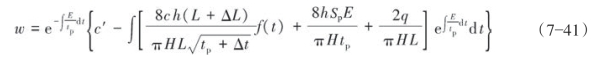
式中，c′为积分常数，由初始条件：t＝tp时

将代入式（7—41）得式（7—42）：

将式（7—42）右端第二项单独提出来积分得式（7—43）：

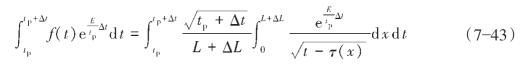
为简便起见，设量纲为1量如下：

再结合式（7—42）得式（7—45）：

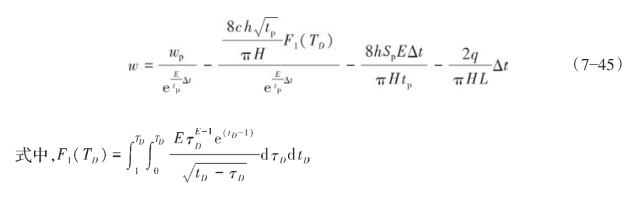
由裂缝的平均宽度公式得式（7—46）和式（7—47）：

式中，

在βs的表达式中，a＝1表示压裂液黏度从井底到缝端呈线性变化，a＝0表示压裂液黏度恒定。(www.xing528.com)

式（7—47）中共有四个未知数，即闭合压力ps，拟合压力p*，停泵时的缝长L和停泵后裂缝的延伸时间Δt，因此，还需再建立三个方程：即根据停泵后裂缝无延伸的压降方程、裂缝的延伸准则方程及施工期间的连续性方程进行辅助求解。

（1）停泵后裂缝无延伸情况下的压降方程

根据上述类似的步骤，得出在区间［tp，tp＋Δt］内任意两个时间点的压力差表达式如式（7—48）所示：

（2）裂缝的延伸方程

根据Perkins理论，裂缝延伸的准则如式（7—49）所示：

（3）施工期间的连续性方程

根据总体积平衡关系，即：总注入体积＝滤失量＋初滤失量＋裂缝体积，得式（7—50）：

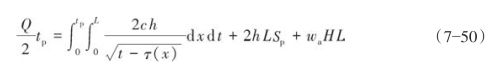
将式（7—50）化简得式（7—51）：

在进行计算时，先假设一个pc，由式（7—47）求出裂缝停止延伸时的压力和对应的时间Δt，然后假设一个L，再由式（7—48）求出拟合压力p*和滤失系数c，然后由式（7—46）求出停泵时的平均缝宽wa，再由式（7—51）求出另一个L*，如计算的L*与假设的L基本相等，则说明假设的L正确，否则需重新假设L，重复上述步骤，并迭代计算至误差满足要求为止。

求出L后，可由式（7—47）求出闭合压力pc，并与先前假设的闭合压力进行对比，如计算值与假设值误差较大，则重新假设闭合压力pc，重复上述步骤，并迭代计算至误差满足要求为止。这样，式（7—47）中的四个未知数均已全部求出。

3）裂缝参数的求解

（1）滤失系数

求出了拟合压力p*后，得式（7—52）和式（7—53）：

（2）停泵时的裂缝宽度

由式（7—46）得平均缝宽的表达式，如式（7—54）所示：

还可得到最大缝宽的表达式，如式（7—55）所示：

（3）停泵时的缝长

不管是PKN模型还是KGD模型，都可按上述步骤得到结果。

（4）停泵后的裂缝延伸长度ΔL

先求出停泵后的裂缝延伸时间Δt，再得裂缝延伸长度ΔL，其表达式如式（7—56）所示：

最终缝长Lf的表达式如式（7—57）所示：

（5）闭合缝宽wc

设支撑剂体积为Vpro，则裂缝闭合的缝宽的表达式如式（7—58）所示：

（6）裂缝闭合时间

由式（7—48）得式（7—59）：

先由式（7—59）求出闭合压力pc，并任选一压力p1和t1，利用试凑法求出闭合时间tc。当然，如测压降时间足够长，可直接由闭合压力值pc确定闭合时间tc（通过压降曲线得出数值）。

（7）压裂液效率

由停泵时的裂缝体积与总注入体积得压裂液效率的表达式，如式（7—60）所示：

上述推导公式中的符号说明如下：tp为压裂泵注时间，min；Δt为停泵后裂缝延伸的时间，min；ΔVl为Δt时间内压裂液的滤失量，m3；ΔVfc为压裂停泵后Δt时间内井口放喷的压裂液量，m3；q为压裂停泵后，单位时间内从井口放喷的压裂液量，m3/min；c为综合滤失系数，；h为储层的滤失高度（有效厚度），m；H为裂缝的高度，m；L为压裂停泵时的造缝半长，m；ΔL为压裂停泵后延伸的缝长，m；为裂缝的宽度，m；p为停泵时的裂缝宽度，m；E为裂缝延伸指数，其值域为［0.5，1］；E′为平面应变模量，MPa；pc为闭合压力，MPa；pisp为瞬时停泵压力，MPa；σT为储层岩石抗张强度，MPa；Sp为压裂液初滤失量，m3/m2；Vpro为压裂加砂量，m3。

某页岩气A井在不同放喷条件下的解释结果见表7—7。

表7—7　A井强制闭合条件下的压降模型解释结果

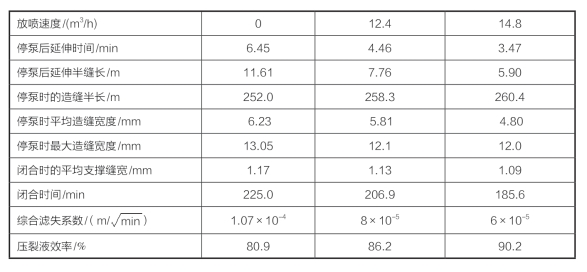
由表7—7可知，压后放喷的油嘴不同，其压降数据的解释结果与自然闭合时的解释结果有很大不同，尤其是综合滤失系数的解释结果差别较大。

3.前置液阶段两次瞬时停泵压力测试法求取滤失的方法

应用前置液阶段两次瞬时停泵压力测试，可判断地层的滤失情况或地应力的变化情况。

一般情况下第二次瞬时停泵压力比第一次要高，原因是压裂液的滤失会使储层流体孔隙压力增加，造成地应力的增加。两次停泵压力差值越大，地层的滤失性也越大。

如裂缝延伸到物性变差且地应力变高的区域，也会造成第二次停泵压力升高。但不管是什么原因造成的第二次停泵压力升高，都应适当增大前置液量或排量。

有时加些细砂或陶粉的措施也是正确的。若是因为滤失大造成的第二次停泵压力增加，肯定需加些细砂或陶粉来降滤；如果是地应力增大造成的，则造缝宽度变窄，容易砂堵。而适当加些陶粉，则可冲刷、打磨窄的裂缝口，使后续加砂更畅通些。现在关于高地应力储层压裂或近井筒摩阻高的储层压裂时，都提倡加细砂或陶粉支撑剂段塞技术。

值得指出的是，第一次停泵时，因地层刚破裂不久，裂缝中充填的可能是井筒中的活性水，而第二次停泵时，则裂缝中充填的大多数是交联的冻胶，故有研究认为两次瞬时停泵压力值没有可对比性，这是一种错误的认识，原因如下：（1）即使第一次停泵时，裂缝中充填的都是活性水，但活性水比冻胶滤失大，因此裂缝壁附近储层孔隙压力增加的多，而地应力也增加较多，所以第一次停泵压力应较高而不是较低；（2）因为停泵时间只有半分钟左右，此时的停泵压力与工作压力的落差，实际上是因为井筒摩阻、孔眼摩阻和裂缝摩阻消失的缘故，是真正的井底裂缝延伸压力。如果停泵测压降时间长（如半小时以上），则压力降低快是正确的，但这里对比的是刚停泵时各种阻力消失后的井底压力；（3）综上所述，由两次停泵压力的差值估算得出的滤失系数实际上被缩小了。

由两次瞬时停泵压力求综合滤失系数的公式如式（7—61）所示：

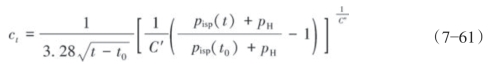
式中，ct为综合滤失系数，；t为任一施工时间，min；pH为井筒静液柱压力，MPa；pisp（t0），pisp（t）为分别为前置液某一时刻t0时的停泵压力，以及压裂施工中任一时刻t时的停泵压力，MPa；C′，C″分别为裂缝几何形状的系数（针对PKN模型，C′＝0.202 33，C″＝0.478 50；而针对KGD模型，则C′＝0.190 3，C″＝0.467 67）。

按式（7—61）计算的滤失系数图如图7—13和图7—14所示。

图7—13　两次停泵压力（井底）计算的滤失系数（KGD模型）

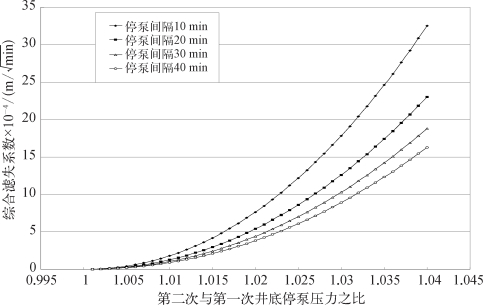
图7—14　两次停泵压力（井底）计算的滤失系数（PKN模型）

如隔层与储层的地应力差值较大或在施工的中后期说明缝高的延伸受到控制，此时宜选PKN模型，否则若预计缝高的延伸较大或在施工的早期则可选KGD模型。