岩石力学参数尤其是就地条件下的岩石力学参数,主要包括泊松比和杨氏模量等,对压裂的优化设计具有重要的影响。它关系到造缝宽度大小、平均砂液比高低、裂缝内的脱砂与否、支撑剂的压碎或嵌入程度大小、支撑剂的类型选择以及其他工艺参数的优选。求取就地条件下的岩石力学参数的主要方法是室内三轴岩心试验和测井资料解释等。实验室三轴测试结果一般较为可靠,但费时、费力,且花费较高,不可能对每口井都进行测试;而测井解释结果一般偏高,有时不太可靠。
因此,需要一种价格低廉、简单易行但结果可靠的方法。尤其是压裂面对的页岩气藏,由于开发成本的制约,不可能花费太多的费用去获取各种资料,包括岩石力学资料。因此,如何利用压裂施工本身所反馈的信息来加深对储层的认识,是摆在广大压裂科研人员面前的一项必须攻关的课题。因此,利用常规的地面压裂施工压力和瞬时停泵压力等资料,初步探讨了求取就地岩石力学参数的新方法,既可用来进行实时分析,也可进行压后评估。
1.由地面压裂施工压力求井底压力的方法
在水力压裂中,正确确定井底施工压力的大小及其变化是分析裂缝延伸状况和评估储层特性的基础。但由于现场的种种原因,在大多数情况下只能获得井口的压裂施工压力。因此,需要一种由井口压力推算井底压力的方法,而这种方法的实质就是要研究混砂浆摩阻与纯携砂液摩阻间的关系。
我们将针对此问题做较为深入的理论研究[3],先求出量纲为1混砂浆摩阻与量纲为1混砂浆密度间的定量关系,然后可根据施工砂液比的大小,计算出混砂浆密度的大小,由此可分段计算出井筒的混砂浆摩阻(井筒纯压裂液摩阻可由相关理论公式计算,或当前置液前期瞬时停泵时井口压力的落差即可近似认为是井筒的纯压裂液摩阻,因为此时孔眼摩阻可忽略;而停泵时地层刚起裂不久,故裂缝的摩阻也可忽略)。结合分段计算的井筒静液柱大小,就可由井口施工压力计算出井底施工压力,从而为分析裂缝的延伸状况及调整施工参数提供了依据。其得出的主要关系式如下式所示:
井口压力与井底压力的关系如式(7—12)所示:
![]()
式中,pbt,pw,pH,pf分别为油管的井底压力、井口压力、静液柱压力和油管摩阻,单位都为MPa。
量纲为1摩阻的定义式如式(7—13)所示:

式中,Δpr为量纲为1摩阻;psf,plf分别为混砂浆和纯携砂液的井筒摩阻,单位都为MPa。
量纲为1密度的定义式如式(7—14)所示:

式中,Δρr为混砂浆量纲为1密度;ρs,ρl分别为混砂浆密度和纯携砂液密度,单位都为kg/m3。
混砂浆密度的计算公式如式(7—15)所示:

式中,SOR为压裂施工砂液比;ρb,ρt分别为支撑剂的体积密度与视密度,单位都为kg/m3。
最后得出量纲为1混砂浆摩阻与量纲为1混砂浆密度间的关系式如式(7—16)所示:
![]()
如现场条件不允许在前置液段停泵,可采用如下的公式近似计算纯压裂液在油管中的摩阻:
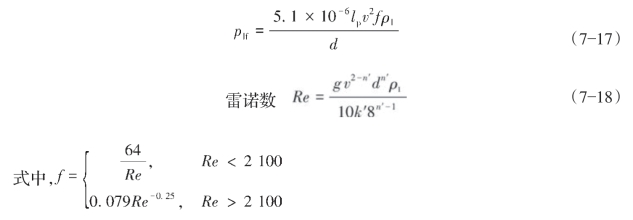
式中,f为量纲为1摩阻系数;v为压裂液在油管中的流动速度,m/s;d为压裂管柱内径,m;n′为压裂液流态指数,量纲为1;k′为压裂液稠度系数,Pa·sn′;g为重力加速度,m·s-2;lp为压裂管柱长度,m。
此外,Hannah及Harrington[4]等认为混砂浆摩阻与纯压裂液摩阻间关系式如式(7—19)所示:

式中,

式中, 为混砂浆中支撑剂的颗粒体积所占的体积分数比。
为混砂浆中支撑剂的颗粒体积所占的体积分数比。
应该指出的是,实际操作时由于井筒中含有不同砂液比的混砂浆段,因此需根据详细的施工泵注程序分段计算,为便于计算可每分钟计算一个点,当然如压力变化较快,则应适当缩短时间间隔,以反映压力的真实变化趋势。
2.就地岩石力学参数与裂缝扩展模型
根据上述计算的井底压力,可初步判断裂缝的扩展形态。一般而言,随着施工时间的增加,Perkins-Kern-Norgren模型(PKN模型)裂缝的井底压力呈现略微增长的特征,而Khristianovic-Geertsma-Dekerk模型(GDK模型)裂缝的井底压力则有一定程度的降低。压裂施工时井底压力的增长模式如图7—12所示。其中,斜率Ⅰ井底净压力上升,表示缝高延伸受到一定限制,这与PKN模型裂缝特征吻合;斜率Ⅳ净压力快速降低,表示裂缝高度出现不稳定增长,这与KGD模型裂缝的特征吻合;斜率Ⅱ净压力基本平稳,表示天然裂缝张开且滤失增大,意味着即将砂堵或者缝高快速延伸;斜率Ⅲ净压力快速上升,表示裂缝内已经出现砂堵。
对页岩气压裂而言,形成的裂缝形态非常复杂,但无论是PKN模型还是GDK模型在裂缝扩展的不同时间内都能体现出相应的压力动态特征。
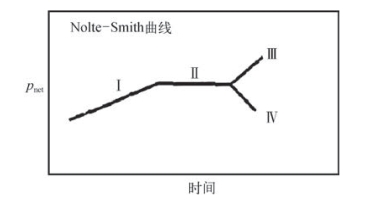
图7—12 压裂施工时井底压力的四种增长模式示意图
1)PKN裂缝扩展模型
考虑滤失与初滤失情况下,任一时刻t时的造缝半长L(t)的表达式如式(7—21)所示:
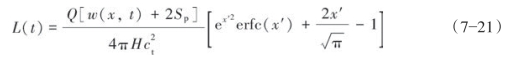
式中,![]() ;erfc(x')为误差余函数。(https://www.xing528.com)
;erfc(x')为误差余函数。(https://www.xing528.com)
任意位置和任意时间的造缝宽度的表达式如式(7—22)所示:
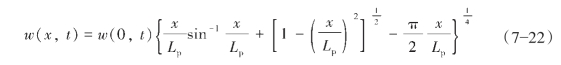
而缝口处缝宽w(0,t)的表达式如式(7—23)所示:

式中,x为沿缝长任一位置距井点的距离,m;Lp为压裂施工结束时的造缝半长,m;Q为压裂泵注排量,m3/min;ct为综合滤失系数,m/min0.5;Sp为压裂液的初滤失,m3/m2;t为任一压裂施工时间,min;ν为泊松比,量纲为1;μ为压裂液冻胶的黏度,Pa·s;H为裂缝高度,m;G为剪模量,Pa。
剪切模量G与杨氏模量E的关系式如式(7—24)所示:

平均缝宽 表达式如式(7—25)所示:
表达式如式(7—25)所示:
![]()
平均宽度表达式如式(7—26)所示:

在βs的表达式中,a=1表示压裂液黏度从井底到缝端呈线性变化,a=0表示压裂液黏度恒定不变。
式中,E为就地条件下的岩石杨氏模量,MPa;E′为平面应变模量,MPa;pc(t)为t时刻缝壁处地层最小的水平主应力(闭合压力),MPa;pbt为任一施工时间的井底施工压力,MPa。
闭合压力pc可通过前置液段开始时瞬时停泵来确定。此时,裂缝刚开始延伸,宽度还较小,可近似认为此时的井底压力(地面瞬时停泵压力与井筒静液柱压力之和)即为地层的闭合压力。闭合压力与泊松比的关系式如式(7—27)所示:
![]()
从而由式(7—27)求出泊松比。
式中,α为Biot弹性系数;σz为上覆地层压力,MPa;ps为目前的孔隙压力,MPa。
值得指出的是,前置液停泵时测得的闭合压力是裂缝刚起裂时的值。实际上随着注入的进行,由于压裂液的不断滤失,沿裂缝壁附近的地层孔隙压力不断增加,会导致闭合压力的增加。滤失系数与不同时间停泵压力的关系式如式(7—28)所示:
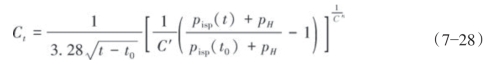
由式(7—28)得式(7—29):
![]()
式中,pc(t0)为前置液某一时刻t0时停泵获得的裂缝闭合压力,MPa;t为任一施工时间,min;pH为井筒静液柱压力,MPa;pisp(t0),pisp(t)分别为前置液某一时刻t0时的停泵压力和压裂施工中任一时刻t时的停泵压力,MPa;C′,C″分别为裂缝几何形状的系数(针对PKN模型,C′=0.202 33,C″=0.478 50;针对KGD模型,C′=0.190 3,C″=0.467 67)。
联合式(7—27)和式(7—29),可求出压裂施工中任一时刻对应的泊松比。
注意式(7—28)成立的前提条件是:储层原始地应力分布比较均匀,且不存在地应力的突变区域。一般情况下,上述前提条件是能成立的。
具体求解杨氏模量时,可先假设一个值,然后在该假设的杨氏模量条件下,要求解裂缝长度L(t)和造缝宽度w(x,t),式(7—21)和式(7—22)需联立求解,并采用试凑法,即先假设一个L(t),由式(7—22)求出一个(x,t),然后再由式(7—21)求出新的L(t),如前后两次L(t)值相差不大,则该值就是真实的缝长,然后由式(7—22)求出真实的造缝宽度(x,t)。否则,循环迭代,直至前后两次L(t)值的误差满足要求为止。求出L(t)和(x,t)后,再由式(7—26)求出相应的井底压力pbt,如pbt和实际的井底压力相同或误差很小,则说明假设的杨氏模量正确,否则需再次假设一个杨氏模量,重复上述步骤,直至误差满足要求为止。
由于每一时间间隔下的井底压力(实际上由井口压力计算出)都对应一个杨氏模量值。按上述步骤可以作出杨氏模量随施工时间变化的曲线。
另外,在上述求解过程中,还需按上述同样的步骤,求出施工结束时的造缝半长Lp。
2)KGD裂缝扩展模型
任一时刻t时的造缝半长L(t)的表达式如式(7—30)所示:

任意位置和任意时间的造缝宽度的表达式如式(7—31)所示:
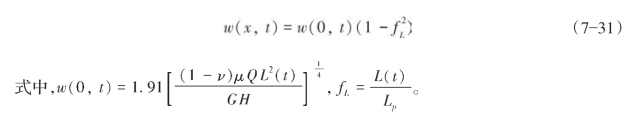
具体求解方法与前面的PKN裂缝模型类似。
按上述方法对两口页岩气井的泊松比和杨氏模量进行了评价,并与岩心实验结果进行了对比,具体结果见表7—5。
表7—5 页岩气两 口井岩石力学评价结果

免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




