新方法优化页岩气水平井分段压裂设计

与常规油气井压裂优化设计相比，由于裂缝的形态复杂，考虑的因素较多［11—14］，故页岩气水平井压裂优化设计要更复杂、更困难。目前，页岩气水平井分段压裂设计是在采用常规砂岩水平井分段压裂设计方法的基础上，应用正交设计原理，对网络裂缝多缝长及多导流能力进行优化［15—16］。实际上，网络裂缝是页岩气水平井压裂设计的最高目标，一般难以实现。多口页岩气水平井压裂后评估结论认为，网络裂缝形成的概率仅为10%左右，单一裂缝为40%左右，其余的则是介于单一裂缝和网络裂缝之间的复杂裂缝［17—18］。可以这样认为，压裂产生的裂缝形态都是复杂裂缝，单一裂缝和网络裂缝都是复杂裂缝的两种特殊表现形式。对于这种特殊的复杂裂缝的表征及压裂优化设计目前还没有一套成熟的方法。为此，下文将提出以裂缝复杂性指数为目标函数的页岩气水平井压裂优化设计新方法。针对水平层理缝发育储层及高角度天然裂缝发育储层，进行了提高裂缝复杂指数方法研究。现场实例表明，该方法可以提高页岩气井产量，并为国内逐渐增多的页岩气水平井分段压裂实践提供理论依据。

1.复杂裂缝的量化表征新方法

目前，虽然已对页岩气水平井分段压裂的裂缝复杂性指数进行了量化表征，但仅给出了不同缝间距及缝长条件下的裂缝复杂性指数的分布范围，并未就复杂裂缝本身进一步细分。例如，同样是复杂裂缝，有的复杂性指数接近单一裂缝的临界值，而有的裂缝复杂性指数却接近网络裂缝的临界值。因此，如果仅粗略讨论复杂裂缝，可能会混淆复杂裂缝本身的差异性，而对裂缝的复杂程度仍然没有清晰的认识，并不能实现压裂设计的最优化。为此，下文将提出一个新的复杂裂缝的量化表征方法。

1）裂缝复杂性指数的新定义

图5—39为水平井分段压裂裂缝示意图。如图5—39所示，假设分支裂缝1～6都相互平行，并都垂直于水力裂缝Ⅱ，且对称分布于水力裂缝Ⅱ的全缝长范围内。根据以往对复杂裂缝指数的定义［9］，将分支裂缝1～6的平均长度与水力裂缝Ⅱ的全缝长的比值，再乘以4因素的叠加因子，所得数值即为裂缝的复杂性指数。该定义认为分支裂缝1～6的流动干扰波及面积正好相互叠置，但实际上分支裂缝的密集程度可能没有达到将上述流动干扰波及面积全覆盖的程度。因此，需提出一种新的裂缝复杂性指数的定义：将不同分支裂缝流动干扰波及面积与水力裂缝Ⅱ的全缝长相除，得到分支裂缝的等效缝宽，该等效缝宽与水力裂缝Ⅱ的全缝长的比值，再乘以4因素的叠加因子。新的裂缝复杂性指数的表达式如式（5—26）所示：

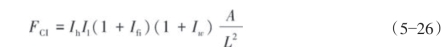
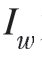式中，A为分支裂缝渗流干扰波及面积，m2；L为水力裂缝全缝长，m；Ih为缝高垂向延伸因子，；Il为缝长延伸因子，；Ifi为缝间应力干扰因子，；为缝宽非平面扩展因子，；h为实际的造缝高度，m；H为贯穿整个页岩厚度的造缝高度，m；l为实际的造缝半长，m；L为预期的主裂缝造缝半长，m；d为水平井相邻裂缝间的诱导应力高于原始水平应力差时的传播距离（从一侧裂缝算起），m；D为水平井相邻裂缝间的段间距的一半，m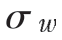；为裂缝半缝宽的均方差，m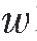；为裂缝半缝宽的均值，m。

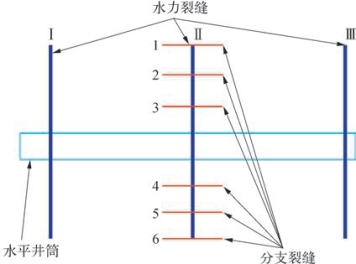
图5—39　水平井分段压裂裂缝示意图

2）分支裂缝流动干扰波及面积的确定

如果完全参照渗流干扰理论，页岩基质的超低渗透性会导致流动影响的区域非常有限。为此，可以将应力干扰区叠加面积近似视为分支裂缝的流动干扰波及面积。在计算应力干扰区叠加面积时，先计算水力裂缝Ⅱ的诱导应力传播区域，再分别计算分支裂缝1～6的诱导应力传播区域，2个传播区域的叠加面积，即为应力干扰区叠加面积。如果水力裂缝Ⅱ的传播距离超过分支裂缝1～6的半缝长，可以用原始水平应力差为界来压缩水力裂缝Ⅱ的诱导应力传播距离。此外，如果分支裂缝净压力太小，其诱导应力传播距离实在有限，可以不考虑取水平应力差为界，而直接取水力裂缝Ⅱ与分支裂缝1～6的流动干扰面积（此时的水平应力差不是原始的水平应力差，而是在考虑水力裂缝Ⅱ已经产生诱导应力的基础上，已经变小了的水平应力差）。

3）分支裂缝的分布及延伸长度的确定

借助前期裂缝扩展物模实验结果［20］，在水力裂缝Ⅱ扩展的过程中，遇到天然裂缝的表现是压力曲线呈现锯齿状波动。出现压力波动的时机反映出分支裂缝距离水平井筒的远近，压力波动的幅度及波幅的宽度反映了分支裂缝的长度及宽度的特征。利用压裂施工综合曲线，可以近似计算出每个分支裂缝延伸的用液量（约等于压力波动波幅的宽度对应的时间与注入排量的乘积）。至于分支裂缝的排量分配，还没有可靠的分配办法，可以假设为注入排量的1/10～1/5，并假设分支缝的端部净压力低于临界应力强度因子后，分支裂缝不再继续延伸。水力裂缝Ⅱ遇到第2个分支缝后，按照同样的方法可以计算出第2个分支缝的长度及宽度。两个相邻分支缝的距离，可以依据压裂施工参数，通过成熟的商业软件如MEYER等模拟计算方法得出。最终，可计算出各分支缝沿水力裂缝Ⅱ全缝长方向的分布，以及每个分支缝的长度及宽度。

将分支裂缝的流动干扰波及面积，以及其长度和宽度，包括其他已知参数，代入式（5—26），即可计算出裂缝复杂性指数。

2.压裂优化设计新方法

为方便计算，可先设定不同分支裂缝在等效缝宽条件下的复杂性指数，计算压裂后形成不同形态裂缝的产量动态及递减规律，从单一裂缝一直计算到网络裂缝。理论上讲，复杂性指数越高，压裂后产量越高，一般很难找到裂缝复杂性指数的拐点值，如图5—40所示。在模拟计算中，常采用ECLIPSE软件，并用具备模拟吸附气的功能模块进行模拟。按前面的图5—39所示方式设置不同复杂性指数的水力裂缝与分支缝分布，通过模拟便可得出不同裂缝复杂性指数条件下的压后产量动态。换言之，压裂优化设计的目标就是在已有施工条件的前提下，最大限度地提高裂缝的复杂性指数。

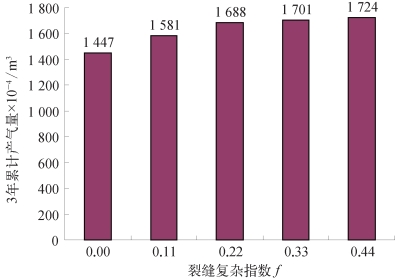
图5—40　不同裂缝复杂性指数下的页岩气水平井压后3年累计产气量的模拟计算结果图

1）水平层理缝或纹理缝地层

在压裂水平层理缝或纹理缝地层时，水力裂缝肯定能沟通层理缝或纹理缝，但不能沟通全部的层理缝/纹理缝，这与天然裂缝情况不同，因为两者的方向刚好相差90°。一般情况下，层理缝或纹理缝的存在是页岩的重要特征，且呈多层叠置分布，它对水力裂缝缝高的增长具有较强的抑制作用，且不能应用常规砂岩或碳酸盐岩的垂向应力差遮挡的概念。

目前，室内实验已证实，当水力裂缝遇到水平层理缝或纹理缝时，实验初期会很快沟通水平层理缝或纹理缝并使之延伸。但由于受实验排量的限制，还未发现水力裂缝接着穿越第2条层理缝或纹理缝的情况。根据能量守恒原则，当水力裂缝穿越第1条层理缝或纹理缝后，由于消耗掉很大一部分能量，已再无能量穿越另外的层理缝或纹理缝。换言之，虽不断注入后续压裂液，但层理缝或纹理缝一旦被沟通，由于其处于地质力学上的弱面，注入能量的大部分会被已延伸的层理缝或纹理缝吸收并继续延伸。实际上，最理想的情况是不同的层理缝或纹理缝都能被依次打开并且都能最大限度地获得延伸，最终形成体积裂缝。为此，可先设计低黏度的滑溜水打开第1条层理缝或纹理缝，等延伸到预期的缝长后，再用高黏度的胶液（线性胶或交联冻胶），另外应尽最大可能提高注入排量，提高打开第2条层理缝或纹理缝的概率，然后再注入低黏度的滑溜水，由于黏度差发生的黏滞指进效应，滑溜水会很快穿过高黏度胶液，在新打开的层理缝或纹理缝里继续延伸。依次类推，最终实现所有层理缝或纹理缝都被打开并被充分延伸的目的。

滑溜水与胶液的注入比例、具体注入体积、排量等参数的设计，要采取循序渐进的原则设计。换言之，胶液的体积及排量设计宜小不宜大，避免一次就打开所有层理缝或纹理缝的情况发生。但也不能太小，太小可能就难以压开第2条层理缝或纹理缝。

从理论上分析，先用高黏度胶液一次将所有的层理缝或纹理缝全部压开，然后改用低黏度的滑溜水同时延伸所有已压开的层理缝或纹理缝，但该设计思路实现的难度较大，因为如果多个水平的层理缝或纹理缝同时延伸的话，其延伸阻力会非常高,而在垂直方向上还有两翼主裂缝会与它们争夺注入的压裂液，显然两翼主裂缝更易吸收大量的压裂液，这主要是由于其流动阻力相对要更小。

因施工现场面临操作上的一些难题，目前在压裂水平层理缝或纹理缝发育程度较好的地层时，一般只应用高黏度胶液，争取先把它们全部压开。随着理论和现场实践经验的丰富和完善，以及技术水平的不断提高，应该能逐步实现上述预期的理想化目标。

2）高角度天然裂缝地层

在遇到高角度天然裂缝地层时，首先要判断该天然裂缝是潜在型（或充填型）还是张开型。

对于张开型高角度天然裂缝，为了降低压裂液滤失量，应当尝试陶粉与常规大粒径支撑剂混合的施工方法，即在遇到张开型天然裂缝后，将陶粉按一定比例和大粒径支撑剂混合后一起注入裂缝中，由于小粒径陶粉的流动阻力小，会优先进入裂缝，而大粒径支撑剂因流动阻力大很难进入天然裂缝，而且天然裂缝的张开宽度可能也不足以使其进入。陶粉用量与天然裂缝发育程度密切相关，最理想的结果是所有的陶粉都进入天然裂缝中，所有的大粒径支撑剂都留在人工主裂缝中，但由于天然裂缝的分布情况很难被准确预测，因而陶粉用量的设计不可能达到最优的。但开始压裂时可先采用小比例陶粉，在压裂施工过程中不断优化，逐步摸索出最佳的混合比例。以前技术人员认为遇到天然裂缝就须快速封堵，不让其延伸，但随着对裂缝复杂性指数认识的不断深入，人们开始认为有必要先延伸天然裂缝，然后再实施封堵。因此，可以采取延缓陶粉的注入时机或降低陶粉的浓度等办法来达到该目的。

对潜在型或充填型天然裂缝，可先计算其临界张开压力。如果临界张开压力很大，而主裂缝净压力又相对较小，则天然裂缝在整个压裂施工过程中是不能张开的。反之，如果临界张开压力很小，在压裂施工过程中天然裂缝会过早张开，使主裂缝的缝长难以达到设计的预期要求。因此，在这种情况下，压裂初期就要优选施工参数（液量、排量、黏度、砂浓度等），从而有效控制主裂缝净压力低于天然裂缝的临界张开压力，等到主裂缝的缝长达到设计要求后，再优选施工参数以提高主裂缝净压力使天然裂缝张开，最终形成沟通近井、远井微裂缝系统的网络裂缝，最终达到充分提高改造体积的目的。

3）天然裂缝分布密度及延伸缝长的定量描述方法

天然裂缝分布密度相对容易计算，可将现场压裂施工的井口压力曲线转变为井底压力曲线，再根据压力曲线的波动情况，结合相关裂缝模拟软件，可识别在主裂缝缝长方向上的天然裂缝分布密度。

主裂缝穿过天然裂缝有以下三种情况：

一是主裂缝遇到张开型天然裂缝。当主裂缝遇到第1条天然裂缝时，压裂液会发生分流，但大部分压裂液仍在主裂缝内。由于天然裂缝缝宽小，压裂液流动阻力大，短时间内裂缝就会停止延伸。当主裂缝遇到第2条天然裂缝时，又发生上述同样的现象，依此类推。(www.xing528.com)

二是主裂缝遇到潜在型或充填型天然裂缝，而未能有效控制净压力。在这种情况下，天然裂缝会过早张开，这与第一种情况比较类似。

三是主裂缝遇到潜在型或充填型天然裂缝，但能有效控制净压力。在这种情况下，直到主裂缝的缝长达到预期要求时，才让所有的天然裂缝张开。由于多个天然裂缝同步张开，相互间竞争压裂液，因而与前两种情况相比，天然裂缝延伸范围会较大幅度缩小，这与限流压裂的分流情况比较类似。

描述每条天然裂缝的缝长及缝宽的一个重点就是确定流量在各裂缝的动态分配，多条裂缝同时存在和延伸时满足Kirchoff第一定律和第二定律，即物质平衡和压力连续准则。对主裂缝穿过天然裂缝的三种情况建立数学模型，可计算不同液量及排量条件下每条天然裂缝的缝长及缝宽，即可定量确定裂缝复杂性指数。

（1）第一和第二种情况下的裂缝扩展模型

这两种情况下，随着压裂施工的进行，天然裂缝的张开数量逐渐增加，即参与分流的裂缝数量不断增加。假设在j-1时刻，主裂缝延伸至第k＋1条天然裂缝且天然裂缝开始张开，则第k＋1条天然裂缝的缝口压力为缝口闭合压力σck＋1，裂缝扩展模型如下式所示：

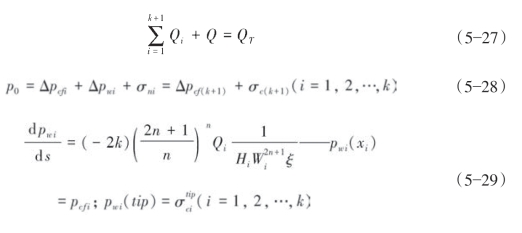
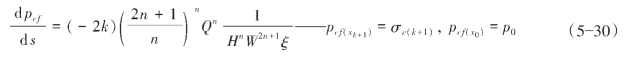
在随后时间里，仍然只有k＋1条天然裂缝，则裂缝扩展模型如下式所示：

（2）第三种情况下的裂缝扩展模型

该情况下假设各天然裂缝同时开启和进液，则裂缝扩展模型如下式所示：

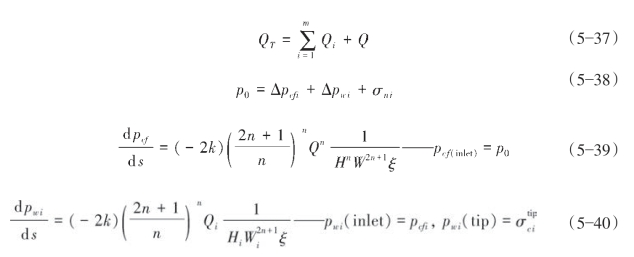
各个天然裂缝的缝宽与缝长的计算公式与式（5—35）～式（5—36）相同。式中，QT为压裂液总排量，m3/min；Q和Qi分别为主缝和主缝中对应第i条天然裂缝的压裂液流量，m3/min；pcf及pcfi为主缝中的压力和主缝中对应第i条天然裂缝位置处的压力，MPa；pi（xi）为主缝中对应第i条裂缝xi位置处的压力，MPa；Δpcfi为主缝中从缝口到第i条天然裂缝的缝中沿程压降，MPa；pi为第i条天然裂缝中的压力，MPa；pi（tip）为第i条天然裂缝尖端压力，MPa；pi（inlet）为第i条天然裂缝缝口压力，MPa；Δpi为第i条天然裂缝中的压力降，MPa；σci及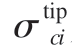为第i条裂缝闭合应力和尖端闭合应力，MPa；p0为主缝缝口压力，MPa；x0及xi分别为主缝缝口位置和主缝中相对于第i条天然裂缝的位置，m。

4）提高裂缝复杂性指数的技术措施

由式（5—27）～式（5—40）可知，要提高裂缝的复杂性指数，关键是尽可能增大天然裂缝的缝长和缝宽，并尽量使主力缝的转向次数增多。在纵向上，尽可能多地压开所有的层理缝或纹理缝，并让其最大限度地获得延伸。从而可在纵向和横向方向上最大限度地提高三维裂缝的改造体积，实现压裂效果的最大化。

（1）延伸天然裂缝的主要技术措施。一是要降低压裂液的黏度，使其尽可能多地进入天然裂缝，促使天然裂缝不断延伸，并可通过模型计算延伸的缝长及缝宽；二是控制陶粉的加砂时机、浓度和段塞量等参数，但目前还无法实现定量模拟。

（2）促使主裂缝多次转向的主要技术措施。由于主裂缝内存在压力梯度，压力梯度越小，主裂缝转向的概率越大。可采用低黏度压裂液和降低排量等措施来降低缝内的压力梯度；其次，要最大限度地提高主裂缝的净压力，除了可以优化压裂液黏度、液量、排量及施工砂液比等参数外，还可以采用人工转向技术，如应用缝内暂堵剂等。

3.应用实例

某区块A井和B井两口页岩气井位于同一平台，其水平段长度、压裂段数及施工压力都比较接近，具体参数见表5—15，压裂施工曲线如图5—41所示。其中，B井采用上文所提出的新方法进行了压裂设计，A井则未采用上述新方法进行压裂设计。

表5—15　某区块两口页岩气井施工参数及无阻流量对比

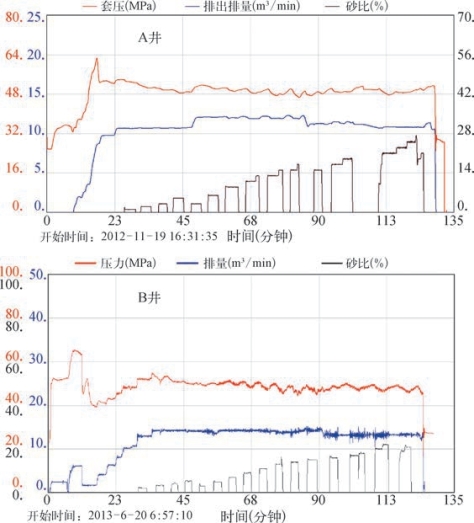
图5—41　A井和B井压裂施工曲线

根据笔者提出的压裂优化新方法，增大液量和排量是提高裂缝复杂性指数的有效措施，因此，B井的单段施工液量比A井约高214 m3，排量高2～3 m3/min。根据式（5—26）计算得到A井的裂缝复杂性指数为0.13，B井的裂缝复杂性指数为0.16，两口井压后无阻流量分别为16.74×104和21.18×104 m3/d。因此，当采用新方法对压裂施工参数（排量和液量等）进行优化后，气井的裂缝复杂性指数及压后产量都得到了明显提高。

表5—16　某区块两口页岩气井裂缝复杂性指数

4.小结

（1）在已有页岩气水平井裂缝复杂性指数的基础上，充分考虑了各分支裂缝沿主水力裂缝方向的分布密度及其相互间流动干扰波及面积，提出了新的裂缝复杂性指数的表达式，使其不仅仅是一个范围，而是一个具体数值。

（2）初步建立了以最大限度地提高裂缝复杂性指数为目标函数的页岩气水平井分段压裂优化设计新方法，针对层理缝或纹理缝，以及不同性质的天然裂缝特征，建立了针对性的设计方法，并从量化的角度进行模拟分析，以增强现场可操作性。

（3）矿场应用实例表明，上述新的设计方法能较大幅度提高裂缝的复杂性指数和压裂后的产量，对提高页岩气开发效果及水平具有重要的现实意义。

（4）建议对水力裂缝与层理缝或纹理缝及天然裂缝的相互干扰，以及扩展互动情况进行三维的模拟分析，并与相应的物理模拟相结合，最终完善优化页岩气水平井裂缝复杂性指数优化设计方法。