裂缝导流能力优化技术探讨

Peter Valko和Economides在水力压裂中引进物理优化技术，将水力压裂井生产指数最大化，即UFD方法。引入了支撑剂数概念Nprop［1］，如式（5—18）所示：

式中，Ix为穿透比；CfD为量纲为1的裂缝导流能力；Vres为产层泄油体积；Vp为支撑裂缝体积（注入体积乘以支撑裂缝与动态裂缝高度比）；kf为支撑裂缝渗透率；k为产层渗透率；xe为井的泄油半径。

对于给定的Nprop值，存在一个最佳的量纲为1的裂缝导流能力使得生产指数最大化。

当Nprop值较低时，裂缝最佳量纲为1的导流能力CfD＝1.6，最大的量纲为1的生产指数JD＝1.909。当支撑体积增加或产层渗透率降低时，最佳量纲为1的裂缝导流能力略有增加。

实现最大量纲为1生产指数与支撑剂数的函数关系式如式（5—19）所示：

支撑剂数与最佳量纲为1的裂缝导流能力的函数关系式如式（5—20）所示：

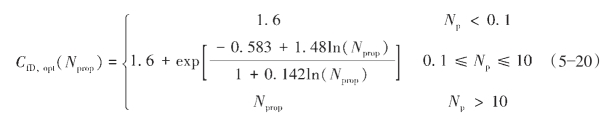
当最佳量纲为1的裂缝导流能力确定后，最优裂缝长度和宽度如式（5—21）和式（5—22）所示：

不同支撑剂数条件下的压后产气指数与量纲为1的裂缝导流能力的关系如图5—30和图5—31所示。其中，支撑剂数较低情况如图5—30所示，支撑剂数较高情况如图5—31所示。一般而言，页岩气由于超低的基质渗透率，支撑剂数会相对较高，此时采用图5—31反映的情况来优化页岩气的量纲为1导流能力较为理想。(www.xing528.com)

图5—30　量纲为1裂缝导流能力与生产指数关系（Nprop≤0.1）

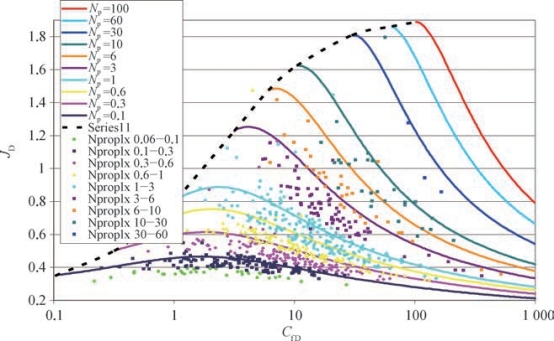
图5—31　量纲为1裂缝导流能力与生产指数关系（Nprop＞0.1）

由图5—31还可知，对页岩气压裂而言，渗透率越低对应的量纲为1裂缝导流能力也越高。

不同页岩气藏长宽比条件下，其量纲为1导流能力、压后采气指数及优化缝长与支撑剂数的关系如图5—32所示。不同支撑剂数条件下，其压后采气指数与页岩气藏宽长比的关系如图5—33所示。

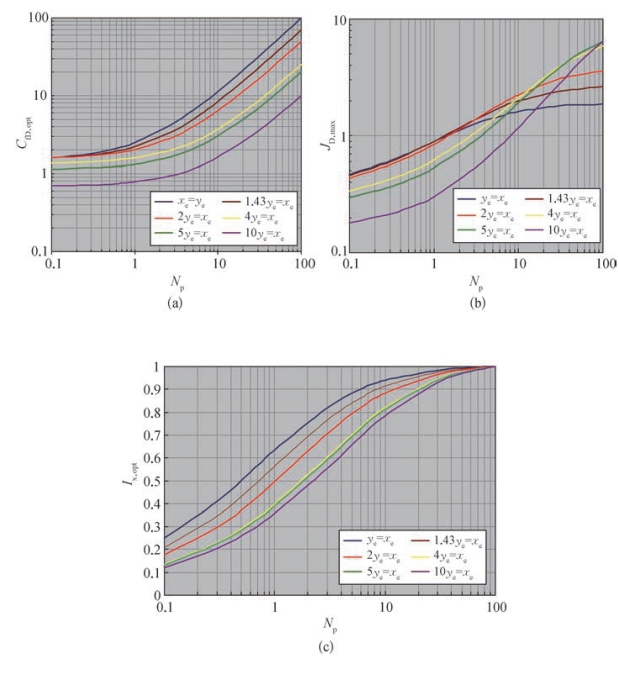
图5—32　不同页岩气藏长宽的条件下支撑剂数与量纲为1裂缝导流能力、最大生产指数和穿透比优化设计

图5—33　不同支撑剂数条件下水力裂缝纵横比与最大生产指数优化设计

由上述两图可对裂缝的导流能力进行优化。