基于页岩破裂压力的新方法，表征脆性指数

大量的压裂实践证明，页岩破裂压力特性与页岩的脆性指数密切相关［53—54］。如脆性指数好，在升排量压裂过程中，即使很小的排量也会出现破裂现象，直至设计排量时还会出现多次破裂现象。反之，如页岩的塑性特征强，则直至设计排量前也难以出现明显的破裂特征。

本书着重从能量的角度来反映脆性与塑性的特征。对强塑性页岩而言，地层破裂后压力几乎不变，但变形一直持续存在，此时消耗的能量是最大的，该能量即可简化为变形长度与变形期间几乎恒定的压力的乘积。该乘积反映到水力压裂施工参数上，可等效为施工压力（井口压力必须转换为井底压力）、施工排量及施工时间的乘积。考虑到在此变形期间，压力、排量等可能一直是变化的，必须采用在施工破裂期间内井底施工压力与排量的乘积，并对时间进行积分来求得。为简化起见，可假设地层破裂变形期间的排量是恒定的。

同样地，对脆性强的页层而言，当地层破裂后压力快速下降，显然此时消耗的能量就相对较小。

按上述脆性地层与塑性地层消耗能量不同的思路，则对于完全的塑性页岩，地层破裂后压力一直处于峰值且恒定不变，形变匀速增加，此时消耗的能量最大，并将其作为基数，其脆性指数为0；而对于完全的脆性页岩，地层破裂后压力应呈直线式下降，即压力几乎快速降低到最小值，其脆性指数为1。

上述定义的完全的塑性页岩及完全的脆性页岩是两个临界极值点，大部分情况下的脆性指数介于两者之间，此时脆性指数的表达式见式（2—12）：

式中，BI为页岩的脆性指数，量纲为1；Ep为完全的塑性页岩破裂后消耗的能量，J；Eb为完全的脆性页岩破裂后消耗的能量，J。

就水力压裂施工而言，上述能量可转变为井底施工压力与排量的乘积，并对时间进行积分，表达式见式（2—13）：

按上述假设，破裂变形期间的排量保持恒定，则式（2—13）中与排量有关的井筒摩阻pf也是恒量，则式（2—13）可转变为：

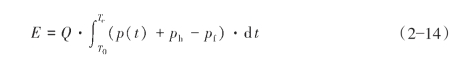(www.xing528.com)

式中，E为压裂消耗的能量，J；Q为压裂施工排量，m3/min；p（t）为井口施工压力，MPa；ph为静液柱压力，MPa；pf为井筒摩阻压力，MPa；Tc为地层破裂变形后压力下降到最低值时的时间，min；T0为地层变形后压力上升到最高值时的时间，min。

将式（2—14）代入式（2—12）并考虑到塑性与脆性的不同特性得：

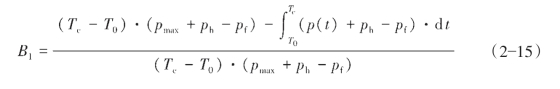
式中，pmax为页岩塑性形变过程中井口压力上升到的最高值，MPa。

为更加直观还可用图形表示脆性指数覆盖的能量区域面积示意图，如图2—19所示。

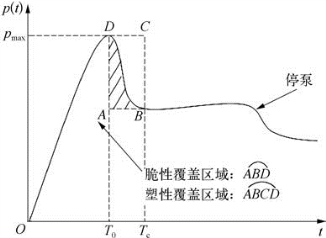
图2—19　压裂施工曲线中的塑性与脆性覆盖的能量区域面积示意图

对于出现多次破裂的情况而言，每次破裂情况都可按上述同样的方法进行处理，但不同之处是不能将每次得出的脆性指数进行简单的算术平均，因每次压裂施工排量不同，脆性指数覆盖的能量区域的比例也不同，理想的处理方法是将每次脆性指数覆盖的能量区域面积求和，再与塑性指数覆盖的能量区域面积之和相除，最终得出的脆性指数就综合反映了施工排量的权重因素。同样，为更加直观，可用多次破裂的脆性指数求取方法示意图，如图2—20所示。

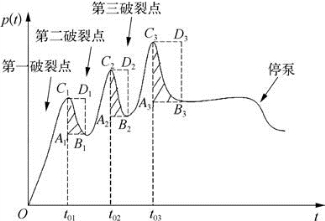
图2—20　压裂施工曲线中多次破裂时的塑性与脆性覆盖的能量区域面积示意图

按上述方法求取的页岩脆性指数，综合考虑了以往方法考虑的页岩硬度、强度及岩石力学特性等参数，由于这些参数的综合作用，故在宏观上反映的就是压裂中岩石变形及破裂特征。同样，上述示例的页岩按此方法计算的脆性指数为54.8%，与用表2—4中20个公式计算出的结果都不同，但由于此结果考虑了各因素在力学宏观上的综合作用效果，故其结果应更为可靠。