威布尔分布单元的可靠性评估方法

随着可靠性评估工作的深入，威布尔分布型产品可靠性评估越来越引起人们的关注。由于威布尔含分布有两个或三个参数，因此比指数分布适应能力强，在各个领域中有许多现象近似地符合威布尔分布。

1.两参数威布尔分布

两参数威布尔分布的分布函数为

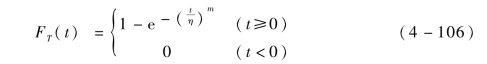
式中：m——威布尔分布的形状参数，m ＞0；

η——威布尔分布的尺度参数，η ＞0。

如果令x=lnt，则x 服从极值分布，分布函数为

式中：。

这样，极值分布的成果就可以应用到威布尔分布上来。

1）非替换（右侧）定数截尾寿命试验的情况

在一批产品中随机抽取n 个产品进行寿命试验。试验到有r 个样品失效时截止，r 个样品的失效时间按从小到大的次序排列为

t（1）≤t（2）≤…≤t（r）

于是有

lnt（1）≤lnt（2）≤…≤lnt（r）

即

X（1）≤X（2）≤…≤X（r）

（1）点估计。

极值分布参数μ 和σ 的最好线性不变估计为

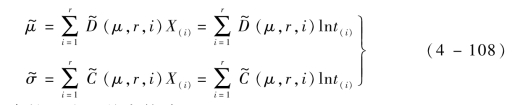
威布尔分布参数m 和η 的点估计为

可靠寿命tR 的点估计为

式中：R——可靠度预定值。

可靠度R 的点估计为

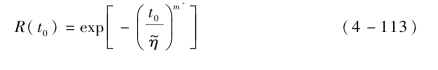
式中：t0——工作时间。

如果该产品间进行歇式工作，每次任务时间为tz，产品累计工作时间为ts，则该产品完成下一次任务的可靠度R 的点估计为

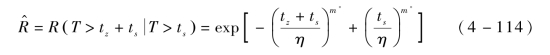
（2）区间估计。

①m 的置信区间估计。

以1-α 为置信度的双侧置信区间为

以1-α 为置信度的单侧置信下限为

②可靠度为R 时可靠寿命t（R）的以1- α 为置信度的双侧置信区间和单侧置信下限如下：

t（R）的以1-α 为置信度的双侧置信区间上、下限分别为

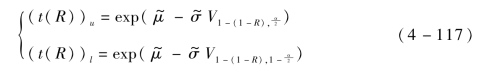
t（R）的以1-α 为置信度的单侧置信下限为

③η 的以1-α 为置信度的双侧置信区间和单侧置信下限如下：

η 的以1-α 为置信度的双侧置信区间上、下限分别为

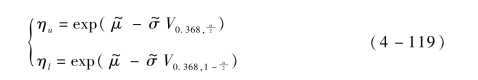
η 的以1-α 为置信度的单侧置信下限为

④可靠度R 的单侧置信下限如下：

对于任意给定的工作时间t0 的可靠度R（t0）的置信下限，可由V1 -p的分位数求得。令x0 =lnt0，计算

当置信度为γ 时，可得与VR（t0）相近的两个V1 -p，γ值，然后用线性插值法求得与VR（t0）相应的Rl（t0）。

⑤任务可靠度R 的单侧置信下限如下：

如果该产品进行间歇式工作，每次任务时间为tz，该产品累计工作时间为ts，应采用式（1-188）计算产品完成下一次任务的以1- α 为置信度的置信下限，即

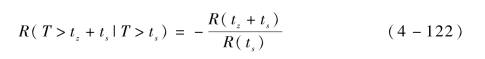(www.xing528.com)

式中：R（tz +ts）——工作时间为tz +ts 的可靠度单侧置信下限，可通过式（4-121）用线性插值法求得；

R（ts）——工作时间为ts 的可靠度单侧置信下限，可通过式（4-121）用线性插值法求得。

以上介绍的两参数威布尔分布非替换（右侧）定数截尾寿命试验的线性不变估计，在子样容量较小时，具有较高的精度。

2）非替换（右侧）定时截尾寿命试验的情况

关于两参数威布尔分布各种估计量的推导都是在基于定数截尾的情况下求得的，对于定数截尾尚没有精确的区间估计方法。为了应用方便，在总试验时间基本相等的条件下，将定时截尾试验转换为定数截尾试验，其试验产品的数目为：

式中：T0——定时截尾所规定的试验时间。

这样，就可以按照定数截尾来处理。

2.三参数威布尔分布

三参数威布尔分布的密度函数为

其分布函数为

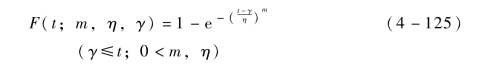
与两参数威布尔分布相比，多了一个位置参数γ。

有许多情况适宜用三参数威布尔分布参数模型来描述产品的寿命分布，但假如把γ 正式当作未知参数处理，问题就困难得多。通常，较好的办法是假设γ已知，于是可把观察值处理成t-γ，然后当作来自两参数威布尔分布的样本处理。因此，三参数威布尔分布参数的问题就变成如何估计位置参数γ 的问题。

在统计推断中，大致有两类分析法：一类是图分析法，另一类是数值分析法。图分析法是使用各种图纸和坐标纸进行分析的方法，容易掌握，既简便易行，又直观易懂。在使用数值分析法估计三参数威布尔分布的位置参数γ 有困难时，可采用图分析法。图分析法也有缺点，即所得到的结果受主观影响较大，精确性也较低，但对于精确性要求不高的威布尔分布位置参数来说不失为一种好方法。当然，在实际的分析中最好将图分析法与数值分析法结合使用。

1）威布尔概率坐标纸

威布尔概率坐标纸是按照威布尔分布原理制作出的，其结构如图4- 14所示。

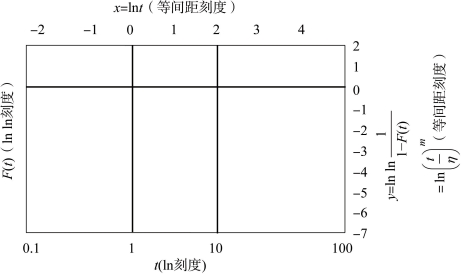
图4-14　威布尔概率坐标纸的结构

考虑式（4-125），令γ =0，有

进行移项，有

取自然对数，有

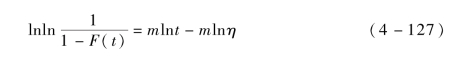
如今

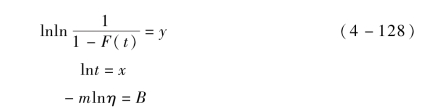
代入式（4-127）可得一直线方程

如果x 和y 的刻度是等距离的，则y=mx+B 便是一条直线。

例如图4-14 中的横坐标，上方x = lnt 是等间距刻度，下方t 是自然对数刻度；纵坐标右侧是等间距刻度，左侧F（t）为lnln 刻度。

由于直线方程式（4-129）是当γ =0 时推导出来的，因此当γ =0 时，各试验点位于一条直线上，这种情况下的尺度参数η 和形状参数m 的估计如下。

2）尺度参数η 的估计

在式（4-129）中，令y =0，则得t = η，应用这一原理，图4-15 中的回归直线AB 与x 轴相交的点E，满足y=0 的条件。因此，由E 点作垂线读出t坐标轴上的刻度值，满足t=η 的条件，即读数就是η。

3）形状参数m 的估计

由式（4-129）可以看出，在横坐标为x=lnt、纵坐标为的坐标系中，m 为由试验数据得到的回归直线的斜率。因此，在图4-16 中将回归直线AB 平行移动至直线A′B′的位置，即使它通过C 点（x =1，y=0），则该直线与纵坐标轴（x=0）相交的D 点的纵坐标值即m 的数值。

4）位置参数γ 的估计

前面已经说明，尺度参数η 和形状参数m 的估计都是在位置参数γ =0 时得到的，但实际情况是，有时γ≠0。这时就需要首先对位置参数γ 进行估计，然后根据估计所得的γ 值进行数据变换，转化为位置参数为零的问题。现以常遇到的γ ＞0 的情况为例进行说明。当γ ＞0 时威布尔分布函数为

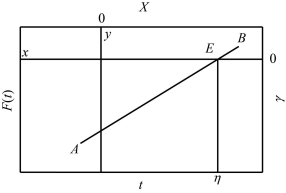
图4-15　η 的估计

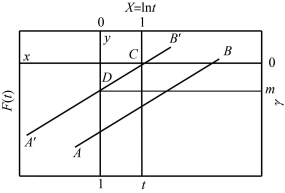
图4-16　m 的估计

进行数据变换，令t′ =t-γ，代入式（4-130），有

这样，在威布尔概率坐标纸上描点，F（t）的图形是一条曲线，F（t′）的图形是一条直线（图4-17）。根据变换，t′ =t-γ 和F（t′）=F（t）。这条直线是把曲线上的各点移动到γ 后得到的。

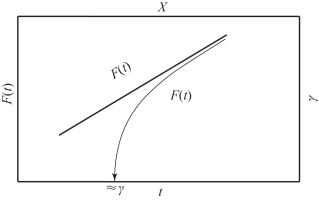
图4-17　γ ＞0 时威布尔分布函数的直线化

由此，可以得到估计γ 的步骤为：

（1）由实际得到的数据，在威布尔概率坐标纸上描点（t，F（t））。根据这些点拟合一条平滑曲线。

（2）沿这条平滑曲线顺势延长到和t 轴相交，交点的刻度就是γ 的估计值γ^。此时F（t）＜0.001，接近零，这样的估计是可以的。如果在F（t）数值较小时，所描的各点比较分散，不能像前面所讲的那样，可以顺势沿曲线延长和t 轴相交。遇到这种情况时，可以先定出一个γ 的均值，在已描的各点中，按F（t）值的大小次序，选3 ～5 点，左移γ，看移动后所得的各点是否大致在一条直线上；如果仍不在一条直线上，修改γ 后再试。

（3）确定γ 的估计值，把所描的各点全都左移γ，将移动后所得的各点作回归直线。

（4）按前述方法对尺度参数η 和形状参数m 进行估计，看其与用图形估计的结果是否一致。如果差别较大，则回到步骤（2）重新调整γ；如果一致，则三参数威布尔分布的问题就转化为两参数的问题了。