指数分布是一种很重要的寿命分布类型,在武器装备的可靠性分析中,有许多装备以指数分布为假定的寿命分布,并以此为根据作统计推断。指数分布可分为单参数指数分布和两参数指数分布两种类型。
1.单参数指数分布
1)点估计
前面已经提到由不同的寿命数据类型将会得到不同的推断方法。下面介绍几种与实际工作比较接近的数据类型。
(1)非替换(右侧)定数截尾寿命试验的情况。
假定:
①t1,…,tn 为相互独立同分布的单参数指数分布;
②以其大小次序排列为t(1)≤t(2)≤…≤t(n);
③试验进行到t(r)时停止,也就是进行到第r 个失效时为止,t(1)≤t(2)≤…≤t(r)(0 <r≤n)。
a.平均寿命θ 的估计量。
式中:
b.失效率λ 的估计量。
c.可靠度R(t0)的估计量。
式中:t0——预先给定的任务时间。
(2)非替换(右侧)定时截尾寿命试验的情况。
假定:
①t1,…,tn 为相互独立同分布的单参数指数分布;
②以其大小次序排列为t(1)≤t(2)≤…≤t(n);
③寿命试验进行到预先规定的时间τ 停止,若在τ 以前有r 个失效,即t(1)≤t(2)≤…≤t(r)≤τ。
a.平均寿命θ 的估计量。
式中:
b.失效率λ 的估计量。
c.可靠度R(t0)的估计量。
式中:t0——预先给定的任务时间。
(3)非替换混合截尾寿命试验的情况。
假定:
①t1,…,tn 为相互独立同分布的单参数指数分布;
②以其大小次序排列为t(1)≤t(2)≤…≤t(n);
③寿命试验进行到预先规定的时间τ 停止,r 为预先规定的停试失效个数,若在τ 时刻已失效的个数为r′,记为
式中:
a.平均寿命θ 的估计量。
b.失效率λ 的估计量。
c.可靠度R(t0)的估计量。
式中:t0——预先给定的任务时间。
(4)非替换定时间隔测试的寿命试验的情况。
假定:
①t1,…,tn 为相互独立同分布的单参数指数分布;
②测试时间为![]() ;
;
③t1,…,tn 满足(τi-1,τi)时间间隔的个数为ri 个(i =1,2,…,l),因此有![]() 个落入
个落入![]() 内。ri(i=1,2,…,l)是随机的,令rl+1 =
内。ri(i=1,2,…,l)是随机的,令rl+1 =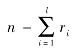 。
。
在上述假定中,如果各测试间隔的中点和长度各为
若是等时间隔的,即h1 =h2 =… =hl =h,则θ 的估计量为
如果只测试一次,即l=1,则θ 的估计量为
当h1,h2,…,hl 并不相等,但max{h1,h2,…,hl} 相对于
很小时,则![]() 为近似估计量。gi(i=1,2,…,l)由式(4-28)给出。
为近似估计量。gi(i=1,2,…,l)由式(4-28)给出。
如果
或
则其近似估计量
如果式(4-30)中max{h1,h2,…,hl} 相对于![]() 很小,可以得到
很小,可以得到![]()
![]() ,这就是式(4-31)。
,这就是式(4-31)。
对于平均寿命很长的产品来说,若测试间隔较短,可以利用式(4-28)作为平均寿命θ 的估计量,进一步也可以用非替换定时截尾子样作近似,式(4-28)也就是式(4-13)的估计。失效率λ、可靠度R(t0)的估计量可分成不同情况依据上述平均寿命θ 的估计量分别给出。
(5)非替换定时逐次截尾寿命试验的情况。
假定:
①n 件随机抽取的试件同属一个母体,即每个试件的寿命服从同一个单参数指数分布;
②在寿命试验中有r(随机的)个失效试验,其失效时间为t(1),t(2),…,t(r);
③在寿命试验中,预先确定k 个时刻τ1 <τ2 <… <τk。在τ1 时刻,在未失效的试件中随机的停试b1 个试件;在τ2 时刻,在未失效的试件中随机停试b2个试件……在τk 时刻,停试bk 个未失效的试件,使得
在上述假设下,平均寿命θ 的极大似然估计量为
式中:
(6)非替换定数逐次截尾寿命试验的情况。
假定:
①n 件随机抽取的试件同属一个母体,即每个试件的寿命服从同一个单参数指数分布;
②在寿命试验中有r 个(预先给定的)失效试验,其失效时间为t(1),t(2),…,t(r);
③在t(1)时,从未失效的试件中随机停试b1 个试件;在t(2)时刻,在未失效的试件中随机停试b2 个试件……在t(r)时刻,将所有未失效的试件都停试,并有
在上述假设下,平均寿命θ 的极大似然估计量为
式中:
若b1 =b2 =br-l =0,则式(4-37)即定数截尾式(4-14)的情况。
2)区间估计
单参数指数分布的区间估计与点估计一样,下面分别对不同的数据类型进行讨论,在给出双侧置信区间的同时,对平均寿命θ 和可靠度R(t0)给出其单侧置信下限(左单侧置信区间),对失效率λ 给出其单侧置信上限(右单侧置信区间)。
(1)非替换(右侧)定数截尾寿命试验的情况。
①平均寿命θ 的估计量。
双侧置信区间(置信度为1-α)为
或
式中:Tr,n——由式(4-14)给出;
![]() 分布的下侧分位数,可查χ2 分布分位数表(GB 4086.2)。
分布的下侧分位数,可查χ2 分布分位数表(GB 4086.2)。
以1-α 为置信度的单侧置信下限为
或
②失效率λ 的估计量。
以1-α 为置信度的双侧置信区间为
或
以1-α 为置信度的单侧置信下限为
或
③可靠度R(t0)的估计量。
以1-α 为置信度的双侧置信区间为
式中:t0——预先给定的任务时间。
以1-α 为置信度的单侧置信区间为
式中:t0——预先给定的任务时间。
(2)非替换(右侧)定时截尾寿命试验的情况(失效时间能确切测得的情况)。
对于非替换(右侧)定时截尾寿命试验的情况,欲求得严格的置信区间,在计算上相对困难。但是,可以给定简单近似的置信区间。
①平均寿命θ 的估计量。
以1-α 为置信度的双侧置信区间为:
a.当r=0 时:
b.当r=1,2,…,n-1 时:
或
c.当r=n 时:
式中:![]() 分布的下侧分位数,可查χ2 分布分位数表。
分布的下侧分位数,可查χ2 分布分位数表。
以1-α 为置信度的θ 单侧置信区间为:
a.当r=0,1,2,…,n-1 时:
或
式中:当r=0 时,Tr,n =nτ,这是没有失效试件的情况。
b.r=n 时:
②失效率λ 的估计量。
以1-α 为置信度的λ 的近似双侧置信区间为:
a.当r=0 时,由式(4-48)的界限取倒数推得
式中:τ——预先规定的停试时间。
b.当r=0,1,2,…,n-1 时,由式(4-49)和式(4-50)的界限取倒数推得
或
以1-α 为置信度的λ 的近似单侧置信区间为:
a.当r=0,1,2,…,n-1 时:
或
b.当r=n 时:(https://www.xing528.com)
③可靠度R(t0)的估计量。
因为
![]() ,可以利用θ 的单双侧近似置信区间,分别得到R(t0)的单双侧近似置信区间。
,可以利用θ 的单双侧近似置信区间,分别得到R(t0)的单双侧近似置信区间。
以1-α 为置信度的R(t0)的近似双侧置信区间可由式(4-48)、式(4-50)和式(4-51)分别得到。
a.当r=0 时:
b.当r=1,2,…,n-1 时:
或
c.当r=n 时:
由式(4-54)和式(4-55),可分别得到R(t0)的以1- α 为置信度的近似单侧置信区间。
a.当r=0,1,2,…,n-1 时:
或
b.当r=n 时:
(3)非替换定时截尾寿命试验的情况(失效时间不能确切测得的情况)。
在有的情况下,只知道在一段时间内失效的个数,不知道确切的失效时间。在现场试验中所得到的数据,很多属于这种情况。
有n 件随机抽取的试件,进行非替换的寿命试验,试验到预先规定的时间τ 停止,在此前失效个数为r。在此假定下,则可得到以下结果:
①平均寿命θ 的估计量。
以1-α 为置信度的θ 的单侧置信区间为
以1-α 为置信度的θ 的双侧置信区间为
式中:![]() 和
和![]() 2)——F 分布的下侧分位数,可查F 分布分位数表(GB 4086.4)。
2)——F 分布的下侧分位数,可查F 分布分位数表(GB 4086.4)。
②可靠度R(t0)的估计量。
以1-α 为置信度的R(t0)的单侧置信区间为
以1-α 为置信度的R(t0)的双侧置信区间为
式中:t0——预先给定的任务时间。
(4)非替换混合截尾寿命试验的情况。
对于混合截尾寿命试验的停试规则,有两个预先给定的停试指标,即可容许的失效个数r 和最长的试验时间τ。在试验过程中,只要达到一个停试指标,则寿命试验停止。也就是说,当t(r)≥τ 时,则属于非替换的定时(右侧)截尾寿命试验,在τ 以前失效个数记为r′;当t(r)<τ 时,则属于非替换的定数(右侧)截尾寿命试验。
①平均寿命θ 的估计量。
以1-α 为置信度的θ 的单侧置信区间为:
a.当t(r)≥τ 时:
式中:
b.当t(r) <τ 时:
式中:
以1-α 为置信度的θ 的双侧置信区间为:
a.t(r)≥τ 时:
式中:Tr′,n——由式(4-73)给出。
式(4-76)也就是式(4-50)的形式
b.当t(r) <τ 时:
式中:Tr,n——由式(4-75)给出。
②可靠度R(t0)的估计量。
以1-α 为置信度的R(t0)单侧置信区间为:
a.当t(r)≥τ 时:
式中:Tr′,n——由式(4-73)给出;
t0——预先给定的任务时间。
b.当t(r)≤τ 时:
式中:Tr,n——由式(4-75)给出;
t0——预先给定的任务时间。
以1-α 为置信度的R(t0)双侧置信区间为:
a.当t(r)≥τ 时:
式中:Tr′,n——由式(4-73)给出。
t0——预先给定的任务时间。
b.当t(r)≤τ 时:
式中:Tr,n——由式(4-73)给出。
t0——预先给定的任务时间。
(5)非替换定数逐次截尾寿命试验的情况。
由式(4-39)和式(4-40)可知
2.两参数指数分布
两参数指数分布比前述单参数指数分布多一个参数γ,称为起始参数,而θ 称为尺度参数,它不再代表平均寿命。
1)点估计
(1)非替换(右侧)定数截尾寿命试验的情况。
通常希望选择最小均方误差的估计量,即![]() 和
和![]() 。
。
根据上述估计量可得到可靠度
为了得到区间估计,可以选择![]() 和
和![]() 。
。
(2)非替换(右侧)定时截尾寿命试验的情况。
①尺度参数θ 的估计量。
②起始参数γ 的估计量。
(3)失效率。
2)区间估计
(1)非替换(右侧)定数截尾寿命试验的情况。
①θ 的置信区间估计。
以1-α 为置信度的双侧置信区间为
式中:![]() ——由式(4-86)给出。
——由式(4-86)给出。
以1-α 为置信度的单侧置信区间为
②γ 的置信区间估计。
以1-α 为置信度的双侧置信区间为
式中:![]() ——由式(4-86)给出;
——由式(4-86)给出;
![]() ——F 分布的下侧分位数,可查F 分布分位数表。
——F 分布的下侧分位数,可查F 分布分位数表。
以1-α 为置信度的单侧置信区间为
③失效率λ 的置信区间估计。
因为![]() ,利用式(4-91)和式(4-92)就可得到λ 的单、双侧置信区间。
,利用式(4-91)和式(4-92)就可得到λ 的单、双侧置信区间。
以1-α 为置信度的双侧置信区间为
式中:![]() ——由式(4-86)给出。
——由式(4-86)给出。
以1-α 为置信度的单侧置信区间为
④可靠度R(t0)的近似置信区间。
第一近似区间为:
以1-α 为置信度的双侧置信区间为
式中:t0——预先给定的任务时间;
![]() ——由式(4-86)给出。
——由式(4-86)给出。
以1-α 为置信度的单侧置信区间为
第二近似置信区间为:
利用标准正态分布可得到以1-α 为置信度的双侧置信区间为
式中:t0——预先给定的任务时间;
m——由式(4-98)给出。
v——由式(4-99)给出。
![]() ——标准正态分布的下侧分位数,可查正态分布分位数表(GB 4086.1)。
——标准正态分布的下侧分位数,可查正态分布分位数表(GB 4086.1)。
利用标准正态分布可得到以1-α 为置信度的单侧置信区间为
第三近似置信区间为:
利用θ 和γ 置信区间得到可靠度R(t0)的置信区间。
以1-α 为置信度的双侧置信区间为
式中:θu——由式(4-91)得到的θ 的置信上限;
θl——由式(4-91)得到的θ 的置信下限;
γu——由式(4-91)得到的γ 的置信上限;
γl——由式(4-91)得到的γ 的置信下限。
以1-α 为置信度的单侧置信区间为
式中:θl——由式(4-92)得到的θ 的置信下限;
γl——由式(4-94)得到的γ 的置信下限。
(2)有替换(右侧)定数截尾寿命试验的情况。
有关θ、γ、λ 和R(t0)的置信区间公式[式(4-91)~式(4-100)]也适用于有替换定数截尾寿命试验。所不同的是,所有非替换定数截尾寿命试验公式中的![]() 应由式(4-105)计算,即
应由式(4-105)计算,即
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




