如今,绝大部分可靠性优化分配工作集中于该领域的六大研究热点,这些研究大都仅考虑系统的一个最主要的功能,尽管提出了对有功能差异性的多功能系统可靠性指标分配方法,但上述研究仍无法综合考虑多功能可修系统的复杂特性而直接将系统可靠性指标权衡优化分配给设计单元。另外,在工程实际中,设计单元分为设计型单元和版本选择型单元,且二者在设计过程中常混合使用。因此,在考虑资源配置条件和设计单元类型的情况下,以可用度为目标对有复杂特性的多功能可修系统进行可靠性指标和维修性指标权衡优化分配,不但具有重要的工程意义,而且符合系统可靠性、维修性、指标权衡优化分配领域的研究热点。

图3-9 基于模糊层次分配和新、旧系统分配的故障率复合分配方法的流程
基于GO 法的装甲车辆可靠性、维修性指标权衡优化分配的描述如下:以多功能可修系统可用度为目标,考虑费用最小和系统复杂特性,利用系统级—功能级—设计单元级的层次结构基于GO 法建立系统约束条件和功能约束条件,进行设计单元的故障率和维修率的权衡优化分配。上述优化分配问题的描述可以归结为:约束条件和目标函数。
1.基于GO 法的装甲车辆可靠性、维修性指标权衡优化分配问题的约束条件
根据基于GO 法的装甲车辆可靠性、维修性指标权衡优化分配问题的描述,其约束条件如下:
1)设计单元故障率和维修率约束条件

式中:![]() ——设计单元u 的故障率下限、分配故障率和故障率上限;
——设计单元u 的故障率下限、分配故障率和故障率上限;
![]() ——设计单元u 的维修率下限、分配维修率和维修率上限。
——设计单元u 的维修率下限、分配维修率和维修率上限。
2)功能故障率约束条件
![]()
式中:![]() ——基于模糊层次分配和新、旧系统分配的故障率复合分配方法所得各系统功能故障率分配值;
——基于模糊层次分配和新、旧系统分配的故障率复合分配方法所得各系统功能故障率分配值;
![]() ——使用设计单元故障率和维修率的分配值,根据系统GO 图模型进行定量GO 运算所得系统功能故障率。
——使用设计单元故障率和维修率的分配值,根据系统GO 图模型进行定量GO 运算所得系统功能故障率。
3)系统可用度约束条件
![]()
式中:![]() ——系统可用度目标值;
——系统可用度目标值;
![]() ——使用设计单元各故障率和维修率分配值,根据系统GO 图模型进行定量GO 运算所得系统的可用度。
——使用设计单元各故障率和维修率分配值,根据系统GO 图模型进行定量GO 运算所得系统的可用度。
2.基于GO 法的装甲车辆可靠性、维修性指标权衡优化分配问题的目标函数
由基于GO 法的装甲车辆系统可靠性、维修性指标权衡优化分配问题的描述可知,其目标为由设计单元构成的系统费用最小。在工程实际中,设计单元有重新设计和从不同版本的旧单元中选择两种情况,本书分别将其定义为设计型单元和版本型单元。维修的目的是减少损坏带来的影响和以最少的费用获得最大的可用性,因此,本书定义新系统的总费用由对应设计单元可靠性指标的费用和对应设计单元的维修性指标的费用组成。(https://www.xing528.com)
1)费用函数
费用函数描述设计单元的费用和可靠性指标、维修性指标间的关系,它受各种人力、物力、财力的花费影响,常用的费用函数分为两类:离散费用函数和连续费用函数,包括拉格朗日型费用函数、对数型费用函数和广义成本函数等。本节构建了考虑可靠性指标和维修性指标的设计单元费用函数。
(1)版本型单元费用函数见表3-7。
表3-7 版本型单元费用函数
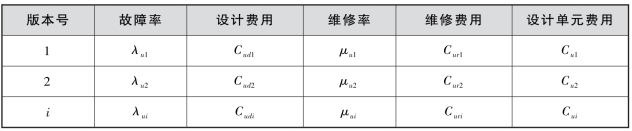
表3-7 中,λui、Cudi、μui、Curi和Cui为设计单元u 第i 个版本的故障率、设计费用、维修率、维修费用和设计单元费用,其中Cui =Cudi +Curi。(2)设计型单元费用函数,如式(3-22)所示。
![]()
式中:Cu——单元u 的费用;
fμ——根据工程实际(如零件的维修级别、维修工熟练程度和数目等)评估出的维修费用影响因子;
fλ——根据工程实际(如设计单元的材料、表面处理和加工等)评估的设计费用影响因子。
(3)对费用函数中维修费用的说明
设计型单元的维修率受其维修规划的影响,单元体维修级别一般分为:最小修理、性能恢复、换件和大修。最小修理是将单元体进行部分分解,对特定的零件进行修理;性能恢复也是将单元体进行部分分解,执行性能恢复,并稳固相关组件;大修是将单元体进行完全分解,执行最细致的工作;换件是快速修复。对于设计型单元,可以根据单元体维修级别规定其维修率的上、下限,再根据费用函数选择符合条件的单元维修率;对于版本型单元,可以根据单元体维修级别给定不同版本的维修率和相应的维修费用,也可以根据单元体维修级别规定其维修率的上、下限,在式(3-22)中可在fμ =0 的条件下根据费用函数选择符合条件的单元维修率。
2)目标函数
基于GO 法的装甲车辆可靠性、维修性指标权衡优化分配问题的目标为由设计单元构成的系统费用最小,其目标函数为

式中:minCS——系统最小总费用;
Cu——设计单元u 的费用(u =1,2,…,n)。
3.基于GO 法的装甲车辆可靠性、维修性指标权衡优化分配问题描述的数学模型
根据基于GO 法的装甲车辆可靠性、维修性指标权衡优化分配的约束条件和目标函数,相应优化分配问题的数学模型可描述为
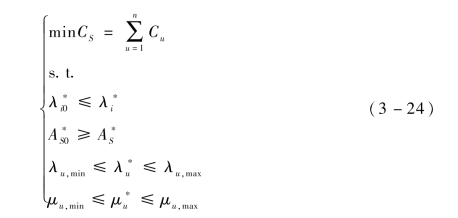
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




