组合逻辑电路的分析方法探析

1.运用逻辑函数表达式进行分析

运用逻辑函数表达时进行分析的方法，是从输入端到输出端逐级写出每一个逻辑单元的逻辑函数表达式，得出最终的逻辑函数表达式，并简化为最简形式，据此确定该电路的逻辑功能。以图3.2所示组合逻辑电路为例，该电路具有两个输入端A和B，具有4个输出端T1，Y2，Y3，Y4。各级逻辑函数表达式如下：

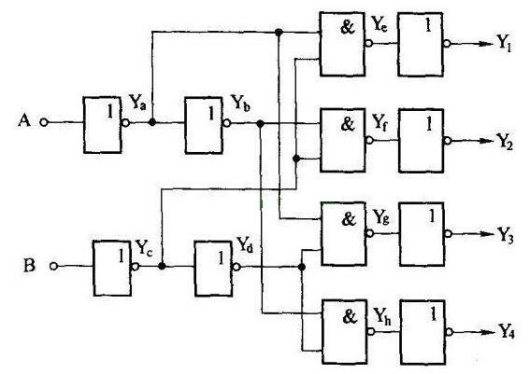
图3.2　2-4线译码器

从逻辑函数表达式可知：当输入端AB=“00”时，输出端Y1=1，当输入端AB=“10”时，输出端Y2=1，输入端AB=“01”时，输出端Y3=1，输入端AB=“11”时，输出端Y4=1。可见，这是一个2线-4线译码器，它的功能是将2位二进制码译码后，从4个输出端中所对应的哪一个输出端输出。

2.运用逻辑函数真值表进行分析

运用逻辑函数真值表进行分析的方法，是列出所有输入端与所有输出端之间的逻辑函数真值表，然后根据真值表判断出电路的逻辑功能。某组合逻辑电路如图3.3所示，它包含3个逻辑门电路D1，D2，D3，具有3个输入端A，B，C和1个输出端Y。(www.xing528.com)

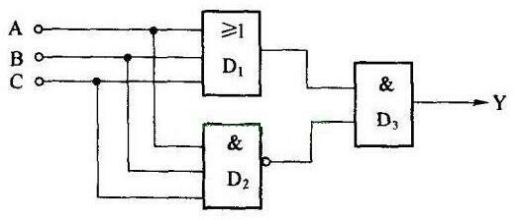
图3.3　逻辑不一致电路

3个输入端共有8种组合状态，逐一分析如下：

当ABC=“000”时，D1输出为“0”，D2输出为“1”，Y=0；当ABC=“001”时，D1输出为“1”，D2输出为“1”，Y=1；当ABC=“010”时，D1输出为“1”，D2输出为“1”，Y=1......当ABC=“111”时，D1输出为“1”，D2输出为“0”，Y=0；根据以上分析结果得到的逻辑函数真值表如表3.1所示。

表3.1　逻辑不一致电路真值表

从逻辑函数真值表可见，只有当ABC=“000”或者ABC=“111”时，才有Y=0，否则Y=1，所以，这是一个逻辑不一致电路，当三个输入端的输入逻辑状态不一致时，电路输出为1，当3个输入端的逻辑状态一致时，电路输出为0。