一、(二、八、十六进制)转(十进制)
1.二进制转十进制
方法:二进制数从低位到高位(即从右往左)计算,第0位的权值是2的0次方,第1位的权值是2的1次方,第2位的权值是2的2次方,依次递增下去,把最后的结果相加的值就是十进制的值了。
例:将二进制的(101011)B转换为十进制的步骤如下:
(1)第0位1 x 2^0=1;
(2)第1位1 x 2^1=2;
(3)第2位0 x 2^2=0;
(4)第3位1 x 2^3=8;
(5)第4位0 x 2^4=0;
(6)第5位1 x 2^5=32;
(7)读数,把结果值相加,1+2+0+8+0+32=43,即(101011)B=(43)D。
2.八进制转十进制
方法:八进制数从低位到高位(即从右往左)计算,第0位的权值是8的0次方,第1位的权值是8的1次方,第2位的权值是8的2次方,依次递增下去,把最后的结果相加的值就是十进制的值了。
八进制就是逢8进1,八进制数采用0~7这八数来表达一个数。
例:将八进制的(53)O转换为十进制的步骤如下:
(1)第0位3 x 8^0=3;
(2)第1位5 x 8^1=40;
(3)读数,把结果值相加,3+40=43,即(53)O=(43)D。
3.十六进制转十进制
方法:十六进制数从低位到高位(即从右往左)计算,第0位的权值是16的0次方,第1位的权值是16的1次方,第2位的权值是16的2次方,依次递增下去,把最后的结果相加的值就是十进制的值了。
十六进制就是逢16进1,十六进制的16个数为0、1、2、3、4、5、6、7、8、9、A、
B、C、D、E、F。
例:将十六进制的(2B)H转换为十进制的步骤如下:
(1)第0位B x 16^0=11;
(2)第1位2 x 16^1=32;
(3)读数,把结果值相加,11+32=43,即(2B)H=(43)D。
二、(十进制)转(二、八、十六进制)
1.十进制转二进制
方法:除2取余法,即每次将整数部分除以2,余数为该位权上的数,而商继续除以2,余数又为上一个位权上的数,这个步骤一直持续下去,直到商为0为止,最后读数时候,从最后一个余数读起,一直到最前面的一个余数。
例:将十进制的(43)D转换为二进制的步骤如下,如图1.4所示。
(1)将商43除以2,商21余数为1;
(2)将商21除以2,商10余数为1;
(3)将商10除以2,商5余数为0;
(4)将商5除以2,商2余数为1;
(5)将商2除以2,商1余数为0;
(6)将商1除以2,商0余数为1;
(7)读数,因为最后一位是经过多次除以2才得到的,因此它是最高位,读数字从最后的余数向前读,101011,即(43)D=(101011)B。
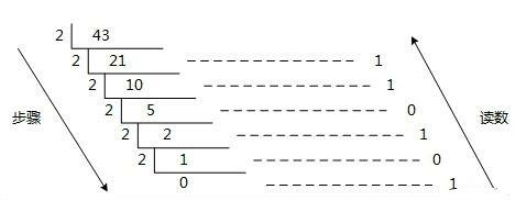
图1.4 十进制转二进制
2.十进制转八进制
方法:除8取余法,即每次将整数部分除以8,余数为该位权上的数,而商继续除以8,余数又为上一个位权上的数,这个步骤一直持续下去,直到商为0为止,最后读数时候,从最后一个余数起,一直到最前面的一个余数。
例:将十进制的(796)D转换为八进制的步骤如下,如图1.5所示。
(1)将商796除以8,商99余数为4;
(2)将商99除以8,商12余数为3;
(3)将商12除以8,商1余数为4;
(4)将商1除以8,商0余数为1;
(5)读数,因为最后一位是经过多次除以8才得到的,因此它是最高位,读数字从最后的余数向前读,1434,即(796)D=(1434)O。
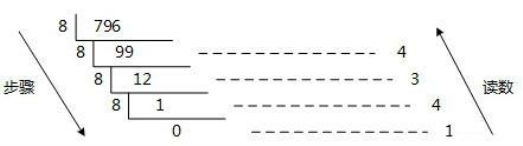
图1.5 十进制转八进制
3.十进制转十六进制
方法:除16取余法,即每次将整数部分除以16,余数为该位权上的数,而商继续除以16,余数又为上一个位权上的数,这个步骤一直持续下去,直到商为0为止,最后读数时候,从最后一个余数起,一直到最前面的一个余数。
例:将十进制的(796)D转换为十六进制的步骤如下,如图1.7所示。
(1)将商796除以16,商49余数为12,对应十六进制的C;
(2)将商49除以16,商3余数为1;
(3)将商3除以16,商0余数为3;
(4)读数,因为最后一位是经过多次除以16才得到的,因此它是最高位,读数字从最后的余数向前读,31C,即(796)D=(31C)H。
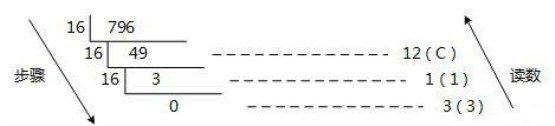
图1.6 十进制转十六进制
三、(二进制)与(八、十六进制)转换
1.二进制转八进制
方法:取三合一法,即从二进制的小数点为分界点,向左(向右)每三位取成一位,接着将这三位二进制按权相加,然后,按顺序进行排列,小数点的位置不变,得到的数字就是我们所求的八进制数。如果向左(向右)取三位后,取到最高(最低)位时候,如果无法凑足三位,可以在小数点最左边(最右边),即整数的最高位(最低位)添0,凑足三位。(https://www.xing528.com)
例:将二进制的(11010111.0100111)B转换为八进制的步骤如下,如图1.7所示。
(1)小数点前111=7;
(2)010=2;
(3)11补全为011,011=3;
(4)小数点后010=2;
(5)011=3;
(6)1补全为100,100=4;
(7)读数,读数从高位到低位,即(11010111.0100111)B=(327.234)O。
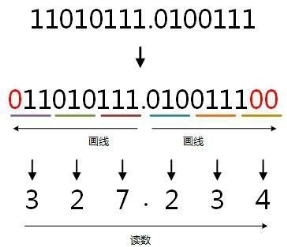
图1.7 二进制转八进制
2.八进制转二进制
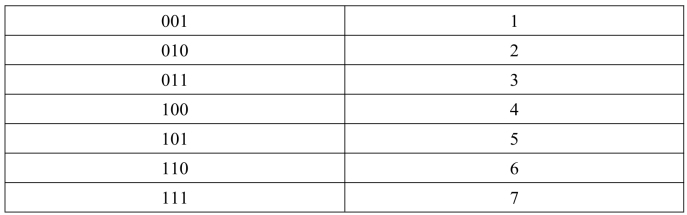
方法:取一分三法,即将一位八进制数分解成三位二进制数,用三位二进制按权相加去凑这位八进制数,小数点位置照旧。二进制与八进制对照如表1.1所示。
表1.1 二进制与八进制对照

例:将八进制的(327)O转换为二进制的步骤如下,如图1.8所示。
(1)3=011;
(2)2=010;
(3)7=111;
(4)读数,读数从高位到低位,011010111,即(327)O=(11010111)B。
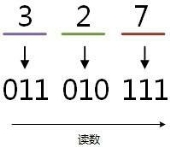
图1.8 八进制转二进制
3.二进制转十六进制
方法:取四合一法,即从二进制的小数点为分界点,向左(向右)每四位取成一位,接着将这四位二进制按权相加,然后,按顺序进行排列,小数点的位置不变,得到的数字就是我们所求的十六进制数。如果向左(向右)取四位后,取到最高(最低)位时候,如果无法凑足四位,可以在小数点最左边(最右边),即整数的最高位(最低位)添0,凑足四位。
例:将二进制的(11010111)B转换为十六进制的步骤如下,如图1.9所示。
(1)0111=7;
(2)1101=D;
(3)读数,读数从高位到低位,即(11010111)B=(D7)H。

图1.9 二进制转十六进制
4.十六进制转二进制
方法:取一分四法,即将一位十六进制数分解成四位二进制数,用四位二进制按权相加去凑这位十六进制数,小数点位置照旧。
例:将十六进制的(D7)H转换为二进制的步骤如下,如图1.10所示。
(1)D=1101;
(2)7=0111;
(3)读数,读数从高位到低位,即(D7)H=(11010111)B。
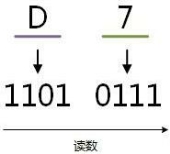
图1.10 十六进制转二进制
四、八与十六进制转换
1.八进制转十六进制
方法:将八进制转换为二进制,然后再将二进制转换为十六进制,小数点位置不变。
例:将八进制的(327)O转换为十六进制的步骤如下,如图1.11所示。
(1)3=011;
(2)2=010;
(3)7=111;
(4)0111=7;
(5)1101=D;
(6)读数,读数从高位到低位,D7,即(327)O=(D7)H。
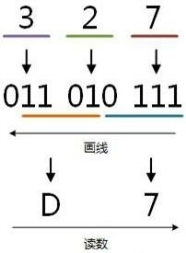
图1.11 八进制转十六进制
2.十六进制转八进制
方法:将十六进制转换为二进制,然后再将二进制转换为八进制,小数点位置不变。
例:将十六进制的(D7)H转换为八进制的步骤如下,如图1.12所示。
(1)7=0111;
(2)D=1101;
(3)0111=7;
(4)010=2;
(5)011=3;
(6)读数,读数从高位到低位,327,即(D7)H=(327)O。
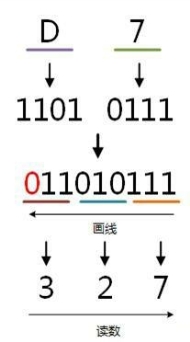
图1.12 十六进制转八进制
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




