三辆车形成三角队形的优化策略

1.三车整体平移和绕中心的转动

三个机器人正三角形编队平移运动时，机器人各自的速度与整体的速度一致。三个机器人整体绕中心点C转动，整体速度为（0，0，ω）T，三个机器人的编号及坐标系如图8-3所示。设两车中心间距为l，则机器人中心到整体中心C的距离三个机器人的速度方向与坐标轴的夹角依次为α1=60°，α2=180°，α3=300°。通过求解几何关系，可以得到三个机器人的速度分别为

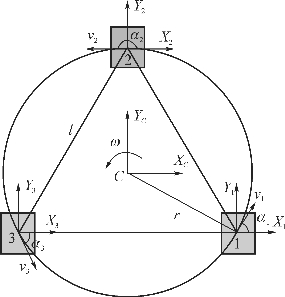
图8-3　三车正三角形编队绕中心旋转

2.三车整体绕平面任一点的转动

三车正三角形编队绕任一点的转动如图8-4所示，圆心O到整体中心C的距离为R，整体速度为（ωR cosα，ωR sinα，ω）T。设三个机器人各自速度为（ωR1cosα1，ωR1sinα1，ω）T、（ωR2cosα2，ωR2sinα2，ω）T和（ωR3cosα3，ωR3sinα3，ω）T，其中R1、R2、R3分别为机器人中心到O的距离。根据余弦定理可以得到：(www.xing528.com)

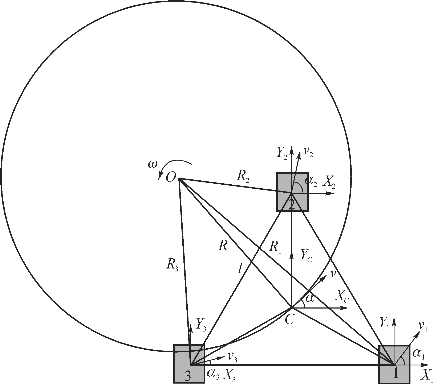
图8-4　三车正三角形编队绕任一点转动

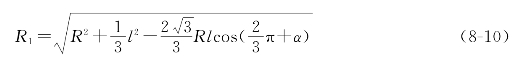
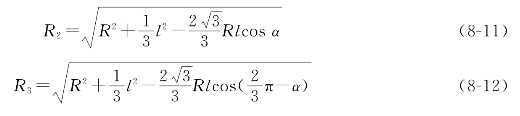
根据几何关系求解三角形可以得出α1、α2和α3的三角函数值，进而可以求出三个机器人的速度分别

如果将机器人整体的运动分解成速度为（ωR cosα，ωR sinα，0）T的平移运动和速度为（0，0，ω）T绕整体中心的转动。这两种运动为三车的基本运动形式，根据之前的讨论可以得出这两种情况下三个机器人的速度，经过速度合成就可以得出绕O点转动的三个机器人的速度为因此，经过运动分解得到的机器人的速度显然与通过几何计算得到的结果是一致的，并且计算复杂度大大降低。