Clothoid曲线的拟合方法

设C（K、γ）为一条Clothoid曲线，曲线的参数方程定义为：

其中，K为Hometetical因数，与曲线的尖锐度σ有关的参数，满足是与曲线切向角θc有关的参数，满足从曲线的参数方程可得，Clothoid曲线是无法求出解析解的，所以在生成曲线时只能采用多点近似的数值解实现。

根据Clothoid曲线的特性，曲线的曲率会随着曲线长度的大小成比例变化（图7-10），满足长度、曲率与曲线方程中的两个参数K、γ的关系分别为：

图7-10　Clothoid曲线拟合

与贝塞尔曲线一样，通常Clothoid曲线拟合采用两段对称Clothoid曲线拼接实现，使得曲率由零到最大再变为零的平滑过渡。Clothoid曲线的设计参数为第一段曲线的进入角θA、转向角θCA、曲率κA、尖锐度σA，第二段曲线的进入角θB、转向角θCB、曲率κB、尖锐度σB。给出这些参数的数值后，保证第一段曲线的终止点与第二段曲线的起始点处的曲率相同就可生成拟合曲线。

当拟合曲线过渡所需要转过的角度θCB-θA或者曲率限制很大时，两条对称Clothoid曲线是无法实现的，中间需要一段圆弧过渡区补偿较大的转向角，这样两段Clothoid曲线经过的转向角就变得小很多了。

如图7-10所示，对于Clothoid曲线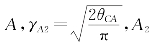点的曲率为对于Clothoid曲线点的曲率为为了达到曲率平滑过渡的效果，曲率呈线性增长的关系，也就是是一个常数。根据公式可得，在匀速运动的情况下，尖锐程度σ也是一个常数，这样曲线的设计就容易多了。圆弧段的曲率半径需满足圆心角θΩ=θB-θA-θCA-θBA。这样各段曲线的特性参数就都确定了。(www.xing528.com)

根据机器人的几何尺寸，还需对设计的曲线加一个几何约束的限制。C1点为运动过程中机器人离障碍物最近的一个点，所以要满足条件：

因此Clothoid曲线拟合的设计过程如下：

（1）根据之前计算的通过性问题确定机器人能通过的最大曲率κmax。令

（2）选择一组尖锐度σA、σB，根据公式求出Hometetical因数K、γA2、γB2，进而求出A2、B2点处的转向角θCA、θCB。

（3）根据Clothoid曲线参数方程求出A2、B2点的坐标。

（4）圆弧曲率已知，求出弦长，利用余弦定理求出圆心角θΩ，验证圆心角θΩ=θB-θA-θCA-θBA是否满足，不满足条件返回到步骤（2）重新选择一组数据。

（5）验证是否满足，不满足条件返回到步骤（2）重新选择一组数据。

（6）因曲率的线性变化，按照比例选取一系列的曲率值，利用数值解的方法确定这些点的坐标拟合出Clothoid曲线。

所以，曲线设计过程中的重要步骤就是选取合适的尖锐度σA、σB。如前分析曲线的曲率是线性增长的，尖锐度σA、σB都是常数，所以当求出的θΩ角大于或者小于要求值时，σA、σB也按照规律相应地变化。