【摘要】：圆弧拟合是最常用的曲线拟合的方法，也是最容易生成实用的方法。已知条件为：圆的起始点坐标为A1，设圆心坐标为，因此圆弧的方程可写为：如图7-8所示方程可改写为参数形式为：图7-8圆弧曲线拟合所以在曲线上任意一点处的切线斜率为：圆弧与第一段直线在A1点相切，所以必须满足-cot=k1，得到t1=arccot（-k1）。代入圆弧的参数方程可得条件：再结合曲率半径为R，求出xo、yo。圆弧的曲率半径应考虑通过性问题中的最大曲率情况，满足的条件。
圆弧拟合是最常用的曲线拟合的方法，也是最容易生成实用的方法。圆的方程形式简单，而且曲率保持恒定的特性使其设计起来很容易。
已知条件为：圆的起始点坐标为A1（x1，y1），设圆心坐标为（xo，yo），因此圆弧的方程可写为：
如图7-8所示方程可改写为参数形式为：
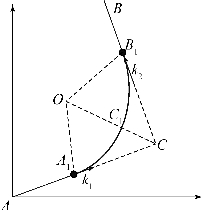
图7-8 圆弧曲线拟合
所以在曲线上任意一点处的切线斜率为：
圆弧与第一段直线在A1点相切，所以必须满足-cot（t1）=k1，得到t1=arccot（-k1）。代入圆弧的参数方程可得条件：(www.xing528.com)
再结合曲率半径为R，求出xo、yo。
根据出弯时要求的切线斜率k2，满足-cot（t2）=k2，可得t2=arccot（-k2）可确定B1点的坐标（xo+R cos t2，yo+R sin t2），出弯后由斜率k2的直线连接。
式中，斜率k1、点A1（x1，y1）都是已知条件，唯一需要确定的参数就是圆弧半径。圆弧的半径的大小决定了设计曲线的长短、形状，所以需选取一个合适的值。圆弧的曲率半径应考虑通过性问题中的最大曲率情况，满足
的条件。同时根据机器人的几何参数约束，在通过圆弧的过程中，圆心O（xo，yo）与障碍物C（xc，yc）的交点C1（xc1，yc1）是距离障碍物最近的点。满足
代入前述式子可得：
所以圆弧半径需满足的两个条件为：
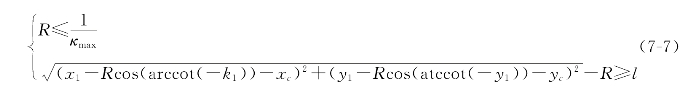
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
