机器人循迹实验的结果分析

针对前文讨论的路径跟踪与路径规划的一系列问题，实验环节主要就机器人使用的双目视觉反馈系统的控制算法能否沿封闭路径循迹和循迹的效果、不同的循迹方法产生的效果比较、PID控制参数的调节对系统的影响、通过性约束条件的作用、曲线特征参数的不同产生的效果等方面展开讨论。

1.机器人沿封闭路径循迹

将机器人沿封闭的路线循迹前进，可用于测试机器人循迹算法和稳定性控制方法的实用性。三个全方位移动机器人分别沿着各自设定好的封闭轨迹实现循环重复的循迹功能，选择一组经PID调整后能够完整跑完一圈并不偏出轨道的控制参数，使得机器人能够稳定实现循迹功能。在循迹过程中，分别记录每个机器人前后相机每个周期处理的偏距、偏角信息，分析机器人的偏距的变化幅度，评价机器人循迹的效果。

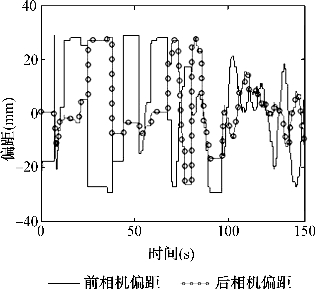
图6-14至图6-19为三个机器人循迹过程中前、后偏距随时间变化的曲线。两个小机器人的循迹前进速度为0.3 m/s，从图6-14、图6-15中可以看出，白色的机器人的前后偏距值都在±20 mm之间变动，可见机器人不断地进行偏距的修正，实现稳定的循迹功能。三个机器的前相机的偏距图中出现了一次超过30 mm的偏距，明显是偏距突变的情况，产生的原因很可能是相机反馈的数据在传输过程中出现了误码，因此，在反馈数据的处理上，需考虑容错和剔除错误数据的算法。

图6-14　图6-8中的白色机器人前相机偏距变化图

图6-15　图6-8中的白色机器人后相机偏距变化图

蓝色机器人循迹的效果与白色机器人几乎是一样的，偏距都在一定的范围内上下跳动，偏距的最大值稍大于白色的机器人（图6-16、6-17）。

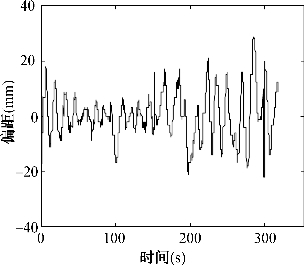
图6-16　图6-9中的蓝色机器人一整圈前相机偏距变
化

图6-17　图6-9中的蓝色机器人一整圈后相机偏距变化

大机器人的偏距图在偏距变化上都呈现出不同的幅度，原因是机器人所经过的路段不同，在圆弧较大处的偏距变化很小，遇到S弯时偏距的变化就会大一些，震荡也明显（图6-18、图6-19）。

图6-18　图6-10中的大机器人一整圈前相机偏距变化图

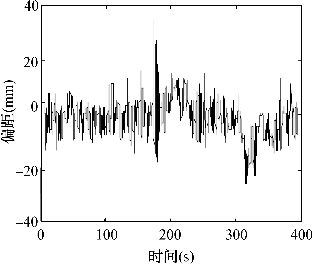
图6-19　图6-10中的大机器人一整圈后相机偏距变化图

另外，本文对于PID控制加入机器人循迹的算法中的实验效果也作了一些数据分析，并将PID算法与PD算法的效果作了一个对比，如图6-20、图6-21所示。

图6-20　蓝色机器人一整圈前相机偏距变化

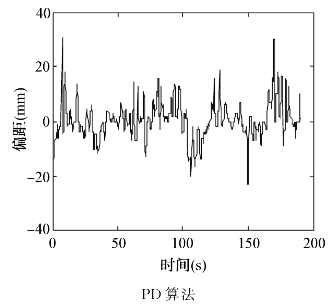
图6-21　蓝色机器人一整圈后相机偏距变化

就循迹的实现效果来说，两种算法都能稳定地保证机器人沿着预定轨迹自动导引，偏距的变化范围也几乎没什么区别。唯一有区别的是平均偏差值，PID算法的值明显要小，这也体现了积分环节消除静差的作用（表6-3）。

表6-3　PD算法与PID算法的相机偏距比较

2.不同的循迹方法对循迹结果的影响

本文讨论了两种实现机器人路径跟踪的方法，分别为使用偏距和偏距、偏角结合。本文使用蓝色的机器人作为实验对象，用两种方法分别循迹同一段路线（一条直线加一个弯道），记录相机反馈的偏距和偏角值，分析两种方法循迹的区别和优缺点。

从图6-22、6-23得出，第一种方法由于只根据偏距的信息修正机器人偏离轨迹的幅度和姿态，所以偏距的修正是比较及时的，而偏角在经过圆弧的过程中，没有修正的变化，反映的就是当前机器人的姿态，所以在到达直线路段后偏角才变为零；第二种方法偏距和偏角的修正都加入算法中，偏角是有修正的，但是相对的偏距由于偏角修正的关系变化得很厉害（图6-24、图6-25）。基于对机器人循迹的要求标准而言，考察的关键是机器人不能偏离预定的轨道，所以第一种方法的循迹效果要更好一些。

3.PID参数调节对循迹结果的影响

PID参数调节是机器人循迹稳定性控制的重要环节，只有合适的参数才能保证机器人能够实现循迹功能。

本实验机器人采用的是PD控制的方法，关键在于控制比例参数P。图6-26至图6-29为不同的比例参数情况下前后偏距的变化情况，最终确定了一个比较合适的比例参数为0.0029。当比例参数较大时，偏距的纠正变化震荡剧烈，当震荡过大时就会偏离轨迹；当比例参数过小时，偏距的纠正幅度很小，跟不上机器人循迹的动作，偏距会越来越大，无法及时修正，最终偏离轨道。

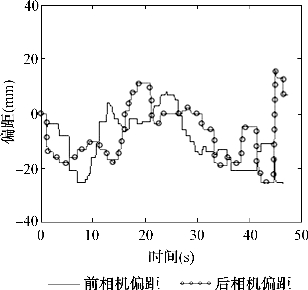
图6-22　蓝色小车第一种算法偏距变化图

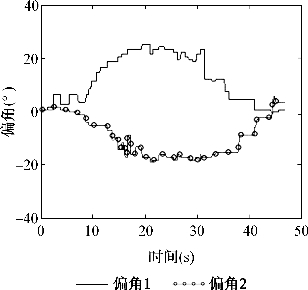
图6-23　蓝色小车第一种算法偏角变化图

(www.xing528.com)

图6-24　蓝色小车第二种算法偏距变化图

图6-25　蓝色小车第二种算法偏角变化图

图6-26　白色小车kp1=0.01

图6-27　白色小车kp1=0.1

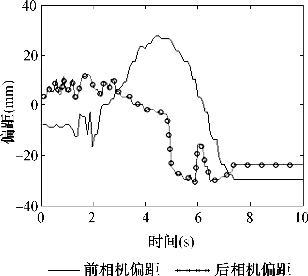
图6-28　白色小车kp1=0.05

图6-29　白色小车kp1=0.0029

图6-30　白色小车kp1=0.0029 kd1=10

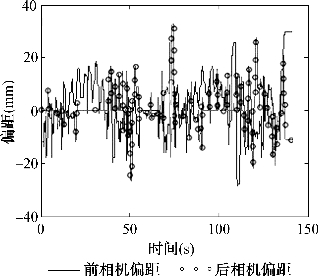
图6-31　白色小车kp1=0.0029 kd1=0.1

比例参数调节完成后，微分环节主要是控制偏距调节的频率和速度，如图6-30所示，当参数值很大时偏距的变化频率很快，说明此时机器人的头部在不停地左右摆动，这种不稳定性是需要处理的。因此取了一个较合适的值0.1后，循迹的效果相比较不加微分参数的情况还要好一些，如图6-31所示。

4.机器人运动约束的循迹效果

本实验讨论的是不同尺寸的机器人以不同的速度沿不同的圆弧曲线循迹效果的对比，结合之前讨论的考虑几何约束、运动约束的公式，分析机器人循迹的效果。

在机器人以不同的速度走过同一个大小的弯时，明显速度越小，偏距的变动幅度越小，机器人走得越稳，如图6-32、图6-33所示，虽然在速度为0.15 m/s、0.1 m/s的时候有两个偏距突变值，但是总体的变化幅度还是符合推导的公式的关系。

5.机器人几何约束与不同曲线的特性参数的循迹效果

将机器人以相同的速度沿着不同的曲率半径的圆弧进行循迹测试，目的是分析曲率的不同对机器人循迹效果的影响，以及机器人的尺寸的影响。实验过程中记录前后相机反馈的偏距值得到如下的几张变化图（图6-34～图6-36）。

图6-32　白色机器人不同速度走同一个弯的前相机偏距变化图

图6-33　白色机器人不同速度走同一个弯的后相机偏距变化图

可以明显地看出转弯半径越大，对于机器人来说循迹的难度就越小。如图6-35所示，前后偏距的变化都很小，机器人运动得很稳定；而半径小了一些后，在相同的条件下机器人的循迹效果没有那么好，偏距的变化也更剧烈一些，这也与先前推导的公式结论是相符合的。

图6-34　白色小车走半径为1米的圆弧

图6-35　白色小车走半径为1.5米的圆弧

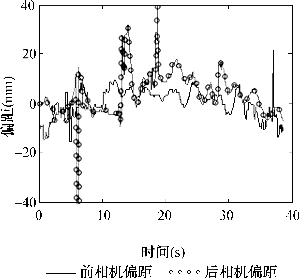
图6-36　白色小车走半径为1.2米的圆弧

图6-37　白色小车走不同斜率的折线

对于机器人走不规则折线的情况，在循迹轨道上铺设了由不同斜率组合而成的直线，主要用于分析从一条直线到另一条直线过程中出现不同角度的变化时的循迹效果。由图6-37可看出，在机器人到达直线的过渡点时，由于循迹路线的突变，偏距都有一个明显的增加，待达到稳定后都能顺利地继续走下去。对于变动幅度小的情况，循迹的效果好，偏距的变化小。另外，并不是所有弯折幅度都能通过，经测试，机器人在接近两线偏角35°的时候达到临界状态。

本章主要研究Mecanum轮全方位移动机器人双相机视觉循迹方法及工程实现。采用双相机视觉分别检测机器人前后两端位置测量点与参考路径的偏差，建立Mecanum轮机器人的双相机循迹运动误差模型，设计了循迹系统的误差修正算法，通过模糊控制和基于运动学模型的控制方法，实现了对预定路径的有效跟踪和稳定运行。