循迹曲线参数的约束条件

除了机器人的几何参数、运动学和动力学约束外，轨迹曲线的参数特征也和通过性条件有很大关系，相关联的参数有：曲线的切向量的变化率曲线在各位置的曲率大小κ；曲率的变化率（曲线在每个位置切线方向的角度变化），说明的是曲线的尖锐程度。弧长变化率与曲线曲率大小对机器人循迹的影响是与机器人的运动学约束等综合考虑的，之前已经详细讨论过了。在这一小节讨论的是对于一些特殊的曲线，机器人循迹的通过性问题。

斜率不连续通常出现在线段与线段之间的交点处、圆弧与圆弧的交点处、线段与圆弧的交点处。

1.循迹曲线为折线

考虑两段不同斜率的线段组成的折线情况，设两段直线l1、l2的斜率分别为k1、k2，所以两条直线的夹角为arctan（k2）-arctan（k1），折点处坐标为（x'，y'），得到两条直线的方程为y1=k1x1+y'-k1x'、y2=k2x2+y'-k2x'。机器人前进的速度为vy，依然采用PID控制算法和偏距校正的原理实现循迹功能。机器人前进方向的斜率为k，未调整时前相机位置处的坐标为（x″，y″），调整后的前相机位置坐标为（x‴，y‴），初始位置为（x'，y'），位置坐标在不断变化。机器人与直线l2的夹角θ'是在不断调整变化的，前进方向的初始值为k1。

每一次的调整过程，机器人都沿前进方向走了距离l=vyΔt，产生了新的偏距偏角需要调整。

未调整时前相机位置处的坐标为（x″，y″）的计算公式为：

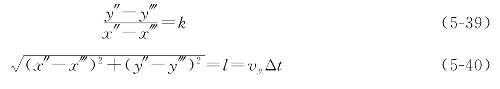
（x‴，y‴）为上一次调整过后的前相机位置。

因此前进轨迹的直线方程为y=kx+y″-kx″。过直线l2上的点A（a，b）与点（x″，y″）的连线垂直于机器人的前进路线，A（a，b）的值可由公式确定：

因此前相机得到的新偏距值为后相机还在前一条直线上，偏距很小为d2。经过PID算法调整后，前相机的偏距变为：

此时机器人与目标直线的夹角变为：

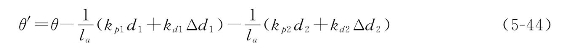
调整后机器人前进轨迹的斜率k可由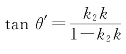确定新的位置，调整后的前相机的位置坐标变为：

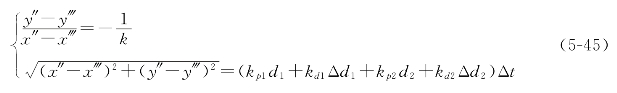
这样机器人的一次调整就完成了，如此循环调整直到机器人头部调整到达了直线l2。在调整过程中，根据要求经过PID算法调整后的偏距、偏角必须满足条件，调整PID参数：(www.xing528.com)

后相机经过折点后的运动调整与前相机是相同的，计算方法可参照前相机。

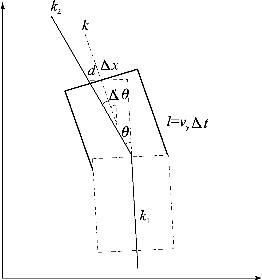
图5-8　循迹线为折线

实际上，机器人经过折点后的第一次调整对机器人能否通过有很大的影响。此时，前相机与直线l2的偏距为vyΔt·tanθ，经过调整后的偏距为：

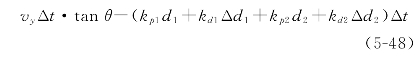
所以，在相同的参数下，折线的斜率变化越大、机器人的运动速度越快，调整后的偏距就越大，就越容易偏离预定轨迹（图5-8）。

2.循迹轨迹为不规则曲线

讨论的另一个问题是曲线的曲率变化率，研究的就是不规则的曲线。这类曲线的一个特点就是曲率不连续。例如在曲线与曲线的交界处，就会出现曲率不连续的情况。

根据曲率的计算公式，求导可得：

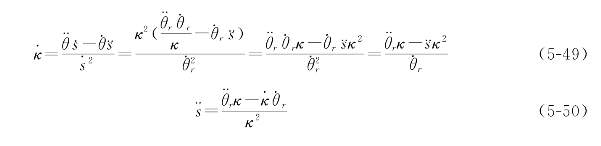
求导可得：

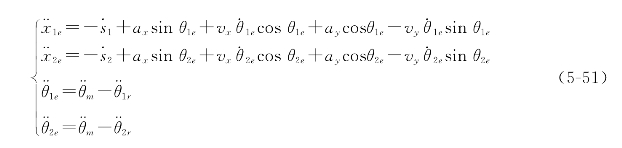
代入可得：

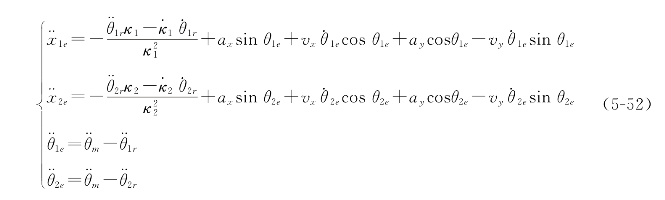
这样就得到了曲率变化率与其他的参数之间的关系，以及对机器人循迹的影响。从公式可以看出，曲率的变化率与加速度有很大的关系，会影响机器人的行进加速度、曲线切向量的变化快慢。