机器人动力学约束优化方案

机器人在循迹过程中的前进速度vy是保持恒定的，所以这里讨论的加速度问题为横移加速度ax和旋转角加速度αz。这两个加速度是由于偏距、偏角的PID算法产生的。

对式（5-26）求导可得加速度的关系表达式：

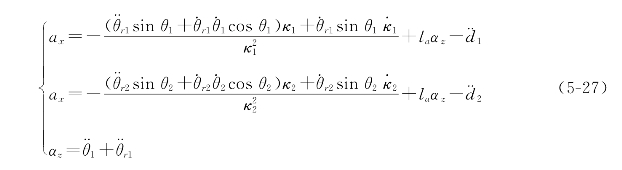
式（5-27）对于机器人横向加速度、转动加速度有了运动限制。

机器人的动力学问题除了考虑机器人在循迹过程中是否有能力做出相应的调整姿态，还必须根据电机性能对每个轮子的动力学性能进行分析，当电量下降使得电机加速性能有所降低时，相应可实现的加速度就肯定有限制，能做出的误差修正的幅度也就越小。

根据机器人的运动学模型，得到整车加速度与轮子加速度的公式：

根据机器人的动力学方程可得到车轮扭矩与轮加速度、轮速的关系：

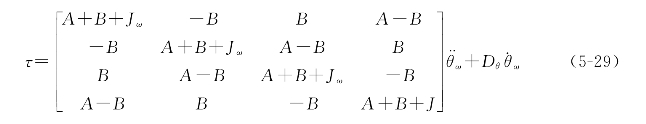
其中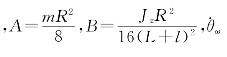代表了各轮的速度大小，由机器人的运动学模型推出，代表轮子的角加速度。这样机器人的加速度ax、αz与每个电机提供的扭矩τ联系起来。

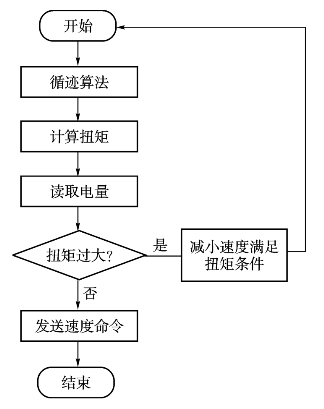
电机的性能不同，运动中电机能够产生的扭矩则不同，设τ［］为能够允许的最大扭矩，在速度没有变化的情况下，循迹算法的调整幅度将受到τ［］的约束。所以当扭矩不够时，需相应调整前进速度的大小，这样才能保证机器人有能力调整循迹的姿态（图5-7）。

同样，机器人采用的驱动方式为电驱动，使用的是电池箱。从电量充满的时刻起，能量逐渐消耗，根据功率、转速、扭矩的公式可以得到，可提供的驱动扭矩也是逐渐减少的。设驱动扭矩可提供的最大值为τ'［］，与电机提供的最大扭矩不同的是，τ'［］将随电量的改变而逐渐减小，机器人的循迹能力也是不断变化的。

根据动力学约束条件，在循迹算法中需要考虑动力学因素，动力学参数的获得难度并不相同。相对来说电量获得的方法简单，只需通过模拟量采集。因为电量产生的动力学参数变化是在运动过程中时刻发生的，所以只考虑这个因素也是可以的。

(https://www.xing528.com)

图5-7　扭矩控制方法框图

循迹算法流程：在上述讨论的基础之上，考虑加速度约束与PID参数结合的情况下机器人的加速度的大小是由偏距、偏角经过PID算法计算之后得到的。

对于第一种循迹算法：

对于第二种循迹算法：

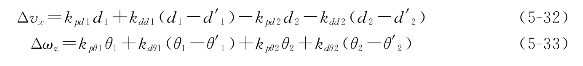
加速度由循迹算法得到，对于第一种循迹算法：

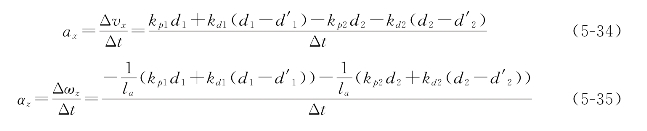
对于第二种循迹算法：

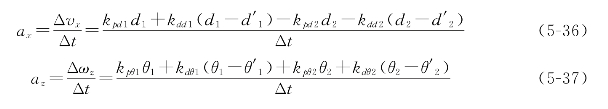
再由式（5-36）、（5-37）讨论的加速度约束条件就能得到PID参数调整的影响。