最小转弯半径优化技巧

对于理想情况，由于安装在机器人前后的相机需同时看到地面上的循迹线，所以对于半径为R的圆弧，考虑极限情况前后相机分别在圆弧与其他线段的交点处。此时，前后相机的连线长度就是圆弧的直径2R，最小转弯半径为机器人的两相机距离的一半la。

在循迹过程中，允许机器人沿轨道前进有一定的偏差，设这个偏差为d1、d2。一般情况有4种：d1＞0、d2＞0；d1＞0、d2＜0；d1＜0、d2＞0；d1＜0、d2＜0。对于d1＞0、d2＜0的情况，机器人的前后端均处于循迹轨迹的内沿，最小转弯半径没有变大，仍为la。当d1＜0、d2＞0时，机器人的前后端均处于循迹轨迹的外沿，最小转弯半径为la+d1+d2。当d1＞0、d2＞0，d1＜0、d2＜0时，机器人的前后端分别在曲线的两侧，此时最小转弯半径都不会超过la+d1+d2。所以，在一定的误差允许范围内，机器人的最小转弯半径可有所增加。

上述讨论的最小转弯半径并没有考虑机器人运动特性的影响，在速度趋近于零时的极限情况，最小转弯半径可达到la，在考虑循迹误差的情况下，可达到la+d1+d2。但是机器人在以速度v匀速前进的过程中，一旦在某一时刻由于速度过快没有及时调整偏离轨道，机器人就会停止运动，同时每一时刻的偏差值也不同，调整的结果也不同。因此，机器人的最小转弯半径还跟速度和误差调整的快慢有关。运动过程中的机器人的最小转弯半径问题可以等价为求循迹曲线的最小转弯半径，也就是最大曲率的问题。

设定Δt为一个运动周期，在这个运动周期里，由控制器接收反馈的偏距、偏角信息，计算机器人当前的运动速度，发送给每一个轮子使得机器人按预定要求前进。根据第二章推导的运动学模型，可得：

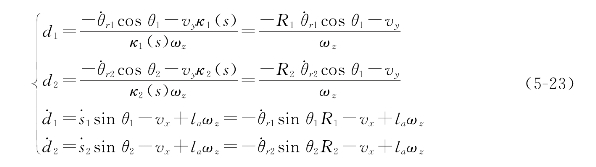
d1、d2为当前前后相机检测到的偏距为偏距的变化率，vy为机器人前进速度，ωz为旋转速度，θr1、θr2代表前后相机对应的曲线位置处的切向量变化率。值得注意的是对于图5-3所示情况为负值，所以这两项实际为正值。(www.xing528.com)

因此，要求运动过程中的机器人的最小转弯半径，只需求出R1（s）、R2（s）中较小一个。可以看出机器人实际的最小转弯半径并不是一个固定的值，是一个动态的值，与机器人当前的前进速度、横向速度、转动速度以及偏距、偏角一系列因素有关。

推导可得运动过程中的最小转弯半径为：

在循迹过程中，通常会设定一个允许的偏差值dmax、偏角θmax。偏距的变化率要尽量小，满足，代入公式中就可得到理论情况最大的最小转弯半径。

循迹过程中的最小转弯半径决定了机器人路径跟踪时能通过的轨迹的特征，为路径规划提供了理论依据。