以跟踪曲线为基准的误差调整运动学模型优化

这种运动学模型考虑的是机器人沿跟踪轨迹前进时，机器人相对于跟踪曲线的偏差，也就是以跟踪曲线为基准的误差调整模型。这种模型是在跟踪曲线所处的坐标系中讨论的。

如图5-2所示，y Ox为与地面固连的绝对坐标系，Px'y'为与机器人固连的坐标系，与绝对坐标系夹角为θm（图中θm的值为负）。机器人中心点为P，vx、vy、ωz分别为机器人在Px'y'坐标系中的x向速度、y向速度、旋转速度。v为机器人的绝对速度（实际运动方向），数值上在绝对坐标系中的矢量角为θt。

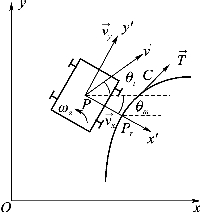
图5-2　全方位移动机器人路径跟踪的运动模型

曲线C为机器人需要跟踪的曲线，曲率为κ（s），Pr为当前机器人的理论位置。为曲线在Pr点的切向量，与x轴夹角为反映了机器人与预定轨迹的偏角。

在上述模型中，考虑了机器人路径跟踪的误差，只要满足误差有收敛的趋势，那么机器人就可以实现路径跟踪。我们考虑的误差定义为：

xe：P（xm，ym）与Pr（xr，yr）在x向的偏差；

ye：P（xm，ym）与Pr（xr，yr）在y向的偏差；(www.xing528.com)

θe：机器人实际运动方向与曲线切线方向的夹角。

将误差变换到Frenet坐标系中，也就是跟踪曲线所在的坐标系，我们就可得到循迹过程中沿曲线方向和法线方向的误差，可得：

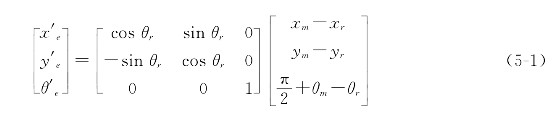
忽略ye方向的误差，只考虑沿曲线法线方向的误差和姿态误差的情况下上式可简化为：

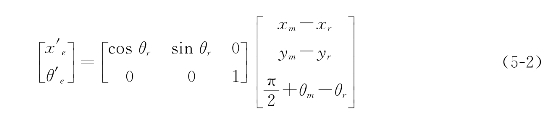
对xe、θe求导得：

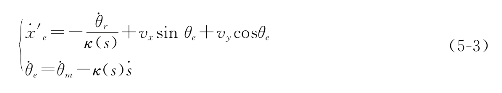
公式（5-3）为机器人路径跟踪时的控制量与机器人运动学参数之间的关系表达式。