由其逆运动学方程可知,Mecanum轮全方位移动机器人的整体运动是由其结构参数和四个车轮的速度控制的。而由于车轮惯性、地面不平以及其他种种因素的影响,各个电机输出的实际转速与理论转速之间有一定的偏差,该偏差会导致车体整体运动的实际速度与理论转速不一致,进而影响整车运动精度。因此,Mecanum轮全方位移动机器人的结构参数和四个车轮速度的控制精度对整车的运动精度极为重要。本节主要研究其结构参数及四个车轮的运动控制精度对Mecanum轮全方位移动机器人的位移精度的影响。
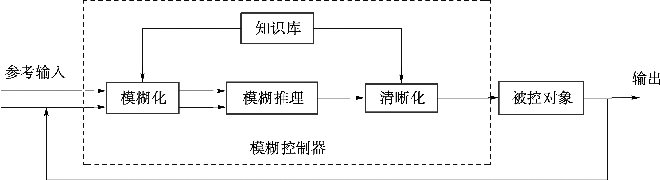
图4-4 模糊控制器基本结构
设控制移动位移为s,位移误差取Δε,并记Mecanum轮全方位移动机器人的实际速度和位置分别为V t()、P t(),即
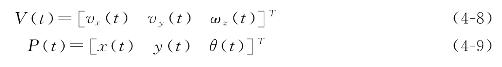
若将全方位移动机器人的车体Σv坐标系中的坐标参数全部转换到世界坐标系Σ中,可得到:

结合式(4-8)~(4-10),得:
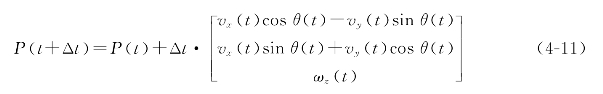
记函数f P,V,t()表示式(4-11)右边项,则上式可近似表示为
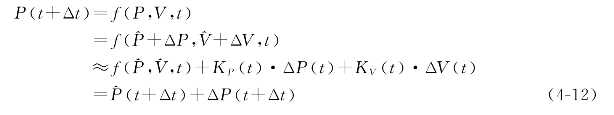
其中,
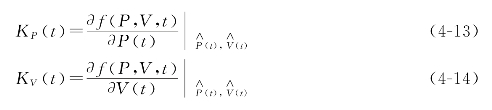
于是,运动误差可表示为:
![]()
由式(4-15)可知,系统的运动误差是由实际采样时间内的位置和速度误差累积而成。为达到实际控制要求,现对相关量进行分析。
1.机器人结构参数误差对其运动的影响
由第三章公式(3-17)知,当电机速度一定时,机器人的运动的速度误差可表示为
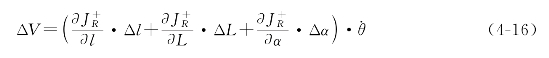
其中,
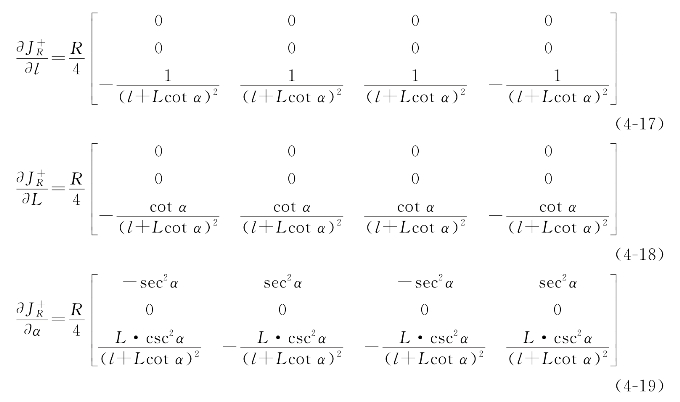
由式(4-16)~(4-19)可知,Mecanum轮全方位移动机器人的结构误差中,长宽参数的误差只对机器人的原地旋转运动有影响,而对机器人的直线运动不产生影响,也就是说机器人的直线运动变成了原地旋转和直线运动的合成运动;Mecanum轮的辊子轴线与轮毂轴线之间的夹角α则对机器人的横向运动、原地旋转运动有影响,而对机器人的纵向运动不产生影响。
由上述分析可得,在直线运动时,由于夹角α对于横向和纵向的影响不同,势必使得最后的合成运动偏离原来的位置。为减小α对机器人平动产生的影响,可以通过对其的标定来实现。
具体标定方法如下:
由于机器人的长宽参数误差对机器人的旋转运动有影响,如果通过对机器人的原地旋转运动进行标定来减小运动误差的话,势必引入新的误差。故而,为减小标定误差,现只通过对横向运动(x轴)的运动分析来对机器人进行速度标定。Mecanum轮全方位移动机器人横向运动的期望速度![]() ,实测速度
,实测速度![]()
![]() ,两式相比得:
,两式相比得:

只需测得机器人横向运动的实际速度,由横向理论速度vxd与理论夹角αd就可得到α的实际值αr。这样,在进行运动学计算的时候将αr带入运动学方程,就可以有效地减小运动误差。
2.电机转速误差对机器人运动的影响
记各个电机输出的实际转速为![]() ,将
,将![]() 处展开,略去高阶项,得
处展开,略去高阶项,得![]() ,即
,即
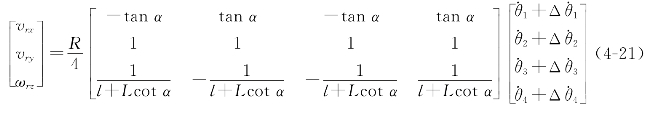 (https://www.xing528.com)
(https://www.xing528.com)
于是,机器人各个方向的实际速度与期望速度之间的关系可描述为
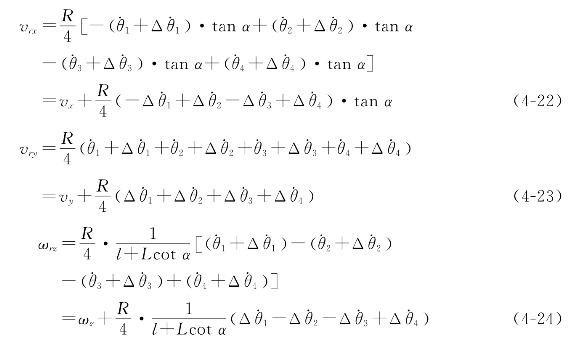
由上述几式可以看出,由于各个电机的转速误差,导致车辆在x、y和z三个自由度方向上均有误差。对于机器人x、y方向的运动,欲保持车辆直行的直线度,需满足
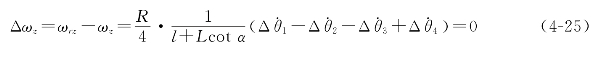
记机器人实际运行中(横向)x、(纵向)y之间的夹角为φ,取
![]()
则有
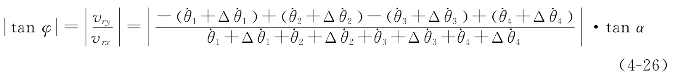
(1)当机器人向x轴负向运动时![]() ,有
,有
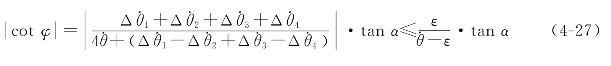
结合误差条件,有即
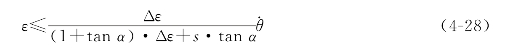
(2)当机器人向y轴正向运动时![]() 有
有

结合误差条件,有![]() 即
即
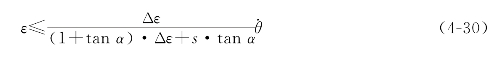
(3)当机器人向右前方运动时![]() ,有
,有
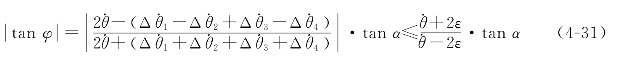
结合误差条件,有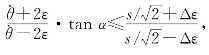 即
即
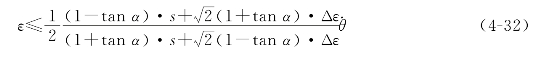
另外五个方向的分析与上述分析类同。
分别令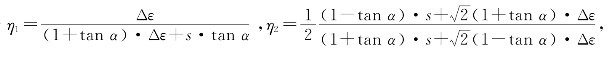 当α和期望位移s不同时,可得η1和η2的曲线如图4-5、图4-6。图中有线连接的表示η2,无线连接的表示η1。
当α和期望位移s不同时,可得η1和η2的曲线如图4-5、图4-6。图中有线连接的表示η2,无线连接的表示η1。
由图4-5可以看出,当允许位移误差确定,α也确定时,随着控制运动位移的增大,电机转速允许测量误差η1和η2均随之减小,也就是说,期望运动精度越高,电机转速允许测量误差越小;当允许位移误差确定,控制运动位移s也确定时,随着轮毂轴线与辊子轴线夹角α的增大,电机转速允许测量误差η1和η2均随之减小。对比图4-5和图4-6可以看出,当期望运动精度较低时,电机转速允许测量误差也随之增大。
α值不同,η1和η2对应的大小关系也不同,在α确定时,在一定的运动精度要求下,取![]() 为电机转速允许测量误差。据此,可以确定在保证精度的前提下,电机编码器的最大分辨率。
为电机转速允许测量误差。据此,可以确定在保证精度的前提下,电机编码器的最大分辨率。
本章所用Mecanum轮轮毂轴线和辊子轴线夹角α=42.47°,在位移误差Δε=1 mm,运动位移s=50 mm时,可得电机转速允许测量误差为2.3%,可选用100线以上的编码器进行转速测量。
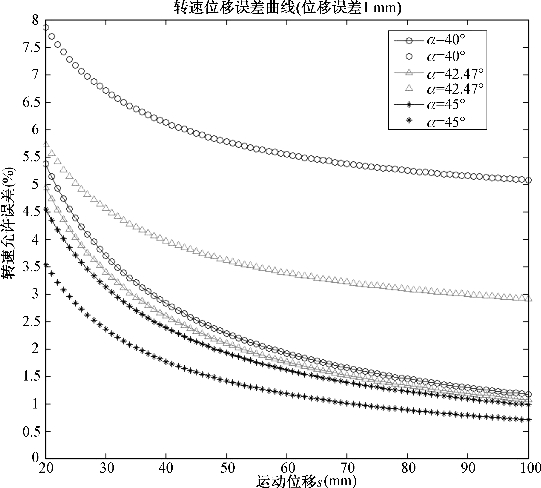
图4-5 Δε=1 mm时的转速位移误差曲线
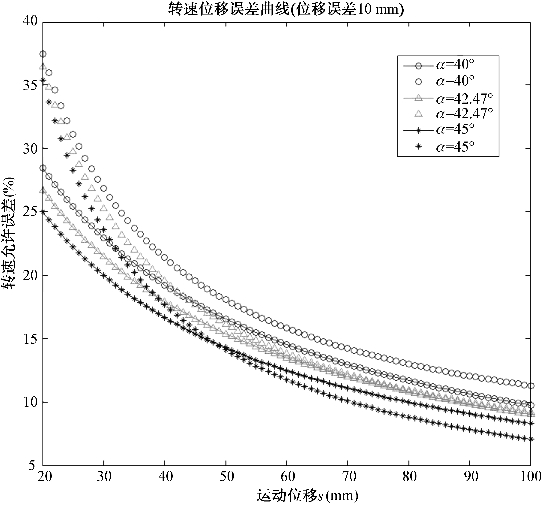
图4-6 Δε=10 mm时的转速位移误差曲线
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




