一个传统的自动控制系统包括以下几个方面:控制器、传感器、传动机构、执行机构、输入输出接口、控制对象等。而PID控制由于其算法结构简单、工作可靠、稳定性好、调整方便而成为控制器的主要控制方式之一,也是实际工业控制过程中应用最广泛、最成功的控制方法。PID控制实际上是对偏差信号进行比例、积分、微分运算之后形成的一种控制规律,其基本控制结构如图4-2所示。

图4-2 PID控制基本结构
由PID控制基本结构图可见,PID的控制性能的好坏主要取决于Kp、Ki、Kd三个控制参数的选择。其中,Kp为比例环节参数,当Kp>1时,开环增益加大,稳态误差减小,可以加快系统响应,但是随着Kp的增大,系统的稳定性变差;Ki为积分环节参数,加入积分控制可以增强系统的抗高频干扰能力,增加开环增益,减小稳态误差,但是纯积分环节会使相角滞后,故而不单独使用;Kd为微分控制参数,微分环节可以增大截止频率和相角裕度,减小调节时间和系统超调,提高系统快速性和平稳性,但其在增大截止频率的同时也放大了高频干扰,因此一般不单独使用。
由图4-2可以得到PID控制的一般控制算式:

取采样时间为Ts,则可将式(4-1)离散化(https://www.xing528.com)
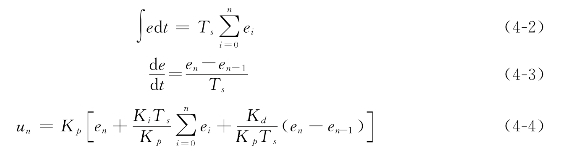
此即为位置型PID控制。
由式(4-4)可得,第(n-1)次采样有:
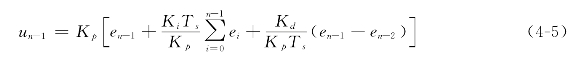
两式相减,得增量型PID控制算式:
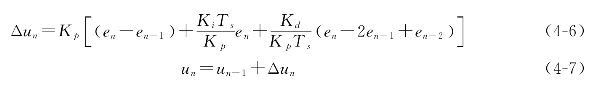
位置型PID控制算法需要对过去误差进行累加,计算量大,容易产生较大的累积误差,且输出为控制量的全部输出,误动作对系统的影响大;增量型PID控制算法得到的是控制增量,可以通过逻辑判断限制或者禁止本次输出,误动作影响小,计算量也较小,不易产生饱和积分,所以实际应用中增量型PID控制算法用得较多。本文所用PID算法即为增量型。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




