八主动Mecanum轮移动机器人全方位分析

如图3-5所示，八主动Mecanum轮全方位移动机器人的Mecanum轮被分成四组，每组两个Mecanum轮，假设两个轮子连接件的中点为轮子与机器人本体的悬挂点，那么整个机器人的运动速度是由两个轮子连接件中点的速度决定的。

在一组Mecanum轮中，两个Mecanum轮的姿态相同，如图3-6所示，

图3-6　组合Mecanum轮示意图

假设Mecanum轮的驱动电机的转速为ω，Mecanum轮转动的线速度为V，辊子的转动线速度为Vr，根据单个Mecanum轮的动力学分析可知，此时两个Mecanum轮的速度都为：

根据刚体运动学可以得出，整个连接件上任意一点的速度都和Mecanum轮的速度相同，所以八主动Mecanum轮全方位移动机器人的运动学和四轮Mecanum轮全方位移动机器人的运动学完全相同，动力学方程因Lagrange函数多了四个被动Mecanum轮转动的动能而有点小的差异，机器人的动力学方程为：

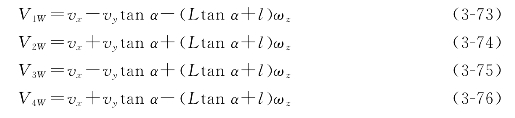
机器人三个自由度上的速度分别为：(https://www.xing528.com)

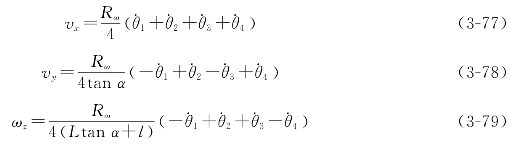
八主动Mecanum轮全方位移动机器人的系统动能包括：机器人因X方向和Y方向的速度产生的动能、机器人自身旋转的动能、八个主动轮绕其轴转动的动能。我们假定机器人在一个平面上运行，也就是说机器人的势能一直为一定值U，同时还有若干个正与地面接触或者刚与地面分离不久的辊子的转动动能Vg，从四轮Mecanum轮全方位移动机器人的动力学分析中可以看出，机器人势能和辊子转动的动能对机器人的动力学分析没有影响，可以忽略。所以，八主动Mecanum轮全方位移动机器人整个系统的Lagrange函数为：

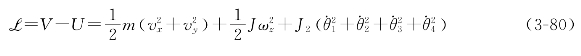
机器人在路面行驶的过程中，轮子与地面之间存在摩擦力，所以整个系统存在耗散力，假设轮子与地面之间的摩擦系数为μ，则整个系统的瑞利耗散函数R为：

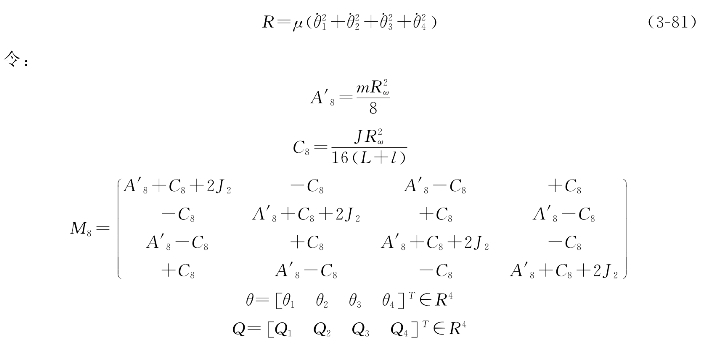
结合等式（3-51）～（3-54）、（3-55）～（3-57）、（3-73）和（3-22），八主动Mecanum轮全方位移动机器人的动力学方程为：

本章对两种典型布置的Mecanum轮全方位移动机器人的运动学进行了理论分析，在此基础上引入Lagrange动力学方程建立其动力学方程，在对四主动四被动Mecanum轮全方位移动机器人运动学和动力学分析基础上，对八主动Mecanum轮全方位移动机器人进行了分析，解析了不同布置方式下的运动情况。本章的内容为实现不同安装方式下的Mecanum轮全方位移动机器人的移动控制、提高其运动控制精度提供了理论基础。