悬架竖直放置的五自由度AGV智能运输车的垂向振动数学模型优化

建立了上述AGV智能运输车的垂向振动力学模型后，下面就需要建立相应的数学模型进行求解。目前来说，常用的数学建模方法一般分为两类：牛顿法和拉格朗日法。利用牛顿法求解时，需要考虑系统中各个质点受到的力的大小和方向，因此对于系统结构较为简单，简化后只有两三个自由度的力学模型，利用牛顿法可以得到较为简单的动力学微分方程。拉格朗日法不需要精确地知道各个质点的受力，只需要知道系统的功和能就可以得到系统的动力学模型，因此对于结构复杂和自由度较多的耦合系统更加方便。

本方案中的AGV智能运输车采用了悬架竖直安装方式来实现减振，将系统简化为空间五自由度的力学模型。鉴于AGV智能运输车振动系统的复杂性，对上述力学模型采用拉格朗日法建立数学模型。

1.五自由度AGV智能运输车的垂向振动能量

（1）AGV智能运输车的动能：

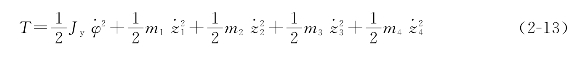
（2）AGV智能运输车的势能：

（3）AGV智能运输车的耗散能：

2.五自由度AGV智能运输车的垂向振动能量导数

（1）AGV智能运输车的动能对各个速度的导数：

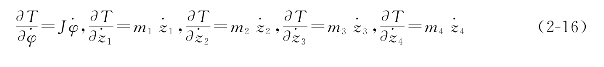
则：

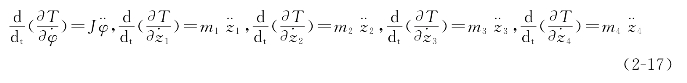
（2）AGV智能运输车的动能对各个位移的导数：

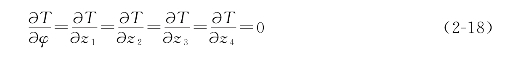
（3）AGV智能运输车的势能对各个位移的导数：

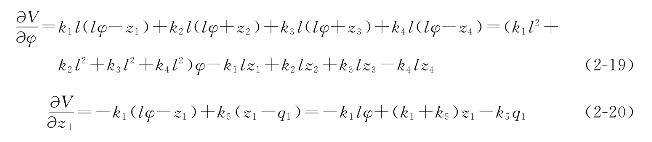
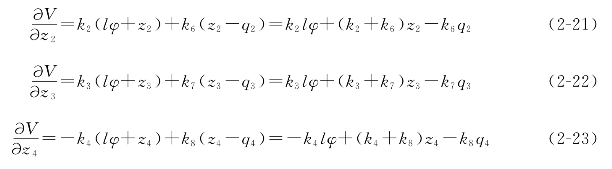
（4）AGV智能运输车的耗散能对各个速度的导数：

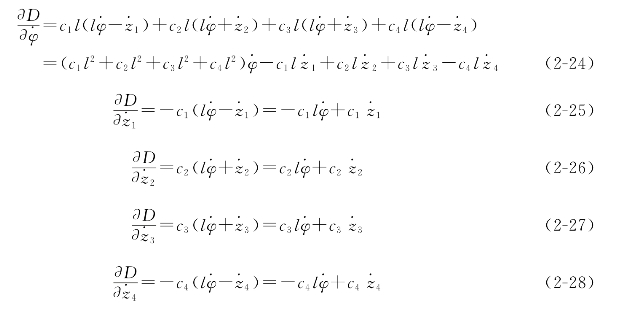
3.五自由度AGV智能运输车的垂向振动数学模型

对空间五自由度AGV智能运输车的垂向振动力学模型，运用第二类拉格朗日方程进行数学分析，方程如下：

式中：

T——系统的动能；

V——系统的势能；

D——系统的耗散能；

qi——系统的广义坐标。

将上节列出的2-13～2-28方程式，代入第二类拉格朗日方程，则：

(www.xing528.com)

将上述五个方程整理成矩阵表示为：

其中：

Q=[q1q2q3q4]T;

Z=[φ z1z2z3z4]T;

M——质量参数矩阵；

C——阻尼参数矩阵；

K——刚度参数矩阵；

Kt——聚氨酯刚度矩阵。

上述各个矩阵具体分别为：

质量参数矩阵：

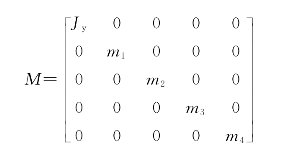
阻尼参数矩阵：

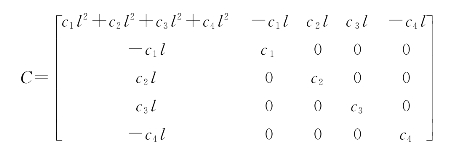
刚度参数矩阵：

路面激励对应的矩阵：

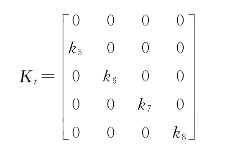
4.仿真分析

前述内容介绍的悬架竖直放置的五自由度AGV智能运输车垂向振动模型的质量矩阵、刚度矩阵、阻尼矩阵，为以后加入路面随机激励谱对不同弹簧阻尼值下的振动输出仿真提供了理论依据，这样就可以通过振动输出来优化弹簧阻尼系统。

假设所设计的AGV智能运输车左前轮受到地面0.03 m的垂向阶跃位移，则通过改变悬架系统中的弹簧刚度来看车身侧倾角的变化，如图2-40所示。当弹簧刚度取30 N/mm时，发现车身的侧倾角直接到最大值，之后趋于一个稳定值，没有弹性变化的过程，说明弹簧所取刚度偏大。当弹簧刚度取10 N/mm时，发现车身侧倾角直接突然很大，之后出现较长时间震荡，说明弹簧所取刚度偏小。相比较而言，当弹簧刚度取20 N/mm时，发现车身的侧倾角达到一个最大值，之后出现一个相对较短时间的震荡，最后趋于侧倾角较小的稳定状态，所以弹簧刚度取此值最合适。

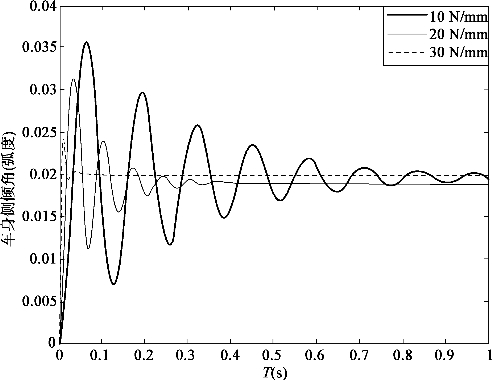
图2-40　改变弹簧刚度时车身侧倾角变化

从上述推导出来的AGV智能运输车的振动动力学方程可知，系统的非悬挂质量（包括Mecanum轮、电机、减速器等）也是影响系统振动的因素，因此对非悬挂质量分别取40 kg、60 kg和80 kg得出车身侧倾角变化，如图2-41所示。从图中可以看出当非悬挂质量取的较小时，车身振动情况最优，因此可以优化Mecanum轮质量来减少车体振动。

轮体振动也是造成AGV智能运输车车身振动的原因，为了定性分析轮体振动对AGV智能运输车车身振动的影响，假设所设计的AGV智能运输车左轮体受到0.03 m的垂向阶跃位移，则可以通过仿真得出车体振动情况，图2-42为AGV智能运输车车身侧倾角的变化。

Mecanum轮全方位移动机器人在运输货物的过程中产生振动是不可避免的，不仅路面的高低不平会引起Mecanum轮全方位移动机器人车体振动，而且Mecanum轮全方位移动机器人主要部件电机、减速器和车架的固有频率也是造成全方位移动机器人振动的原因。对于具有良好避振性能的全方位移动机器人可以保证货物在运输过程中不受损坏，延长移动机器人零件的疲劳寿命，同时减少车体振动可以增加它的控制精度，更好实现精确控制。

图2-41　改变非悬挂质量时车身侧倾角变化

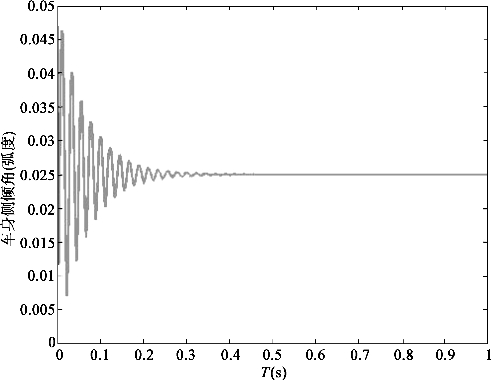
图2-42　轮体振动对车身侧倾角的影响

本章对Mecanum轮全方位移动机器人机构学进行相关分析和研究，详细解读了不同运动形式的Mecanum轮机器人的运动原理；介绍了Mecanum轮辊子和轮毂结构的参数化设计方法，并对设计软件进行了说明；针对Mecanum轮辊子弹性变形引起的车身振动问题，讨论了辊子刚度计算方法和抗震优化设计；对不同组合方式的Mecanum轮移动机器人车体悬架设计开展了动力学分析。