辊子和轮毂的参数优化设计方案

支撑方式不同，Mecanum轮的结构不同，但是主要的组成部分是相似的。图2-4是一种典型的两端支撑形式的Mecanum轮，图2-4中1为辊子，Mecanun轮的外观结构即一定数量的辊子均布在轮毂上；2为轮毂，用于在某固定的位置上固定辊子，因为开孔的位置与轮毂轴线成一定角度，所以轮毂的加工比较复杂；3为辊子的包胶外壁，为了减少地面带来的震动，辊子的金属内壁外面包了一层有一定厚度的橡胶或聚氨酯弹性体；4为辊子轴，通过两端的螺母固定在轮毂上；5为轴承，保证辊子平稳地转动。

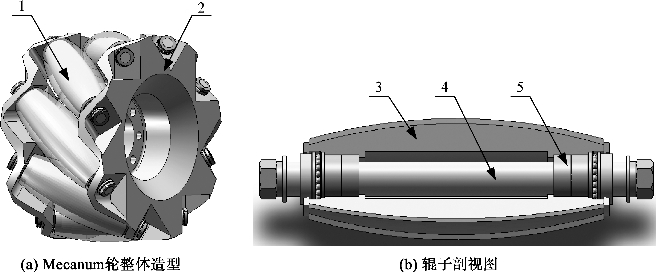
图2-4　两端支撑形式的Mecanum轮

辊子轮廓设计是Mecanum轮全方位移动机器人平稳运行的关键，要综合考虑轮子的运动连续性和重合度、轮轴高度一致性和平稳性、辊子轴的支承强度等。

1.辊子的参数设计

在Mecanum轮的结构设计中，最重要的是轮毂和辊子外轮廓线的设计。图2-5为Mecanum轮的正视图和侧视图，从图中可以看出，辊子的外轮廓在一个圆柱体的圆柱面上，所以我们使用下面的方法生成辊子的外轮廓线。

图2-5　两端支撑形式的Mecanum轮正视图和侧视图

如图2-6所示，B为圆柱体的高度，即Mecanum轮的理论宽度；R为圆柱体的半径，即轮子的半径；AA'为圆柱体表面的一条曲线，假设AA'是Mecanum轮辊子的外轮廓线，即轮子滚动时曲线AA'与地面接触。曲线AA'绕轴线AA'旋转即形成了辊子的外轮廓。C为曲线AA'上任意一点；θ为螺旋线AC绕Z轴的转角。假设曲线AA'为一条等速螺旋线，即当A点沿Z轴等速率运动时，也沿着顶面圆周等角速度旋转，则γ为螺旋线AA'绕Z轴的转角，所以有：

辊子的外轮廓线并不是图中所示的整段的等速螺旋线AA'，而是取螺旋线中间的一段。如图2-7所示，假设X轴为辊子的中心轴，DE段为实际的辊子的轮廓线，l为辊子的长度，δmin为辊子最小半径，δmax为辊子最大半径。

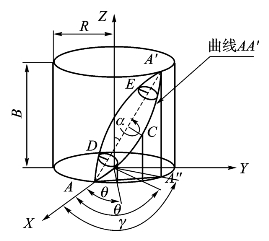
图2-6　辊子外轮廓线生成图

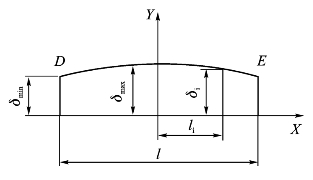
图2-7　辊子主要尺寸

Mecanum轮主要有以下几个比较重要的参数：

（1）辊子轴线与轮子轴线的夹角α；

（2）辊子最小端半径δmin，最大端半径δmax；

（3）辊子的长度l；

（4）辊子的数目N；(www.xing528.com)

（5）Mecanum轮的运动连续性系数ε；

（6）辊子轴线与Mecanum轮轴线的最小距离Smin。

设计Mecanum轮辊子的步骤如下：

首先根据载荷及机器人的整体结构估计Mecanum轮的半径R和宽度B，由式（2-1）计算得γ。由式（2-2）可计算得出辊轮轴线夹角α。

根据载荷计算得出轴承的尺寸，加上聚氨酯弹性体的厚度，可以得到辊子最小端的半径δmin，由式（2-2）利用牛顿迭代法或Matlab计算出θ0，θ0为辊子端点对应的θ角。将θ=γ/2代入式中，可得最大端半径δmax。

在已知R、γ和θ0的情况下，由式（2-4）可以计算出辊子的长度l。

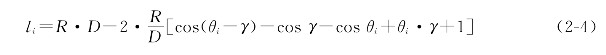
Mecanum轮的运动连续性系数ε定义为车轮旋转一圈，辊子与地面的接触线在圆柱面上的投影的长度与圆柱面的周长的比率，如式（2-5）所示。当ε≥1时，就可保证轮子是连续运动的。根据经验可得，一般ε取1.01～1.03，当其值太大时，辊子均布在轮毂上会发生干涉。由式（2-5）可以得出为了达到轮子连续运动的目的需要的辊子的数目N。

在对Mecanum轮进行建模时，因为辊子是均布在轮子的轴线周围的，所以需要知道辊轴线与轮轴线的最小距离Smin，由式（2-6）可计算得出。

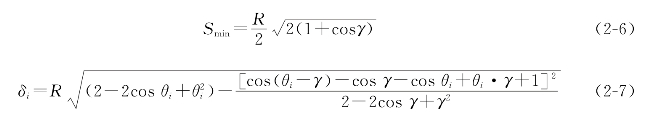
将辊子轮廓线等分为i等份，由式（2-4）和式（2-7）可计算得出图2-7中所示轮廓线任意点的δi值。进行轮廓线的简化，将相邻的端点以切线圆弧代替，形成辊子的轮廓线。等分的份数越多，拟合的轮廓线越贴近理论的轮廓线。在数控车床上加工时只需输入各段的坐标值及各段圆弧的半径，即可加工出辊子的外形。

2.轮毂的参数设计

轮毂采用一体化的设计，如图2-8所示。轮毂最重要的参数有：轮毂的宽度B，轮毂上安装辊子的孔的位置。这两个参数在上述计算过程中已经得到。

图2-8　Mecanum轮的轮毂

由以上的计算过程可知，辊子最小端的半径是决定Mecanum轮尺寸的最重要的因素。经过多次设计可以得出结论：在辊子最小端半径确定的情况下，辊子数目在7～9之间时，轮子的半径最小，此时的结构最优。