周转轮系传动比计算方法

在周转轮系中，由于行星轮的轴线是转动的，行星轮既有公转又有自转。因而不能直接用定轴轮系中简单的齿数比的方法计算两个回转轴之间的传动。

求解周转轮系传动比最常用的方法是转化机构法。其基本思想是，设法把周转轮系转化成定轴轮系，然后间接地利用定轴轮系的传动比公式来求解周转轮系的传动比。下面以图8－8所示的周转轮系为例，说明转化机构法的基本思想和计算方法。

如图8－8（a）所示的周转轮系中，设 ω1、ω2、ω3及 ωH分别表示齿轮 1、2、3及系杆 H 在周转轮系中的角速度。若给整个周转轮系加上一个与系杆H的角速度大小相等、方向相反的公共角速度－ωH后，系杆H的角速度变为零，即系杆H将变为静止不动，如图8－8（b）所示。根据相对运动原理，这样并不影响轮系中各构件之间的相对运动关系。此时，整个周转轮系便转化为一个假想的定轴轮系，称此假想的定轴轮系为原周转轮系的转化轮系。

图8－8　周转轮系及转化轮系

表8－1列出了转化前后各构件的角速度。表中所列转化轮系中各构件的角速度、和的右上方都标注有角标H，表示这些构件相对系杆H的角速度。

表8－1　转化前后各构件的角速度

既然周转轮系的转化轮系为一定轴轮系，因此转化轮系中输入和输出轴的传动可用定轴轮系传动比的计算方法求出，转向也用定轴轮系的判断方法来确定。如图8－8（b）所示转化轮系中齿轮1对齿轮3的传动比为

等式右边的“－”表示在转化轮系中轮1和轮3的转向相反。

将以上分析推广到一般情况。设nG和nK为周转轮系中任意两个齿轮G和K的转速，它们与行星架H的转速nH之间的关系为

应用上式时，G为主动轮（输入构件），K为从动轮（输出构件），中间各轮的主从地位应按这一个假定去判断。m为齿轮G至K间外啮合的对数。

应用式（8－2）时，应注意以下几点：

（1）nG、nK、nH必须是轴线平行或重合的齿轮或系杆的转速。其原因在于公式推导中，转速－nH与各构件原来的转速是代数相加的，因而nG、nK、nH必须是平行向量。因此，对于圆锥齿轮所组成的周转轮系（图8－9），其两中心轮间或中心轮与转臂之间的传动比，可应用式（8－2）计算，但行星轮的轴线与中心轮（或转臂）的轴线不平行，故行星轮的转速不能用上式计算。

（2）转速nG、nK、nH须将其大小和正、负号一并代入公式。在假定其中一已知转速的转向为正号之后，则另一已知转速的转向与其相同时取正号，与其相反取负号。对于行星轮系，固定中心轮的转速用“0”代入。(www.xing528.com)

例8－2　如图8－9所示圆锥齿轮的周转轮系中，已知齿轮齿数z1＝40，z3＝60，两中心轮同向回转，转速 n1＝100r/min，n3＝200r/min，求行星架 H 的转速 nH。

解　由式（8－2）得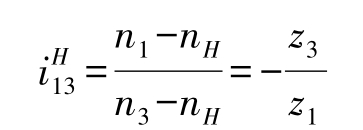

齿数比前的“－”号表示在转化轮系中，轮1和轮3转向相反。由题意知，轮1和轮3同向回转，故n1和n3以同号代入上式，则有

解得　nH＝160r/min

经计算nH为正，故nH与n1转向相同。

例8－3　如图8－10 所示的周转轮系，已知 z1＝100，z2＝101，z2'＝100，z3＝99，试求主动件H对从动件1的传动比iH1。

图8－9　圆锥齿轮差动轮系

图8－10　大传动比行星轮系

解　在图示轮系中，由于轮3为固定轮，即n3＝0，故轮系为行星轮系。传动比可根据式（8－2）求得

则

因此

即当转臂H转10000转时，轮1才转1转。其转向与转臂H的转向相同，可见轮系能获得很大的传动比。