两连架杆对应位置设计方法

如图3－38（a）所示，设已知四杆机构中两固定铰链A和D的位置、连架杆AB的长度，要求两连架杆的转角能实现如图三组对应关系，试设计平面四杆机构。

图3－37　炉门机构的设计

图3－38　按给定的两连架杆对应位置设计平面四杆机构

1.设计分析

连架杆CD上的铰链中心C位置未知，故连架杆CD的位置用其上的某一标线DE表示。设计此四杆机构的关键是求出铰链中心C的位置。

为此分析四杆机构ABCD的运动情况。当主动连架杆AB运动时，连杆上铰链B相对于另一连杆架CD的运动，是绕铰链点C的转动。则以C为圆心、BC长为半径的圆弧即为连杆上已知铰链点B相对于铰链C的运动轨迹。如能找到铰链B的这种轨迹，铰链C的位置即可确定。

根据相对运动原理，平面四杆机构改换机架，机构中各构件间的相对运动关系并不会改变。故确定C点位置可以假想DE（DC）为机架，AB为连杆，将原已知条件转化为给定连杆三位置的设计问题。

2.具体设计步骤如下

①取DE1为假想机架（也可取DE2或DE3），则AB为“连杆”；

②求出“连杆”AB上动铰链B相对于C1运动的三个位置。连接DB2E2和DB3E3成三角形（图3－38（b））并将其视为刚体，使上述两三角形绕铰链D分别反转（ψ1－ψ2）和（ψ1－ψ3）角度，即得和两点；

③作和的中垂线，其交点C1即为所求。AB1C1D即为要设计的四杆机构。

上述设计问题用解析法设计时，具体过程如下：

如图3－39所示的铰链四杆机构中，已知连架杆AB和CD应满足若干组对应位置φi、ψi，初始角为 φ0、ψ0。设计此四杆机构。

图3－39　给定连架杆四对位置

图3－40　机构封闭多边形

建立坐标系如图3－40所示，使x轴与机架重合，各构件以矢量表示，它们与x轴的夹角如图所示。各矢量在x和y轴上的投影有如下关系：(www.xing528.com)

取各构件长度的相对值，即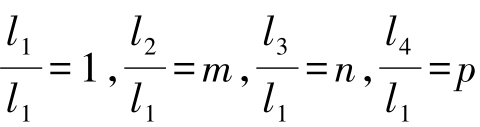，并移项，得

mcos δi＝p＋ncos(ψi＋ψ0)－cos(φi＋φ0)

msin δi＝nsin(ψi＋ψ0)－sin(φi＋φ0)

将上两式两边平方后相加，消去与设计无关的δi角，并整理得

令

则得

上式即为两连架杆转角之间的关系式。含有C0、C1、C2、φ0、ψ05个待定参数，因此最多只能给定连架杆五组对应角位置（i＝1、3、…、5）才有确定解。当n＝4时，有无穷多解，可选定一参数（φ0或ψ0），再求解方程组。当n＝3时，如给定φ0或ψ0，则解线性方程组可求出C0、C1、C2，进而求出m、n、p，最后根据实际需要给定某一构件的长度，这样其余构件长度也可确定。当n＝2时，在给定初始位置的基础上，再任意给定C0、C1、C2三个参数中的一个，即可求解，且有无穷多解。

由上述可知，当n＞3～5时，需借助计算机求解非线性方程组，实际工作中多采用优化逼近方法获得近似解。

下面介绍一种简便的近似设计方法——实验法。

如图 3－41（a）所示，已知两连架杆 1 和 3 之间的四对对应转角为 φ12、φ23、φ34、φ45和ψ12、ψ23、ψ34、ψ45，试设计四杆机构。

图3－41　实验法设计四杆机构

设计步骤如下：

①如图3－41（a）所示，任取连架杆AB的长度l1，画出其已知的位置，得到AB1、AB2、AB3、AB4和 AB5。再任取连杆 BC 的长度 l2，分别以 B1、B2、B3、B4和 B5为圆心、l2为半径画弧，得圆弧 K1、K3、K3、K4 和 K5。

②另如图3－41（b）所示，在透明纸上画出连架杆CD的给定位置，得到Dd1、Dd2、Dd3、Dd4和Dd5，再以D为圆心作出若干个同心圆弧。

③将透明纸放在图3－41（a）上，移动透明纸，使其上的某一同心圆弧与连架杆CD的各给定位置的交点 C1、C2、C3、C4和 C5分别近似落在弧 K1、K2、K3、K4和 K5上。则 AB1C1D 即为所求的四杆机构。如果交点C2不能落在弧K2上，或误差较大，可改变连杆长l2和连架杆长l1，重试直到获得满意的结果。