单位四元数：定义、性质与应用

（1）四元数定义。四元数是对复数的一种扩展，或叫超复数。记作一个标量加上一个向量，即

其中s ∈R，v ∈R3，正交复数i、j、k 定义如下，即

i2 + j2 + k2= ijk=-1

因此，一个四元数表示为：。

（2）单位四元数的定义。为了描述坐标系的旋转，单位四元数的表示为 或。

单位四元数可以被看作绕单位向量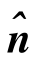旋转了角度θ，该旋转于四元数组的关系为

（3）四元数与旋转的关系。由此而知复数中，乘以i 相当于对向量旋转了90°；在四元数中乘以i 相当于对向量旋转了180°，旋转360°结果为“-1”，旋转720°表示回到原来的姿态。

假设某个旋转是绕单位向量n=（nx，ny，nz）T 旋转了θ 角，那么，这个旋转的四元数形式为 。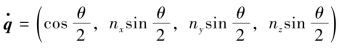

例如，ABB RAPID 语言采用四元数定义工具姿态，具体过程如下。

①数值定义：四元数的数值采用如下公式计算。

其中，（x1，x2，x3），（y1，y2，y3），（z1，z2，z3）分别是旋转坐标系统X′、Y′、Z′轴单位向量在基准坐标系X、Y、Z 轴上的投影。

②符号定义：

：符号总为正；(www.xing528.com)

：符号与y3 -z2 的计算结果相同；

：符号与z1 -x3 的计算结果相同；

：符号与x2 -y1 的计算结果相同。

假设机器人工具坐标系围绕基准坐标系Y 轴逆时针旋转30°，则旋转坐标系X′、Y′、Z′轴单位向量在基准坐标系X、Y、Z 轴上的投影分别为

(x1,x2,x3)=(cos 30°,0,-sin 30°)

(y1,y2,y3)=(0,-1,0)

(z1,z2,z3)=(sin 30°,0,cos 30°)

由此可得

所以，其四元数为（0.966，0，0.259，0）。

此外，还可以根据公式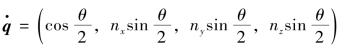直接进行计算：n=（nx，ny，nz）=（0，1，0），θ=30°，结算结果相同。

与复数一样，可以用四元数表达对一个空间点的旋转，P=（x，y，z）∈R3，由轴角指定旋转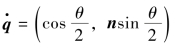，旋转后的点。